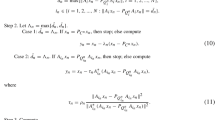Skip to main content
SpringerLink
Log in

Self-adaptive algorithms for solving split feasibility problem with multiple output sets

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

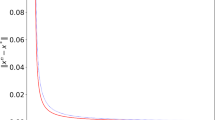
In this paper, we study the split feasibility problem with multiple output sets in Hilbert spaces. For solving the aforementioned problem, we propose two new self-adaptive relaxed CQ algorithms which involve computing of projections onto half-spaces instead of computing onto the closed convex sets, and it does not require calculating the operator norm. We establish a weak and a strong convergence theorems for the proposed algorithms. We apply the new results to solve some other problems. Finally, we present some numerical examples to show the efficiency and accuracy of our algorithm compared to some existing results. Our results extend and improve some existing methods in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Censor, Y., Elfving, T.: A multiprojection algorithm using bregman projections in a product space. Numer. Algorithms 8(2), 221–239 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  2. Byrne, C.: Iterative oblique projection onto convex sets and the split feasibility problem. Inverse Probl. 18(2), 441 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  3. Censor, Y., Elfving, T., Kopf, N., Bortfeld, T.: The multiple-sets split feasibility problem and its applications for inverse problems. Inverse Probl. 21(6), 2071 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  4. Censor, Y., Bortfeld, T., Martin, B., Trofimov, A.: A unified approach for inversion problems in intensity-modulated radiation therapy. Phys. Med. Biol. 51(10), 2353 (2006)

    Article  Google Scholar 

  5. Censor, Y., Segal, A.: Iterative projection methods in biomedical inverse problems. Mathematical methods in biomedical imaging and intensity-modulated radiation therapy (IMRT) 10, 65–96 (2008)

    MathSciNet  Google Scholar 

  6. Wang, J., Hu, Y., Li, C., Yao, J.-C.: Linear convergence of CQ algorithms and applications in gene regulatory network inference. Inverse Probl. 33 (5), 055017 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  7. Ansari, Q. H., Rehan, A.: Split feasibility and fixed point problems. In: Nonlinear Analysis, Springer, pp. 281–322 (2014)

  8. Xu, H.-K.: Iterative methods for the split feasibility problem in infinite-dimensional hilbert spaces. Inverse Probl. 26(10), 105018 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  9. Byrne, C.: A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 20(1), 103 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  10. Takahashi, W.: The split feasibility problem and the shrinking projection method in banach spaces. J. Nonlinear Convex Anal. 16(7), 1449–1459 (2015)

    MathSciNet  MATH  Google Scholar 

  11. Xu, H.-K.: A variable krasnosel’skii–mann algorithm and the multiple-set split feasibility problem. Inverse Probl. 22(6), 2021 (2006)

    Article  MATH  Google Scholar 

  12. Yang, Q.: The relaxed CQ algorithm solving the split feasibility problem. Inverse Probl. 20(4), 1261 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  13. Gibali, A., Mai, D. T., et al.: A new relaxed CQ algorithm for solving split feasibility problems in hilbert spaces and its applications. J. Ind. Manag. Optim. 15(2), 963 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  14. Sahu, D.R., Cho, Y.J., Dong, Q.L., Kashyap, M.R., Li, X.H.: Inertial relaxed CQ algorithms for solving a split feasibility problem in hilbert spaces. Numer. Algorithms 1–21 (2020)

  15. López, G., Martín-Márquez, V., Wang, F., Xu, H.-K.: Solving the split feasibility problem without prior knowledge of matrix norms. Inverse Probl. 28(8), 085004 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  16. He, S., Zhao, Z.: Strong convergence of a relaxed CQ algorithm for the split feasibility problem. J. Inequal. Appl. 2013(1), 197 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  17. Yao, Y., Postolache, M., Liou, Y.-C.: Strong convergence of a self-adaptive method for the split feasibility problem. Fixed Point Theory and Applications 2013(1), 201 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  18. Dang, Y., Sun, J., Xu, H.: Inertial accelerated algorithms for solving a split feasibility problem. Journal of Industrial and Management Optimization 13(3), 1383–1394 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  19. Gibali, A., Liu, L.-W., Tang, Y.-C.: Note on the modified relaxation CQ algorithm for the split feasibility problem. Optim. Lett. 12(4), 817–830 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  20. Zhang, W., Han, D., Li, Z.: A self-adaptive projection method for solving the multiple-sets split feasibility problem. Inverse Probl. 25(11), 115001 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  21. Zhao, J., Yang, Q.: A simple projection method for solving the multiple-sets split feasibility problem. Inverse Probl. Sci. Eng. 21(3), 537–546 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  22. López, G., Martin, V., Xu, H.K., et al.: Iterative algorithms for the multiple-sets split feasibility problem. Biomed. Math.: Promising Directions in Imag, Therapy Planning Inverse Problems 243–279 (2009)

  23. Dang, Y.-, Yao, J., Gao, Y.: Relaxed two points projection method for solving the multiple-sets split equality problem. Numer. Algorithms 78 (1), 263–275 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  24. Iyiola, O.S., Shehu, Y.: A cyclic iterative method for solving multiple sets split feasibility problems in banach spaces. Quaest. Math. 39(7), 959–975 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  25. Shehu, Y.: Strong convergence theorem for multiple sets split feasibility problems in banach spaces. Numer. Funct. Anal. Optim. 37(8), 1021–1036 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  26. Suantai, S., Pholasa, N., Cholamjiak, P.: Relaxed CQ algorithms involving the inertial technique for multiple-sets split feasibility problems. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas 113(2), 1081–1099 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  27. Wang, J., Hu, Y., Yu, C. K. W., Zhuang, X.: A family of projection gradient methods for solving the multiple-sets split feasibility problem. J. Optim. Theory Appl. 183(2), 520–534 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  28. Mewomo, O.T., Ogbuisi, F.U.: Convergence analysis of an iterative method for solving multiple-set split feasibility problems in certain banach spaces. Quaest. Math. 41(1), 129–148 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  29. Buong, N., Hoai, P. T. T., Binh, K. T.: Iterative regularization methods for the multiple-sets split feasibility problem in hilbert spaces. Acta Appl. Math. 165(1), 183–197 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  30. Yao, Y., Postolache, M., Zhu, Z.: Gradient methods with selection technique for the multiple-sets split feasibility problem. Optimization (2019)

  31. Wang, X.: Alternating proximal penalization algorithm for the modified multiple-sets split feasibility problems. J. Inequal. Appl. 2018(1), 1–8 (2018)

    Article  MathSciNet  Google Scholar 

  32. Taddele, G. H., Kumam, P., Gebrie, A. G., Sitthithakerngkiet, K.: Half-space relaxation projection method for solving multiple-set split feasibility problem. Math. Comput. Appl. 25(3), 47 (2020)

    MathSciNet  Google Scholar 

  33. Taddele, G. H., Kumam, P., Gebrie, A. G.: An inertial extrapolation method for multiple-set split feasibility problem. J. Inequal. Appl. 2020 (1), 1–22 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  34. Sunthrayuth, P., Tuyen, T. M.: A generalized self-adaptive algorithm for the split feasibility problem in banach spaces. Bull. Iran. Math. Soc. 1–25 (2021)

  35. Censor, Y., Segal, A.: The split common fixed point problem for directed operators. J. Convex Anal 16(2), 587–600 (2009)

    MathSciNet  MATH  Google Scholar 

  36. Moudafi, A.: The split common fixed-point problem for demicontractive mappings. Inverse Probl. 26(5), 055007 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  37. Censor, Y., Gibali, A., Reich, S.: Algorithms for the split variational inequality problem. Numer. Algorithms 59(2), 301–323 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  38. Byrne, C., Censor, Y., Gibali, A., Reich, S.: The split common null point problem. J. Nonlinear Convex Anal 13(4), 759–775 (2012)

    MathSciNet  MATH  Google Scholar 

  39. Tuyen, T. M., Ha, N. S., Thuy, N. T. T.: A shrinking projection method for solving the split common null point problem in banach spaces. Numer. Algorithms 81(3), 813–832 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  40. Reich, S., Tuyen, T. M.: Two projection algorithms for solving the split common fixed point problem. J. Optim. Theory Appl. 186(1), 148–168 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  41. Reich, S., Tuyen, T. M.: Two new self-adaptive algorithms for solving the split common null point problem with multiple output sets in hilbert spaces. J. Fixed Point Theory Appl. 23(2), 1–19 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  42. Reich, S., Tuyen, T. M.: Projection algorithms for solving the split feasibility problem with multiple output sets. J. Optim. Theory Appl. 190(3), 861–878 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  43. Reich, S., Truong, M. T., Mai, T. N. H.: The split feasibility problem with multiple output sets in hilbert spaces. Optim. Lett 1–19 (2020)

  44. Bauschke, H. H., Combettes, P. L., et al.: Convex analysis and monotone operator theory in hilbert spaces, vol. 408. Springer, Berlin (2011)

    Book  MATH  Google Scholar 

  45. Goebel, K., Simeon, R.: Uniform convexity, hyperbolic geometry, and nonexpansive mappings. Dekker (1984)

  46. Opial, Z.: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 73(4), 591–597 (1967)

    Article  MathSciNet  MATH  Google Scholar 

  47. Rockafellar, R. T.: Monotone operators and the proximal point algorithm. SIAM journal on control and optimization 14(5), 877–898 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  48. Cholamjiak, P., Suantai, S., et al.: A new CQ algorithm for solving split feasibility problems in hilbert spaces. Bull. Malays. Math. Sci. Soc. 42 (5), 2517–2534 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  49. Maingé, P.-E.: Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization. Set-Valued Analysis 16(7-8), 899–912 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  50. Xu, H.-K.: Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 66(1), 240–256 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  51. Fukushima, M.: A relaxed projection method for variational inequalities. Math. Program. 35(1), 58–70 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  52. Reich, S., Tuyen, T. M.: Iterative methods for solving the generalized split common null point problem in hilbert spaces. Optimization 69(5), 1013–1038 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  53. Reich, S., Tuyen, T. M., Ha, M. T. N.: An optimization approach to solving the split feasibility problem in hilbert spaces. J. Glob. Optim 1–16 (2020)

  54. Cegielski, A.: Iterative methods for fixed point problems in hilbert spaces, vol. 2057. Springer, Berlin (2012)

    MATH  Google Scholar 

  55. Jeffs, B. D., Gunsay, M.: Restoration of blurred star field images by maximally sparse optimization. IEEE Trans. Image Process. 2(2), 202–211 (1993)

    Article  Google Scholar 

  56. Fevrier, I. J., Gelfand, S. B., Fitz, M. P.: Reduced complexity decision feedback equalization for multipath channels with large delay spreads. IEEE Trans. Commun. 47(6), 927–937 (1999)

    Article  Google Scholar 

  57. Duttweiler, D. L.: Proportionate normalized least-mean-squares adaptation in echo cancelers. IEEE Transactions on speech and audio processing 8(5), 508–518 (2000)

    Article  Google Scholar 

  58. Ramsey, J. B., Zhang, Z.: The application of wave form dictionaries to stock market index data. In: Predictability of complex dynamical systems, Springer, pp. 189–205 (1996)

  59. Halmos, P. R.: A hilbert space problem book. Springer-Verlag, New York (1982)

    Book  MATH  Google Scholar 

Download references

Acknowledgements

The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT. Guash Haile Taddele is supported by the Petchra Pra Jom Klao Ph.D. Research Scholarship from King Mongkut’s University of Technology Thonburi (Grant No.37/2561). Moreover, we would like to thank the Editor and Reviewers for taking the time and effort necessary to review the manuscript. We sincerely appreciate all valuable comments and suggestions, which helped us to improve the quality of the manuscript.

The authors acknowledge the financial support provided by “Mid-Career Research Grant” (N41A640089).

Funding

This research was funded by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), Faculty of Science, KMUTT. The first author was supported by the Petchra Pra Jom Klao Ph.D. Research Scholarship from King Mongkut’s University of Technology Thonburi with Grant No. 37/2561.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), 126 Pracha Uthit Rd., Bang Mod, Thung Khru, Bangkok, 10140, Thailand

    Guash Haile Taddele

  2. Center of Excellence in Theoretical and Computational Science (TaCS-CoE), Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), 26 Pracha Uthit Rd., Bang Mod, Thung Khru, Bangkok, 10140, Thailand

    Poom Kumam

  3. Department of Mathematics and Computer Science, Faculty of Science and Technology, Rajamangala University of Technology Thanyaburi (RMUTT), Thanyaburi, Pathumthani, 12110, Thailand

    Pongsakorn Sunthrayuth

  4. Department of Mathematics, College of Computational and Natural Science, Debre Berhan University, Debre Berhan, PO. Box 445, Ethiopia

    Anteneh Getachew Gebrie

  5. Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, 40402, Taiwan

    Poom Kumam

Authors
  1. Guash Haile Taddele
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Poom Kumam
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Pongsakorn Sunthrayuth
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Anteneh Getachew Gebrie
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Poom Kumam.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Author contribution

All authors contributed equally to the manuscript and read and approved the final manuscript.

Availability of data and material

Not applicable.

Code availability

Not available.

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Taddele, G.H., Kumam, P., Sunthrayuth, P. et al. Self-adaptive algorithms for solving split feasibility problem with multiple output sets. Numer Algor 92, 1335–1366 (2023). https://doi.org/10.1007/s11075-022-01343-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-022-01343-6

Keywords

Mathematics Subject Classification 2010

Search

Navigation