Skip to main content
SpringerLink
Log in

Fractional-order Chelyshkov wavelet method for solving variable-order fractional differential equations and an application in variable-order fractional relaxation system

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

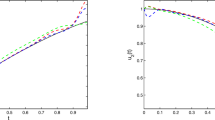
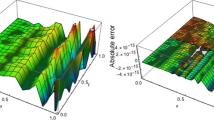
We give an efficient numerical approach to solve variable-order fractional differential equations (VO-FDEs) by applying fractional-order generalized Chelyshkov wavelets (FOGCW). The beta function is used to determine the exact value for the Riemann-Liouville fractional integral operator of the FOGCW. The exact value and the given wavelets are used to solve the VO-FDEs. Six examples are included to demonstrate the effectiveness of this method. In the last example, we show the application of our method to the variable-order fractional relaxation model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Levy, D.: Introduction to Numerical Analysis. Depart. Math. Maryland University, CSCAMM (2010)

    Google Scholar 

  2. Oldham, K.B.: Fractional differential equations in electrochemistry. Adv. Eng. Softw. 41(1), 9–12 (2010)

    Article  MATH  Google Scholar 

  3. Wong, J., Abilez, O.J., Kuhl, E.: Computational optogenetics: A novel continuum framework for the photoelectrochemistry of living systems. J. Mech. Phys. Solids. 60(6), 1158–1178 (2012)

    Article  Google Scholar 

  4. Zaky, M.A., Machado, J.A.T.: On the formulation and numerical simulation of distributed-order fractional optimal control problems. Commun. Nonlinear Sci. Numer. Simul. 52, 177–189 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  5. Naber, M.: Distributed order fractional sub-diffusion. Fractals 12(1), 23–32 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  6. Meerschaert, M.M., Nane, E., Vellaisamy, P.: Distributed-order fractional diffusions on bounded domains. J. Math. Anal. Appl. 379(1), 216–228 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  7. Agarwal, R.P.: Dynamical Systems and Applications. World Scientific (1995)

  8. Atanackovic, T.M., Pilipovic, S., Zorica, D.: Distributed-order fractional wave equation on a finite domain: Creep and forced oscillations of a rod. Conti. Mech. Thermodyna 23(4), 305–318 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  9. Kot, M.: Elements of Mathematical Ecology. Cambridge University Press (2001)

  10. Meng, X., Chen, L., Wu, B.: A delay sir epidemic model with pulse vaccination and incubation times. Nonlinear. Anal. Real. World. Appl. 11(1), 88–98 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  11. Wang, W., Lin, C.: A new algorithm for integral of trigonometric functions with mechanization. Appl. Math. Comput. 164(1), 71–82 (2005)

    MathSciNet  MATH  Google Scholar 

  12. Dehghan, M., Shakeri, F.: Solution of parabolic integro-differential equations arising in heat conduction in materials with memory via he’s variational iteration technique. Int. J. Numer. Method. Biomed. Eng. 26(6), 705–715 (2010)

    MathSciNet  MATH  Google Scholar 

  13. Jerri, A.: Introduction to Integral Equations with Applications. Wiley (1999)

  14. Patnaik, S., Hollkamp, J.P., Semperlotti, F.: Applications of variable-order fractional operators: A review. Proc. R. Soc. A 476(2234), 20190498 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  15. Glöckle, W.G., Nonnenmacher, T.F.: A fractional calculus approach to self-similar protein dynamics. Biophys. J. 68, 46–53 (1995)

    Article  Google Scholar 

  16. Sun, H.G., et al.: A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems. E.J.P.S.T. 193. 1, 185–192 (2011)

    Google Scholar 

  17. Coimbra, C.: Mechanics with variable-order differential operators. Ann. Phys. 12, 692–703 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  18. Chechkin, A.V., Gorenflo, R., Sokolov, I.M.: Fractional diffusion in inhomogeneous media. J. Phys. A.: Math. Gen. 38(42), 679 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  19. Sun, H., Chen, W., Chen, Y.: Variable-order fractional differential operators in anomalous diffusion modeling. Physica A Stat. Mech. Appl. 388, 4586–4592 (2009)

    Article  Google Scholar 

  20. Usman, M., Hamid, M., Haq, R.U., Wang, W.: An efficient algorithm based on Gegenbauer wavelets for the solutions of variable-order fractional differential equations. Eur. Phys. J. Plus. 133(8), 327 (2018)

    Article  Google Scholar 

  21. Chen, Y.M., Wei, Y.Q., Liu, D.Y., Yu, H.: Numerical solution for a class of nonlinear variable order fractional differential equations with legendre wavelets. Appl. Math. Lett. 46, 83–88 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  22. Heydari, M.H., Avazzadeh, Z., Haromi, M.F.: A wavelet approach for solving multi-term variable-order time fractional diffusion-wave equation. Appl. Math. Comput. 341, 215–228 (2019)

    MathSciNet  MATH  Google Scholar 

  23. Yuttanan, B., Razzaghi, M.: Legendre wavelets approach for numerical solutions of distributed order fractional differential equations. Appl. Math. Model. 70, 350–364 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  24. Ur Rehman, M., Khan, R.A.: The legendre wavelet method for solving fractional differential equations. Commun. Nonlinear. Sci. Numer. Simul. 16(11), 4163–4173 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  25. Li, Y.: Solving a nonlinear fractional differential equation using Chebyshev wavelets. Commun. Nonlinear. Sci. Numer. Simul. 15(9), 2284–2292 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  26. Akyüz-Daşcıoğlu, A., Sezer, M.: Chebyshev polynomial solutions of systems of higher-order linear Fredholm–Volterra integro-differential equations. J. Franklin Institute 342(6), 688–701 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  27. Phan, T.T., Vo, N.T., Razzaghi, M.: Taylor wavelet method for fractional delay differential equations. Eng. Comput., 1–10 (2019)

  28. Vichitkunakorn, P., Vo, T.N., Razzaghi, M.: A numerical method for fractional pantograph differential equations based on Taylor wavelets. T. I. Meas Control 42, 1334–1344 (2020)

    Article  Google Scholar 

  29. Keshavarz, E., Ordokhani, Y., Razzaghi, M.: Bernoulli wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Model. 38(24), 6038–6051 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  30. Oguz, C., Sezer, M.: Chelyshkov collocation method for a class of mixed functional integro-differential equations. Appl. Math. Comput. 259, 943–954 (2015)

    MathSciNet  MATH  Google Scholar 

  31. Moradi, L., Mohammadi, F., Baleanu, D.: A direct numerical solution of time-delay fractional optimal control problems by using Chelyshkov wavelets. J. Vib. Control 25(2), 310–324 (2019)

    Article  MathSciNet  Google Scholar 

  32. Ghoreishi, F., Yazdani, S.: An extension of the spectral Tau method for numerical solution of multi-order fractional differential equations with convergence analysis. Comput. Math. Appl. 61, 30–43 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  33. Mohammadi, F., Cattani, C.: Fractional-order Legendre wavelet Tau method for solving fractional differential equations. J. Comput. Appl. Math. 339, 306–316 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  34. Kazem, S., Abbasbandy, S., Kumar, S.: Fractional-order Legendre functions for solving fractional-order differential equations. Appl. Math. Model. 37(7), 5498–5510 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  35. Bhrawy, A.H., Alhamed, A.Y., Baleanu, D.: New spectral techniques for systems of fractional differential equations using fractional-order generalized Laguerre orthogonal functions. Fract. Calc. Appl. Anal. 17, 1138–1157 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  36. Rahimkhani, P., Ordokhani, Y., Babolian, E.: Fractional-order Bernoulli wavelets and their applications. Appl. Math. Model. 40, 8087–8107 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  37. Mashayekhi, S., Razzaghi, M.: Numerical solution of the fractional Bagley-Torvik equation by using hybrid functions approximation. Math. Methods. Appl. Sci. 39(3), 353–365 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  38. Mashayekhi, S., Razzaghi, M.: Numerical solution of distributed order fractional differential equations by hybrid functions. J Comput. Phys. 315, 169–181 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  39. Nagy, A.M., Sweilam, N.H., El-Sayed, A.A.: New operational matrix for solving multiterm variable order fractional differential equations. J. Comput. Nonlinear. Dyn., 13(1) (2018)

  40. Razminia, A., Dizaji, A.F., Majd, V.J.: Solution existence for non-autonomous variable-order fractional differential equations. Math. Comput. Model. 55(3–4), 1106–1117 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  41. Xu, Y., He, Z.: Existence and uniqueness results for Cauchy problem of variable-order fractional differential equations. J. Appl. Math. Comput. 43(1), 295–306 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  42. Zheng, X., Wang, H., Fu, H.: Well-posedness of fractional differential equations with variable-order Caputo-Fabrizio derivative. Chaos, Solitons & Fractals 138, 109966 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  43. Abramowitz, M., Stegun, I.A.: Handbook of Mathematical Functions. Dover (1973)

  44. Chelyshkov, V.S.: Alternative orthogonal polynomials and quadratures. Elect. Trans. Numer. Anal. 25(7), 17–26 (2006)

    MathSciNet  MATH  Google Scholar 

  45. Mohammadi, F.: Numerical solution of systems of fractional delay differential equations using a new kind of wavelet basis. Comput. Appl. Math. 37 (4), 4122–4144 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  46. Ngo, H.T.B., Vo, T.N., Razzaghi, M.: An effective method for solving nonlinear fractional differential equations. Engineering with Computers. https://doi.org/10.1007/s00366-020-01143-3 (2020)

  47. Bhrawy, A.H., Zaky, A.M.: Numerical algorithm for the variable-order Caputo fractional functional differential equation. Nonlinear. Dyn. 85 (3), 1815–1823 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  48. Hassani, H., Dahaghin, M.S., Heydari, H.: A new optimized method for solving variable-order fractional differential equation. J. Math. Ext. 11, 85–98 (2017)

    MathSciNet  MATH  Google Scholar 

  49. Zaky, M.A., et al.: New recursive approximations for variable-order fractional operators with applications. arXiv:1804.01198 (2018)

  50. Sun, H.G., Chen, W., Wei, H., Chen, Y.Q.: A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems. Eur. Phys. J. 193(1), 185–192 (2011)

    Google Scholar 

Download references

Acknowledgements

A part of this paper was completed when the corresponding author was working as a researcher at Vietnam Institute for Advance Study in Mathematics (VIASM). The author would like to thank the VIASM for providing a fruitful research environment and extending support and hospitality during their visit. The authors wish to express their sincere thanks to the anonymous referee for valuable suggestions that improved the final version of the manuscript.

Author information

Authors and Affiliations

  1. Fractional Calculus, Optimization and Algebra Research Group, Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Hoa T. B. Ngo & Thieu N. Vo

  2. Department of Mathematics and Statistics, Mississippi State University, Starkville, USA

    Mohsen Razzaghi

Authors
  1. Hoa T. B. Ngo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohsen Razzaghi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Thieu N. Vo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Thieu N. Vo.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ngo, H.T.B., Razzaghi, M. & Vo, T.N. Fractional-order Chelyshkov wavelet method for solving variable-order fractional differential equations and an application in variable-order fractional relaxation system. Numer Algor 92, 1571–1588 (2023). https://doi.org/10.1007/s11075-022-01354-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-022-01354-3

Keywords

Search

Navigation