Unconditionally optimal H¹-error estimate of a fast nonuniform L2-1_σ scheme for nonlinear subdiffusion equations

Abstract

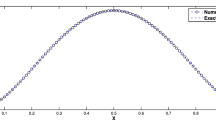
This paper is concerned with the unconditionally optimal H¹-error estimate of a fast second-order scheme for solving nonlinear subdiffusion equations on the nonuniform mesh. We use the Galerkin finite element method (FEM) to discretize the spacial direction, the Newton linearization method to approximate the nonlinear term and the sum-of-exponentials (SOE) approximation to speed up the evaluation of Caputo derivative. Our analysis of the unconditionally optimal H¹-error estimate involves the temporal-spatial error splitting approach, an improved discrete fractional Grönwall inequality and error convolution structure. In order to find a suitable test function to estimate H¹-error, we here consider two cases: linear and high-order FEM space, using the time-discrete operator and Laplace operator in the test function respectively. Numerical tests are provided demonstrate the effectiveness and the unconditionally optimal H¹-error convergence of our scheme.

Appendix: . The proof of Lemma 3.4

Proof 4

By the Taylor expansion, we obtain

$$ \begin{array}{@{}rcl@{}} R_{f}^{k-\sigma}&=&{\int}_{v^{k-1}}^{v^{k-\sigma}}(v^{k-\sigma}-\mu)f^{\prime\prime}(\mu) \mathrm{d} \mu\\ &=&{{\int}_{0}^{1}}\left[v^{k-\sigma}-v^{k-1}-s(v^{k-\sigma}-v^{k-1})\right]f^{\prime\prime}\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right)(v^{k-\sigma}-v^{k-1}) \mathrm{d} s\\ &=&(1-\sigma)^{2}(v^{k}-v^{k-1})^{2}{{\int}_{0}^{1}}(1-s)f^{\prime\prime}\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right) \mathrm{d} s,\\ \nabla R_{f}^{k-\sigma}&=&(1-\sigma)^{2}(v^{k}-v^{k-1})^{2}{{\int}_{0}^{1}}(1-s)f^{\prime\prime\prime}\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right)\nabla\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right) \mathrm{d} s\\ &&\quad+2(1-\sigma)^{2}(v^{k}-v^{k-1})\nabla(v^{k}-v^{k-1}){{\int}_{0}^{1}}(1-s)f^{\prime\prime}\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right) \mathrm{d} s,\\ {\Delta} R_{f}^{k-\sigma}&=&2(1-\sigma)^{2}(v^{k}-v^{k-1})\nabla(v^{k}-v^{k-1}){{\int}_{0}^{1}}(1-s)f^{\prime\prime\prime}\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right)\\ &&\quad\quad\nabla\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right) \mathrm{d}s\\ &&\quad+(1-\sigma)^{2}(v^{k}-v^{k-1})^{2}{{\int}_{0}^{1}}(1-s)f^{(4)}\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right)\left( \nabla(v^{k-1}+s(v^{k-\sigma}-v^{k-1}))\right)^{2} \mathrm{d} s\\ &&\quad+(1-\sigma)^{2}(v^{k}-v^{k-1})^{2}{{\int}_{0}^{1}}(1-s)f^{\prime\prime\prime}\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right){\Delta}\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right) \mathrm{d} s\\ &&\quad+2(1-\sigma)^{2}\left( \nabla(v^{k}-v^{k-1})\right)^{2}{{\int}_{0}^{1}}(1-s)f^{\prime\prime}\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right) \mathrm{d} s \end{array} $$

$$ \begin{array}{@{}rcl@{}} &&\quad+2(1-\sigma)^{2}(v^{k}-v^{k-1}){\Delta}(v^{k}-v^{k-1}){{\int}_{0}^{1}}(1-s)f^{\prime\prime}\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right) \mathrm{d} s\\ &&\quad+2(1-\sigma)^{2}(v^{k}-v^{k-1})\nabla(v^{k}-v^{k-1}){{\int}_{0}^{1}}(1-s)f^{\prime\prime\prime}\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right)\\ &&\quad\quad\nabla\left( v^{k-1}+s(v^{k-\sigma}-v^{k-1})\right) \mathrm{d} s. \end{array} $$

By the condition (1.5) of v, we have

$$ \begin{array}{@{}rcl@{}} \left|R_{f}^{k-\sigma}\right|&\leq& C_{v}\left( {\int}_{t_{k-1}}^{t_{k}}\left|v^{\prime}(t)\right|dt\right)^{2}\leq C_{v}\left( {\int}_{t_{k-1}}^{t_{k}}(1+t^{\alpha-1})dt\right)^{2}\leq\begin{cases} C_{v}({\tau_{1}^{2}}+\frac{\tau_{1}^{2\alpha}}{\alpha^{2}}),& \ k=1,\\ C_{v}({\tau_{k}^{2}}+{\tau_{k}^{2}}t_{k-1}^{2(\alpha-1)}),& \ 2\leq k\leq n, \end{cases} \end{array} $$

$$ \begin{array}{@{}rcl@{}} \left|\nabla R_{f}^{k-\sigma}\right|&\leq& C_{v}\left( {\int}_{t_{k-1}}^{t_{k}}|v^{\prime}(t)|dt\right)^{2}+C_{v}{\int}_{t_{k-1}}^{t_{k}}|v^{\prime}(t)|dt{\int}_{t_{k-1}}^{t_{k}}|\nabla v^{\prime}(t)|dt\leq \begin{cases} C_{v}({\tau_{1}^{2}}+\frac{\tau_{1}^{2\alpha}}{\alpha^{2}}),& \ k=1,\\ C_{v}({\tau_{k}^{2}}+{\tau_{k}^{2}}t_{k-1}^{2(\alpha-1)}),& \ 2\leq k\leq n, \end{cases} \end{array} $$

$$ \begin{array}{@{}rcl@{}} \left|{\Delta} R_{f}^{k-\sigma}\right|&\leq& C_{v}{\int}_{t_{k-1}}^{t_{k}}|v^{\prime}(t)|dt{\int}_{t_{k-1}}^{t_{k}}|\nabla v^{\prime}(t)|dt+C_{v}\left( {\int}_{t_{k-1}}^{t_{k}}|v^{\prime}(t)|dt\right)^{2}+C_{v}\left( {\int}_{t_{k-1}}^{t_{k}}|v^{\prime}(t)|dt\right)^{2}\\ &&\quad+C_{v}\left( {\int}_{t_{k-1}}^{t_{k}}|\nabla v^{\prime}(t)|dt\right)^{2}+C_{v}{\int}_{t_{k-1}}^{t_{k}}|v^{\prime}(t)|dt{\int}_{t_{k-1}}^{t_{k}}|{\Delta} v^{\prime}(t)|dt+C_{v}{\int}_{t_{k-1}}^{t_{k}}|v^{\prime}(t)|dt{\int}_{t_{k-1}}^{t_{k}}|\nabla v^{\prime}(t)|dt\\ &\leq&\begin{cases} C_{v}({\tau_{1}^{2}}+\frac{\tau_{1}^{2\alpha}}{\alpha^{2}}),& \ k=1,\\ C_{v}({\tau_{k}^{2}}+{\tau_{k}^{2}}t_{k-1}^{2(\alpha-1)}),& \ 2\leq k\leq n. \end{cases} \end{array} $$

It can be further obtained that

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{k=1}^{n}P_{n-k}^{(n)}\left|R_{f}^{k-\sigma}\right|+{\sum}_{k=1}^{n}P_{n-k}^{(n)}\left|\nabla R_{f}^{k-\sigma}\right|+\sum\limits_{k=1}^{n}P_{n-k}^{(n)}\left|{\Delta} R_{f}^{k-\sigma}\right|\\ &\leq& P_{n-1}^{(n)}\left|R_{v}^{1-\sigma}\right|+\max_{2\leq k\leq n}\left|R_{f}^{k-\sigma}\right|\sum\limits_{k=2}^{n}P_{n-k}^{(n)}+P_{n-1}^{(n)}\left|\nabla R_{v}^{1-\sigma}\right|+\max_{2\leq k\leq n}\left|\nabla R_{f}^{k-\sigma}\right|{\sum}_{k=2}^{n}P_{n-k}^{(n)}\\ &&\quad+P_{n-1}^{(n)}\left|{\Delta} R_{v}^{1-\sigma}\right|+\max_{2\leq k\leq n}\left|{\Delta} R_{f}^{k-\sigma}\right|{\sum}_{k=2}^{n}P_{n-k}^{(n)}\\ &\leq& C_{v}\left[\tau_{1}^{3\alpha}+\max_{2\leq k\leq n}t_{n}^{\alpha}\left( {\tau_{k}^{2}}+{\tau_{k}^{2}}t_{k-1}^{2\alpha-2}\right)\right], \end{array} $$

where C_v in different places represents different constant. The proof is completed. □