Detection and correction of silent errors in the conjugate gradient algorithm

Abstract

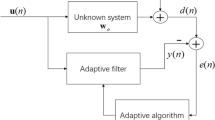
We propose a new way to detect and correct silent errors in the conjugate gradient algorithm. The detection criterion is simple, cheap to implement, and can be used at each iteration. This simplifies the correction process. Numerical experiments show that the new criterion is robust and reliable.

Appendix A: CG local orthogonality

Using (2) it can be shown that

$$\begin{aligned} \vert (r_{k}, r_{k-1})\vert\le & {} \kappa (A)\, \frac{\Vert r_{k-1}\Vert }{\Vert p_{k-1}\Vert } \left[ C_{k-1}^A u \frac{\Vert r_{k-1}\Vert }{\Vert p_{k-1}\Vert }\,\frac{\Vert r_{k-1}\Vert ^2}{\Vert r_{k-2}\Vert ^2} + \Vert r_{k-1}\Vert \,\Vert \delta _{k-2}^p\Vert \right] \nonumber \\&+ \Vert \delta _{k-1}^r\Vert \,\Vert r_{k-1}\Vert , \end{aligned}$$

(A1)

where $\kappa (A)$ is the condition umber of A and $C_{k-1}^A$ is a constant involved in the bound $\vert (Ap_{k-2}, p_{k-1})\vert \le \lambda _n C_{k-1}^A u$ where $\lambda _n$ is the largest eigenvalue of A.

The three terms in the right-hand side of inequality (A1) are small provided that the ratios are bounded and $\kappa (A)$ is not too large. Local orthogonality is, in general, well satisfied.