Skip to main content
Springer Nature Link
Log in

An hp-version fractional collocation method for Volterra integro-differential equations with weakly singular kernels

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

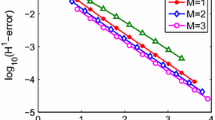
In this paper, we propose an \(\varvec{hp}\)-version fractional collocation method for solving second kind Volterra integro-differential equations with weakly singular kernels. We derive \(\varvec{hp}\)-version error estimates in a weighted \(\varvec{H}^{1}\)-norm for the method on arbitrary meshes. The results show that for any given mesh partition, exponential rates of convergence can be achieved for certain weakly singular solutions by linearly increasing the degrees of piecewise fractional polynomials. The results also imply that in the case of uniform mesh, the method has no (\(\varvec{h}\)-version) order barrier for weakly singular solutions, which is different from classical polynomial collocation methods. The method is easy to implement and has the same computational complexity as polynomial collocation methods. Numerical experiments are presented to demonstrate the efficiency of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data availability

All data generated or analyzed during this study are included in this published article.

References

  1. Brunner, H.: Nonpolynomial spline collocation for Volterra equations with weakly singular kernels. SIAM J. Numer. Anal. 20(6), 1106–1119 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  2. Brunner, H.: Polynomial spline collocation methods for Volterra integrodifferential equations with weakly singular kernels. IMA J. Numer. Anal. 6(2), 221–239 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  3. Brunner, H.: Collocation Methods for Volterra Integral and Related Functional Differential Equations. Cambridge Monographs on Applied and Computational Mathematics, vol. 15, p. 597. Cambridge University Press (2004)

  4. Lubich, C.: On the stability of linear multistep methods for Volterra convolution equations. IMA J. Numer. Anal. 3(4), 439–465 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  5. Tang, T.: Superconvergence of numerical solutions to weakly singular Volterra integro-differential equations. Numer. Math. 61(3), 373–382 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  6. Tang, T.: A note on collocation methods for Volterra integro-differential equations with weakly singular kernels. IMA J. Numer. Anal. 13(1), 93–99 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  7. Hu, Q.: Stieltjes derivatives and β-polynomial spline collocation for Volterra integrodifferential equations with singularities. SIAM J. Numer. Anal. 33(1), 208–220 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  8. Lubich, C.: Runge-Kutta theory for Volterra and Abel integral equations of the second kind. Math. Comp. 41(163), 87–102 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  9. Brunner, H., Pedas, A., Vainikko, G.: Piecewise polynomial collocation methods for linear Volterra integro-differential equations with weakly singular kernels. SIAM J. Numer. Anal. 39(3), 957–982 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  10. Hu, Q.: Geometric meshes and their application to Volterra integro-differential equations with singularities. IMA J. Numer. Anal. 18(1), 151–164 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  11. Mustapha, K.: A superconvergent discontinuous Galerkin method for Volterra integro-differential equations, smooth and non-smooth kernels. Math. Comp. 82(284), 1987–2005 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  12. Zhou, Y., Stynes, M.: Block boundary value methods for linear weakly singular Volterra integro-differential equations. BIT 61(2), 691–720 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  13. Wei, Y., Chen, Y.: Convergence analysis of the spectral methods for weakly singular Volterra integro-differential equations with smooth solutions. Adv. Appl. Math. Mech. 4(1), 1–20 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  14. Shi, X., Chen, Y.: Spectral-collocation method for Volterra delay integro-differential equations with weakly singular kernels. Adv. Appl. Math. Mech. 8(4), 648–669 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  15. Yang, Y., Chen, Y.: Spectral collocation methods for nonlinear Volterra integro-differential equations with weakly singular kernels. Bull. Malays. Math. Sci. Soc. 42(1), 297–314 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  16. Gu, Z.: Spectral collocation method for weakly singular Volterra integro-differential equations. Appl. Numer. Math. 143, 263–275 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  17. Baratella, P., Palamara Orsi, A.: Numerical solution of weakly singular linear Volterra integro-differential equations. Computing 77(1), 77–96 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  18. Diogo, T., Lima, P.M., Pedas, A., Vainikko, G.: Smoothing transformation and spline collocation for weakly singular Volterra integro-differential equations. Appl. Numer. Math. 114, 63–76 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  19. Shi, X., Wei, Y., Huang, F.: Spectral collocation methods for nonlinear weakly singular Volterra integro-differential equations. Numer. Methods Partial Differential Equations 35(2), 576–596 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  20. Hou, D., Xu, C.: A fractional spectral method with applications to some singular problems. Adv. Comput. Math. 43(5), 911–944 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  21. Brunner, H., Schötzau, D.: hp-discontinuous Galerkin time-stepping for Volterra integrodifferential equations. SIAM J. Numer. Anal. 44(1), 224–245 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  22. Yi, L., Guo, B.: An h-p version of the continuous Petrov-Galerkin finite element method for Volterra integro-differential equations with smooth and nonsmooth kernels. SIAM J. Numer. Anal. 53(6), 2677–2704 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  23. Yi, L.: An h-p version of the continuous Petrov-Galerkin finite element method for nonlinear Volterra integro-differential equations. J. Sci. Comput. 65(2), 715–734 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  24. Wang, Z., Guo, Y., Yi, L.: An hp-version Legendre-Jacobi spectral collocation method for Volterra integro-differential equations with smooth and weakly singular kernels. Math. Comp. 86(307), 2285–2324 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  25. Wang, C., Wang, Z., Jia, H.: An hp-version spectral collocation method for nonlinear Volterra integro-differential equation with weakly singular kernels. J. Sci. Comput. 72(2), 647–678 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  26. Jia, H., Yang, Y., Wang, Z.: An hp-version Chebyshev spectral collocation method for nonlinear Volterra integro-differential equations with weakly singular kernels. Numer. Math. Theory Methods Appl. 12(3), 969–994 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  27. Shen J., Tang T., Wang L.: Spectral Methods: Algorithms, Analysis and Applications vol. 41. Springer (2011)

  28. Sheng, C., Wang, Z., Guo, B.: A multistep Legendre-Gauss spectral collocation method for nonlinear Volterra integral equations. SIAM J. Numer. Anal. 52(4), 1953–1980 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  29. Guo, B., Wang, Z.: Legendre-Gauss collocation methods for ordinary differential equations. Adv. Comput. Math. 30(3), 249–280 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  30. Hou, D., Lin, Y., Azaiez, M., Xu, C.: A Müntz-collocation spectral method for weakly singular Volterra integral equations. J. Sci. Comput. 81(3), 2162–2187 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  31. Ma, Z., Alikhanov, A.A., Huang, C., Zhang, G.: A multi-domain spectral collocation method for Volterra integral equations with a weakly singular kernel. Appl. Numer. Math. 167, 218–236 (2021)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to the anonymous referees and the editors for their valuable suggestions and comments.

Funding

This work was supported by the National Natural Science Foundation of China (Nos. 12171177 and 12011530058).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan, 430074, China

    Zheng Ma & Chengming Huang

  2. Hubei Key Laboratory of Engineering Modeling and Scientific Computing, Huazhong University of Science and Technology, Wuhan, 430074, China

    Chengming Huang

Authors
  1. Zheng Ma
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Chengming Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Chengming Huang.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ma, Z., Huang, C. An hp-version fractional collocation method for Volterra integro-differential equations with weakly singular kernels. Numer Algor 92, 2377–2404 (2023). https://doi.org/10.1007/s11075-022-01394-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-022-01394-9

Keywords