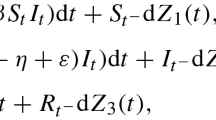Skip to main content
SpringerLink
Log in

Numerical analysis of a linearly backward Euler method with truncated Wiener process for a stochastic SIS model

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

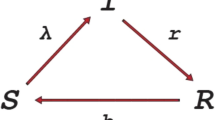
The paper deals with the numerical positivity, convergence and dynamical behaviors (including extinction and persistence) for stochastic SIS model. Compared with the existing numerical methods, a linearly backward Euler method with truncated Wiener process is introduced with a less computational cost and a better dynamic behavior. We discuss the numerical positivity by the truncated Wiener process, which is the basis for the investigation of convergence and dynamic behavior. The numerical dynamical behaviors (extinction and persistence) are obtained by an exponential representation for the nonlinear stochastic stability function and the large number theorem for martingale, which reproduces the existing theoretical results of exact solution. Finally, numerical examples are given to validate our numerical results for stochastic SIS model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data Availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. Calvo, M.P., de Frutos, J., Novo, J.: Linearly implicit runge-Kutta methods for advection-reaction-diffusion equations. Appl. Numer. Math. 37(4), 535–549 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  2. Du, N.H., Nhu, N.N.: Permanence and extinction for the stochastic SIR epidemic model. J. Differential. Equations. 269(11), 9619–9652 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  3. Gray, A., Greenhalgh, D., Hu, L., Mao, X., Pan, J.: A stochastic differential equation SIS epidemic model. SIAM J. Appl. Math. 71(3), 876–902 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  4. Guo, P., Li, C.: Almost sure exponential stability of numerical solutions for stochastic pantograph differential equations. J. Math. Anal. Appl. 460 (1), 411–424 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  5. Higham, D.J., Mao, X.R., Yuan, C.G.: Almost sure and moment exponential stability in the numerical simulation of stochastic differential equations. SIAM J. Numer. Anal. 45(2), 592–609 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  6. Iannelli, M., Milner, F.A., Pugliese, A.: Analytical and numerical results for the age-structured s-I-S epidemic model with mixed inter-intracohort transmission. SIAM J. Math. Anal. 23(3), 662–688 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  7. Kahl, C., Günther, M., Rossberg, T.: Structure preserving stochastic integration schemes in interest rate derivative modeling. Appl. Numer. Math. 58(3), 284–295 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  8. Khasminskii, R.: Stochastic Stability of Differential Equations, Stochastic Modelling and Applied Probability, 2nd edn., vol. 66. Springer, Heidelberg (2012). with contributions by G. N. Milstein and M. B. Nevelson

  9. Li, X., Zhang, C., Ma, Q., Ding, X.: Arbitrary high-order EQUIP methods for stochastic canonical Hamiltonian systems. Taiwanese. J. Math. 23 (3), 703–725 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  10. Mao, X.R.: Stochastic Differential Equations and Applications, 2nd edn. Horwood Publishing Limited, Chichester (2008)

    Book  Google Scholar 

  11. Milstein, G.N., Platen, E., Schurz, H.: Balanced implicit methods for stiff stochastic systems. SIAM J. Numer. Anal. 35(3), 1010–1019 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  12. Milstein, G.N., Repin, Y.M., Tretyakov, M.V.: Numerical methods for stochastic systems preserving symplectic structure. SIAM J. Numer. Anal. 40(4), 1583–1604 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  13. Wu, F.K., Mao, X.R., Szpruch, L.: Almost sure exponential stability of numerical solutions for stochastic delay differential equations. Numer. Math. 115(4), 681–697 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  14. Yang, H.Z., Yang, Z.W., Ma, S.F.: Theoretical and numerical analysis for Volterra integro-differential equations with itô integral under polynomially growth conditions. Appl. Math. Comput. 360, 70–82 (2019)

    MathSciNet  MATH  Google Scholar 

  15. Yang, Z.W., Zhang, J.W., Zhao, C.C.: Numerical blow-up analysis of linearly implicit Euler method for nonlinear parabolic integro-differential equations. J. Comput. Appl. Math. 358, 343–358 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  16. Zhang, R., Wang, J.L., Liu, S.Q.: Traveling wave solutions for a class of discrete diffusive SIR epidemic model. J. Nonlinear. Sci. 31(1), Paper No. 10, 33 (2021)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to express their gratitude to the reviewers: their valuable comments and suggestions led to a greatly improved version of the paper.

Funding

This research was supported by the National Natural Science Foundation of China (NSFC 11871179 and NSFC 11771128).

Author information

Authors and Affiliations

  1. School of Mathematics, Harbin Institute of Technology, Harbin, China

    Xiaochen Yang, Mengna Li, Zhanwen Yang & Chiping Zhang

Authors
  1. Xiaochen Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mengna Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhanwen Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Chiping Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhanwen Yang.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, X., Li, M., Yang, Z. et al. Numerical analysis of a linearly backward Euler method with truncated Wiener process for a stochastic SIS model. Numer Algor 93, 563–579 (2023). https://doi.org/10.1007/s11075-022-01427-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-022-01427-3

Keywords

Mathematics Subject Classification (2010)

Search

Navigation