Abstract
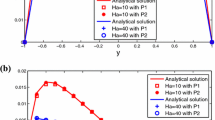
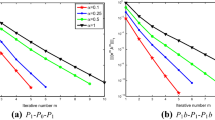
In this article, we mainly consider a first-order decoupling penalty method for the 2D/3D time-dependent incompressible magnetohydrodynamic (MHD) equations in a convex domain. This method applies a penalty term to the constraint “divu = 0,” which allows us to transform the saddle point problem into two small problems to solve. The time discretization is based on the backward Euler scheme. Moreover, we derive the optimal error estimate for the penalty method under semi-discretization with the relationship 𝜖 = O(Δt). Finally, we give abundant of numerical tests to verify the theoretical result and the spatial discretization is based on Lagrange finite element.











Similar content being viewed by others
Data availability
All data generated or analyzed during this study are included in this published article.
References
Baty, H., Keppens, R., Comte, P.: The two-dimensional magnetohydrodynamic Kelvin-Helmholtz instability: compressibility and large-scale coalescence effects. Phys. Plasmas 10(12), 4661–4674 (2003)
Becker, R., Hansbo, P.: A simple pressure stabilization method for the Stokes equation. Commun. Numer. Methods Eng. 24(11), 1421–1430 (2008)
Brezzi, F., Pitkäranta, J.: On the stabilization of finite element approximations of the Stokes equations. Springer, Wiesbaden (1984)
Chorin, A.: Numerical solution of the Navier-Stokes equations. Math. Comput. 22(104), 745–762 (1968)
Chorin, A.: On the convergence of discrete approximations to the Navier-Stokes equations. Math. Comput. 23(106), 341–353 (1969)
Courant, R.: Variational methods for the solution of problems of equilibrium and vibrations. Bull. Am. Math. Soc. 49, 1–23 (1943)
Deng, J., Si, Z.: A decoupling penalty finite element method for the stationary incompressible magnetohydrodynamics equation. Int. J. Heat Mass Transf. 128, 601–612 (2019)
Donatelli, D.: The artificial compressibility approximation for MHD equations in unbounded domain. J. Hyperbolic Differ. Equ. 10(1), 181–198 (2013)
Dong, X., He, Y., Zhang, Y.: Convergence analysis of three finite element iterative methods for the 2D/3D stationary incompressible magnetohydrodynamics. Comput. Methods Appl. Mech. Eng. 276, 287–311 (2014)
Girault, V., Raviart, P.: Finite element methods for Navier-Stokes equations: theory and algorithms. Springer, Berlin (1987)
Goedbloed, J., Keppens, R., Poedts, S.: Advanced magnetohydrodynamics: with applications to laboratory and astrophysical plasmas. Cambridge University Press, Cambridge (2010)
Gunzburger, M., Meir, A., Peterson, J.: On the existence, uniqueness, and finite element approximation of solutions of the equations of stationary, incompressible magnetohydrodynamics. Math. Comput. 56(194), 523–563 (1991)
He, Y.: Optimal error estimate of the penalty finite element method for the time-dependent Navier-Stokes equations. Math. Comput. 74(251), 1201–1216 (2005)
He, Y.: Unconditional convergence of the Euler semi-implicit scheme for the three-dimensional incompressible MHD equations. IMA J. Numer. Anal. 35(2), 767–801 (2015)
He, Y., Li, J.: A penalty finite element method based on the Euler implicit/explicit scheme for the time-dependent Navier-Stokes equations. J. Comput. Appl. Math. 235(3), 708–725 (2010)
Heywood, J., Rannacher, R.: Finite element approximation of the nonstationary Navier-Stokes problem. I. Regularity of solutions and second order error estimates for spatial discretization. SIAM J. Numer. Anal. 19(2), 275–311 (1982)
John, V.: Reference values for drag and lift of a two-dimensional time-dependent flow around a cylinder. Int. J. Numer. Methods Fluids 44(7), 777–788 (2004)
Lu, X., Lin, P.: Error estimate of the P1 nonconforming finite element method for the penalized unsteady Navier-Stokes equations. Numer. Math. 115(2), 261–287 (2010)
Priest, E., Hood, A.: Advances in solar system magnetohydrodynamics. Cambridge University Press, Cambridge (1991)
Sermange, M., Temam, R.: Some mathematical questions related to the MHD equations. Commun. Pure Appl. Math. 36(4), 635–664 (1983)
Shen, J.: On error estimates of the penalty method for unsteady Navier-Stokes equations. SIAM J. Numer. Anal. 32(2), 386–403 (1995)
Su, H., Feng, X., Huang, P.: Iterative methods in penalty finite element discretization for the steady MHD equations. Comput. Methods Appl. Mech. Eng. 304, 521–545 (2016)
Su, H., Feng, X., Zhao, J.: On two-level Oseen penalty iteration methods for the 2D/3D stationary incompressible magnetohydronamics. J. Sci. Comput. 83(1), 1–30 (2020)
Su, H., Mao, S., Feng, X.: Optimal error estimates of penalty based iterative methods for steady incompressible magnetohydrodynamics equations with different viscosities. J. Sci. Comput. 79(2), 1078–1110 (2019)
Témam, R.: Sur l’approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (I). Arch. Ration. Mech. Anal. 32(2), 135–153 (1969)
Témam, R.: Sur l’approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (II). Arch. Ration. Mech. Anal. 33(5), 377–385 (1969)
Yang, J., He, Y.: Stability and error analysis for the first-order Euler implicit/explicit scheme for the 3D MHD equations. Int. J. Comput. Methods 14(2), 1750077 (2017)
Yang, J., He, Y., Zhang, G.: On an efficient second order backward difference Newton scheme for MHD system. J. Math. Anal. Appl. 458(1), 676–714 (2018)
Yang, X., Zhang, G., He, X.: Convergence analysis of an unconditionally energy stable projection scheme for magneto-hydrodynamic equations. Appl. Numer. Math. 136(1), 235–256 (2019)
Yang, Y., Si, Z.: A consistent projection finite element method for the incompressible MHD equations. Appl. Anal. 100(12), 2606–2626 (2021)
Zhang, G., Chen, C.: Uniformly robust preconditioners for incompressible MHD system. J. Comput. Appl. Math. 379, 112914 (2020)
Zhang, G., He, X., Yang, X.: A decoupled, linear and unconditionally energy stable scheme with finite element discretizations for magneto-hydrodynamic equations. J. Sci. Comput. 81(3), 1678–1711 (2019)
Zhang, G., He, X., Yang, X.: Fully decoupled, linear and unconditionally energy stable time discretization scheme for solving the magneto-hydrodynamic equations. J. Comput. Appl. Math. 369, 112636 (2020)
Zhang, G., He, Y.: Decoupled schemes for unsteady MHD equations. I. Time discretization. Numer. Methods for Partial Differ. Equ. 33(3), 956–973 (2017)
Zhang, Q., Su, H., Feng, X.: A partitioned finite element scheme based on gauge-Uzawa method for time-dependent MHD equations. Numer. Algoritm. 78(1), 277–295 (2017)
Acknowledgements
The authors are very much indebted to the referees for their constructive suggestions and insightful comments, which greatly improved the original manuscript of this paper.
Funding
This work is partly supported by the NSF of China (No. 12126361, 12126372, 12061076), Tianshan Youth Project of Xinjiang Province (No. 2017Q079), Scientific Research Plan of Universities in the Autonomous Region (No. XJEDU2020I 001), and Key Laboratory Open Project of Xinjiang Province (No. 2020D04002).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Shi, K., Feng, X. & Su, H. Optimal error estimate of the penalty method for the 2D/3D time-dependent MHD equations. Numer Algor 93, 1337–1371 (2023). https://doi.org/10.1007/s11075-022-01470-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-022-01470-0