Skip to main content
Springer Nature Link
Log in

A real unconstrained equivalent problem of the quaternion equality constrained weighted least squares problem

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

In this paper, we focus on the quaternion equality constrained weighted least squares problem. First, according to the properties of the Moore-Penrose generalized inverse matrix, the singular value decomposition, the CS decomposition, and the real representation matrices of quaternion matrices, we obtain a real unconstrained equivalent problem of the quaternion equality constrained weighted least squares problem. And then we give the expressions of its general solution and minimal norm solution. Finally, according to the properties of the real representation matrices of quaternion matrices, the special structure of real representation matrices and the real structure-preserving singular value decomposition of quaternion matrix, we propose a real structure-preserving algorithm for the minimal norm solution of the quaternion equality constrained weighted least squares problem, and illustrate the effectiveness of proposed algorithm by a numerical example.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Algorithm 1
Fig. 1
Fig. 2

Similar content being viewed by others

Data Availability

The datasets generated during the current study are available from the corresponding author on reasonable request.

References

  1. Eldén, L.: Perturbation theory for the least squares problem with linear equality constraints. SIAM. J. Numer. Anal. 17, 338–350 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  2. Wei, M.: Perturbation theory for the rank-deficient equality constrained least squares problem. SIAM. J. Numer. Anal. 29, 1462–1481 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  3. Ding, J.: On the perturbation of least squares problems with equality constraints. Linear Multilinear A. 45, 35–47 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  4. De Pierro, A. R., Wei, M.: Some new properties of the equality constrained and weighted least squares problem. Linear Algebra Appl. 320, 145–165 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  5. Liu, Q.: Stability of the MGS-like elimination method for equality constrained least squares problems. J. Shanghai Univ. 13, 213–218 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  6. Liu, Q., Wei, M.: On direct elimination methods for solving the equality constrained least squares problem. Linear Multilinear A. 58, 173–184 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  7. Li, H., Wang, S.: Partial condition number for the equality constrained linear least squares problem. Calcolo 54, 1121–1146 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  8. Zeb, S., Yousaf, M.: Repeated QR updating algorithm for solution of equality constrained linear least squares problems. J. Inequal. Appl. 1, 281 (2017)

    Article  MATH  Google Scholar 

  9. Diao, H.: Condition numbers for a linear function of the solution of the linear least squares problem with equality constraints. J. Comput. Appl. Math. 344, 640–656 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  10. Adler, S. L.: Scattering and decay theory for quaternionic quantum mechanics and the structure of induced T non-conservation. Phys. Rev. D. 37, 3654–3662 (1988)

    Article  MathSciNet  Google Scholar 

  11. Faßbender, H., Mackey, D. S., Mackey, N.: Hamilton and Jacobi come full circle: Jacobi algorithms for structured Hamiltonian problems. Linear Algebra Appl. 332, 37–80 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  12. Finkelstein, D., Jauch, J. M., Schiminovich, S., Speiser, D.: Principle of general Q-covariance. J. Math. Phys. 4, 788–796 (1963)

    Article  MathSciNet  MATH  Google Scholar 

  13. Ji, P., Wu, H.: A closed-form forward kinematics solution for the 6-6p Stewart platform. IEEE Trans. Robot. Autom. 17, 522–526 (2001)

    Article  Google Scholar 

  14. Liu, X., Wu, Y., Zhang, H., Wu, J., Zhang, L.: Quaternion discrete fractional Krawtchouk transform and its application in color image encryption and watermarking. Signal Process. 189, 108275 (2021)

    Article  Google Scholar 

  15. De Leo, S.: Quaternion and special relativity. J. Math. Phys. 37, 2955–2968 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  16. Finkelstein, D., Jauch, J. M., Speiser, D.: Quaternionic representations of compact groups. J. Math. Phys. 4, 136–140 (1963)

    Article  MathSciNet  MATH  Google Scholar 

  17. Jiang, T., Zhao, J., Wei, M.: A new technique of quaternion equality constrained least squares problem. J. Comput. Appl. Math. 216, 509–513 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  18. Li, Y., Zhang, Y., Wei, M., Zhao, H.: Real structure-preserving algorithm for quaternion equality constrained least squares problem. Math. Method Appl. Sci. 43, 4558–4566 (2019)

    MathSciNet  MATH  Google Scholar 

  19. Zhang, Y., Li, Y., Wei, M., Zhao, H.: An algorithm based on QSVD for the quaternion equality constrained least squares problem. Numer. Algor. 4, 1–14 (2020)

    Google Scholar 

  20. Zhang, F., Zhao, J.: A real structure-preserving algorithm based on the quaternion QR decomposition for the quaternion equality constrained least squares problem. Numer. Algor. 91, 1815–1827 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  21. Jia, Z., Wei, M., Ling, S.: A new structure-preserving menthod for quaternion Hermitian eigenvalue problems. J. Comput. Appl. Math. 239, 12–24 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  22. Li, Y., Wei, M., Zhang, F., Zhao, J.: A fast structure-preserving method for computing the singular value decomposition of quaternion matrices. Appl. Math. Comput. 235, 157–167 (2014)

    MathSciNet  MATH  Google Scholar 

  23. Li, Y., Wei, M., Zhang, F., Zhao, J.: A real structure-preserving method for the quaternion LU decomposition, revisited. Calcolo 54, 1553–1563 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  24. Li, Y., Wei, M., Zhang, F., Zhao, J.: Real structure-preserving algorithms of Householder based transformations for quaternion matrices. J. Comput. Appl. Math. 305, 82–91 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  25. Jia, Z., Wei, M., Zhao, M., Chen, Y.: A new real structure-preserving quaternion QR algorithm. J. Comput. Appl. Math. 343, 26–48 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  26. Zhang, F., Wei, M., Li, Y., Zhao, J.: Special least squares solutions of the quaternion matrix equation AX = b with applications. Appl. Math. Comput. 270, 425–433 (2015)

    MathSciNet  MATH  Google Scholar 

  27. Zhang, F., Mu, W., Li, Y., Zhao, J.: Special least squares solutions of the quaternion matrix equation AXB + CXD = e. Comput. Math. Appl. 72, 1426–1435 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  28. Wei, M., Li, Y., Zhang, F., Zhao, J.: Quaternion matrix computations. Nova Science Publisher, New York (2018)

    Google Scholar 

  29. Li, Y., Wei, M., Zhang, F., Zhao, J.: Comparison of two SVD-based color image compression schemes, vol. 12 (2017)

  30. Jia, Z.: The eigenvalue problem of quaternion matrix: structure-preserving algorithms and applications. Science Publisher, Beijing (2019)

    Google Scholar 

  31. Jia, Z., Jin, Q., Ng, M. K., Zhao, X.: Non-local robust quaternion matrix completion for large-scale color image and video inpainting. IEEE Trans. Image Process. 31, 3868–3883 (2022)

    Article  Google Scholar 

  32. Liu, Q., Ling, S., Jia, Z.: Randomized quaternion singular value decomposition for low-rank matrix approximation. SIAM. J. Sci. Comput. 44(2), A870–A900 (2022)

    MATH  Google Scholar 

  33. Jia, Z., Ng, M. K.: Structure preserving quaternion generalized minimal residual method. SIAM. J. Matrix Anal. A. 42(2), 616–634 (2021)

    Article  MATH  Google Scholar 

  34. Jia, Z., Ng, M. K., Wang, W.: Color image restoration by saturation-value total variation. SIAM. J. Imaging Sci. 12(2), 972–1000 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  35. Jia, Z., Ng, M. K., Song, G.: Robust quaternion matrix completion with applications to image inpainting. Numer. Linear Algebra 26(4), e2245 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  36. Sangwine, S. J., Le Bihan, N.: Quaternion toolbox for MATLAB. http://qtfm.sourceforge.net/

Download references

Funding

This paper is supported by the Natural Science Foundation of Shandong Province of China (Nos. ZR2022MA030 and ZR2020MA053), the Scientific Research Foundation of Liaocheng University (No. 318011921), and Discipline with Strong Characteristics of Liaocheng University - Intelligent Science and Technology (No. 319462208).

Author information

Authors and Affiliations

  1. College of Mathematical Science, Liaocheng University, Liaocheng, 252000, People’s Republic of China

    Fengxia Zhang, Ying Li & Jianli Zhao

Authors
  1. Fengxia Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ying Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jianli Zhao
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

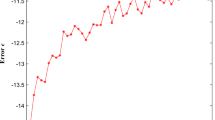
Fengxia Zhang wrote the main manuscript text and Ying Li prepared Figures 1–2. All authors reviewed the manuscript.

Corresponding author

Correspondence to Fengxia Zhang.

Ethics declarations

Consent for publication

All authors agree to publish this paper and related contents.

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, F., Li, Y. & Zhao, J. A real unconstrained equivalent problem of the quaternion equality constrained weighted least squares problem. Numer Algor 94, 73–91 (2023). https://doi.org/10.1007/s11075-022-01493-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-022-01493-7

Keywords