Numerical solution to the exterior Bernoulli problem using the Dirichlet-Robin energy gap cost functional approach in two and three dimensions

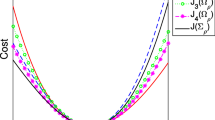
Abstract

The exterior Bernoulli problem — a prototype stationary free boundary problem — is rephrased into a shape optimization setting using an energy-gap type cost functional that is subject to two auxiliary problems: a pure Dirichlet problem and a mixed Dirichlet-Robin boundary value problem. It is demonstrated here that depending on what method is used, the shape gradient of the cost functional may appear in a different form. The dissimilarity in structure comes from the way the adjoint variable was utilized in the computation — then resulting to a different adjoint problem. The shape derivative is first obtained via Delfour-Zolésio’s minimax formulation, and then by using the weak form of the Eulerian derivative of the states coupled with the adjoint method. The latter approach is accomplished by first showing the existence of the derivatives. A fast iterative scheme based on finite element method is then formulated to numerically solve the proposed shape optimization formulation. The feasibility of the method — highlighting its efficiency and practicality — is illustrated through numerical examples in two and three dimensions.

Appendix. Correa-Seeger theorem

Let ε > 0 be a fixed real number and consider a functional

$$ G:[0,{\varepsilon}]\times X \times Y \to \mathbb{R}, $$

for some topological spaces X and Y. For each t ∈ [0,ε], we define

$$ M(t) := \min_{x\in X} \sup_{y\in Y} G(t,x,y) \quad\text{and}\quad m(t) = \sup_{y\in Y} \min_{x\in X} G(t,x,y), $$

and the associated sets

$$ \begin{array}{@{}rcl@{}} X(t) &:= \left\{ \hat{x} \in X : \sup\limits_{y\in Y} G(t,\hat{x}, y) = M(t)\right\}\\ Y(t) &:= \left\{ \hat{y} \in Y : \min\limits_{x\in X} G(t,x,\hat{y}) = m(t)\right\}. \end{array} $$

We introduce the set of saddle points

$$ S(t)=\{(\hat{x},\hat{y})\in X\times Y : M(t) = G(t, \hat{x}, \hat{y}) = m(t)\}, $$

which may be empty. In general, we always have the inequality $m(t) \leqslant M(t)$, and when m(t) = M(t), the set S(t) is exactly X(t) × Y (t).

We have the following theorem (see [35, Thm. 5.1, pp. 556–559]).

Theorem A.1 (Correa and Seeger, [43])

Let the sets X and Y, the real number ε > 0, and the functional $G: [0,{\varepsilon }] \times X \times Y \to \mathbb {R}$ be given. Assume that the following assumptions hold:

(H1):

for $0 \leqslant t \leqslant {\varepsilon }$, the set S(t) is non-empty;

(H2):

the partial derivative ∂_tG(t,x,y) exists everywhere in [0,ε], for all $(x,y) \in \left (\bigcup _{t \in [0,\varepsilon ]} X(t) \times Y(0) \right ) \bigcup \left (X(0) \times \bigcup _{t \in [0,\varepsilon ]} Y(t) \right )$;

(H3):

there exists a topology $\mathcal {T}_{X}$ on X such that for any sequence $\{t_{n} : 0 < t_{n} \leqslant {\varepsilon }\}, t_{n} \to t_{0} = 0$, there exist an x⁰ ∈ X(0) and a subsequence $\{t_{n_{k}} \}$ of {t_n}, and for each $k \geqslant 1$, there exists $x_{n_{k}} \in X(t_{n_{k}})$ such that (i) $x_{n_{k}} \to x^{0}$ in the $\mathcal {T}_{X}$-topology, and (ii) for all y in Y (0), $\liminf _{t\searrow 0,\ k \to \infty } \partial _{t}G(t, x_{n_{k}} , y) \geqslant \partial _{t}G(0, x^{0}, y)$;

(H4):

there exists a topology $\mathcal {T}_{Y}$ on Y such that for any sequence $\{t_{n} : 0 < t_{n} \leqslant {\varepsilon }\}, t_{n} \to t_{0} = 0$, there exist y⁰ ∈ Y (0) and a subsequence $\{t_{n_{k}} \}$ of {t_n}, and for each $k \geqslant 1$, there exists $y_{n_{k}} \in Y(t_{n_{k}})$ such that (i) $y_{n_{k}} \to y^{0}$ in the $\mathcal {T}_{Y}$-topology, and (ii) for all x in X(0), $\limsup _{t\searrow 0,\ k \to \infty } \partial _{t}G(t, x, y_{n_{k}}) \leqslant \partial _{t}G(0, x, y^{0})$;

Then, there exists (x⁰,y⁰) ∈ X(0) × Y (0) such that

$$ {d}g(0) = \min_{x\in X(0)} \sup_{y\in Y(0)} \partial_{t}G(0, x, y) = \partial_{t}G(0, x^{0}, y^{0}) = \sup_{y\in Y(0)} \min_{x\in X(0)} \partial_{t}G(0,x,y). $$

Thus, (x⁰,y⁰) is a saddle point of ∂_tG(0,x,y) on X(0) × Y (0).