Skip to main content
Springer Nature Link
Log in

A proper orthogonal decomposition-compact difference algorithm for plate vibration models

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

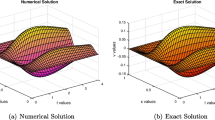
In this article, we propose a proper orthogonal decomposition-compact difference scheme (POD-CDS) for the displacement-stress form of a simply supported plate vibration model. We prove that the POD-CDS can preserve the same spatial and temporal convergence rates and unconditional stability with the control constant independent of the time levels for the displacement and the stress in discrete \(H^1\)-norm as the compact difference solution does, as well as improve the computing efficiency significantly, which confirms the reliability of the POD-CDS for long time simulation of the vibration models. Furthermore, we conduct the stability and convergence analysis for the corresponding compact difference scheme in discrete \(H^k\)-norm as \(k=0,1,2,\) respectively, which compensates those missing estimates of the references Q. Li and Q. Yang (Adv. Differ. Equ. 328: 1–19, 2019) and Q. Li, Q. Yang, and H. Chen (Numer. Methods Partial Differ. Equ. 36: 1938–1961, 2020). Numerical experiments are provided to verify these theoretical findings and show that the POD-CDS possesses nearly 10–30 times computing efficiency faster than the compact difference scheme does.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data Availability

The datasets generated during and analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. Ames, W.: Numerical methods for partial differential equations. Academic Press, New York (1977)

    MATH  Google Scholar 

  2. Abbaszadeh, M., Dehghan, M.: The proper orthogonal decomposition modal spectral element method for two-dimensional viscoelastic equation. Thin-Walled Struct. 161, 107–429 (2021)

    Article  Google Scholar 

  3. Abbaszadeh, M., Dehghan, M.: A POD-based reduced-order Crank-Nicolson/fourth-order alternating direction implicit (ADI) finite difference scheme for solving the two-dimensional distributed-order Riesz space- fractional diffusion equation. Appl. Numer. Math. 158, 271–291 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  4. Conte, S.: Numerical solution of vibration problems in two space variables. Pac. J. Math. 4, 1535–1544 (1957)

    Article  MathSciNet  MATH  Google Scholar 

  5. Cui, M.: High order compact alternating direction implicit method for the generalized sine-Gordon equation. J. Comput. Appl. Math. 235, 837–849 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  6. Ciarlet, P.: The finite element method for elliptic problems. North-Holland Publishing Company, Amsterdam (1978)

    MATH  Google Scholar 

  7. Dennis, S., Hundson, J.: Compact \(h^4\) finite-difference approximations to operators of Navier-Stokes type. J. Comput. Phys. 85, 390–416 (1989)

    Article  MathSciNet  Google Scholar 

  8. Deng, D., Zhang, C.: Application of a fourth-order compact ADI method to solve a two-dimensional linear hyperbolic equation. Int J. Comput. Math 90, 273–291 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  9. Inman, D.: Engineering vibration. Prentice Hall, Upper Saddle River (2014)

    Google Scholar 

  10. Lele, S.: Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  11. Luo, Z., Jin, S., Chen, J.: A reduced-order extrapolation central difference scheme based on POD for two-dimensional fourth-order hyperbolic equations. Appl. Math. Comput. 289, 396–408 (2016)

    MathSciNet  MATH  Google Scholar 

  12. Li, K., Huang, T., Li, L., Lanteri, S.: A reduced-order DG formulation based on POD method for the time-domain Maxwall’s equations in dispersive media. J. Comput. Appl. Math. 336, 249–266 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  13. Li, K., Huang, T., Li, L., Lanteri, S., Xu, L., Li, B.: A reduced-order discontinuous galerkin method based on POD for electromagnetic simulation. IEEE Transactions on Antennas and Propagation. 66, 242–254 (2018)

    Article  Google Scholar 

  14. Li, H., Song, Z.: A reduced-order energy-stability-preserving finite difference iterative scheme based on POD for the Allen-Cahn equation. J. Math. Analy. Appl. 491, 124–245 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  15. Luo, Z., Ren, H.: A reduced-order extrapolated finite difference iterative method for the Riemann-Liouville tempered fractional derivative equation. Appl. Numer. Math. 157, 307–314 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  16. Li, H., Song, Z., Zhang, F.: A reduced-order modified finite diference method preserving unconditional energy-stability for the Allen-Cahn equation. Numerical Methods for Partial Differential Equations. 37, 1869–1885 (2021)

    Article  MathSciNet  Google Scholar 

  17. Li, Q., Yang, Q.: Compact difference scheme for two-dimensional fourth-order hyperbolic equation. Advances in Difference Equations. 328, 1–19 (2019)

    MathSciNet  Google Scholar 

  18. Li, Q., Yang, Q., Chen, H.: Compact difference scheme for two-dimensional fourth-order nonlinear hyperbolic equation. Numerical Methods for Partial Differential Equations. 36, 1938–1961 (2020)

    Article  MathSciNet  Google Scholar 

  19. Luo, Z., Wang, R., Zhu, J.: Finite difference scheme based on proper orthogonal decomposition for the non-stationary Navier-Stokes equations. Science in China, Ser. A: Mathematics. 50, 1186–1196 (2007)

  20. Luo, Z., Chen, G.: Proper orthogonal decomposition methods for partial differential equations. Academic Press of Elsevier, San Diego (2018)

    Google Scholar 

  21. Liao, F., Zhang, L., Wang, T.: Two energy-conserving and compact finite difference schemes for two-dimensional Schrödinger-Boussinesq equations. Numerical Algorithms. 85, 1335–1363 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  22. Pao, C., Wang, Y.: Nonlinear fourth-order elliptic equations with nonlocal boundary conditions. J. Math. Anal. Appl. 372, 351–365 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  23. Qiao, H., Cheng, A.: A fast finite difference/RBF meshless approach for time fractional convection-diffusion eqaution with non-smooth solution. Eng. Anal. Bound. Elem. 125, 280–289 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  24. Rao, S.: Vibration of continuous systems. John Wiley & Sons, INC., Hoboken, New Jersey (2007)

    Google Scholar 

  25. Song, J., Rui, H.: A reduced-order finite element method based on POD for the incompressible miscible displacement problem. Comput. Math. Appli. 98, 99–117 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  26. Sun, Z.: Numerical solutions of partial differential equations. Science Press, Beijing (2012). ((in Chinese))

    Google Scholar 

  27. Wang, Y., Guo, B.: Fourth-order compact finite difference method for fourth-order nonlinear elliptic boundary value problems. J. Comput. Appl. Math. 221, 76–97 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  28. Wang, W., Ma, C.: Several forluma of matrix norm on Kronecker products. Journal of FuJian Normal University (Natural Science Edition). 31, 10–17 (2015)

    Google Scholar 

  29. Wang, Y.: Error analysis of a compact finite difference method for fourth-order nonlinear elliptic boundary value problems. Appl. Numer. Math. 120, 53–67 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  30. Xia, H., Luo, Z.: Optimized finite difference itertive scheme based on POD technique for 2D viscoelastic wave equation. Appl. Math. Mech. (English Edition) 38, 1–12 (2017)

    Article  MathSciNet  Google Scholar 

  31. Xie, S., Yi, S., Kwon, T.: Fourth-order compact difference and alternating direction implicit schemes for telegraph equation. Comput. Phys. Commun 183, 552–569 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  32. Yang, X., Ge, Y., Zhang, L.: A class of high-order compact difference schemes for solving the Burgers’ equations. Appl. Math. Comput. 358, 394–417 (2019)

    MathSciNet  MATH  Google Scholar 

  33. Yang, J., Luo, Z.: A reduced-order extrapolating space-time continuous finite element method for the 2D Sobolev equation. Numerical Methods for Partial Differential Equations. 36, 1446–1459 (2020)

    Article  MathSciNet  Google Scholar 

  34. Zhou, Y., Zhang, Y., Liang, Y., Luo, Z.: A reduced-order extrapolated model based on splitting implicit finite difference scheme and proper orthogonal decomposition for the fourth-order nonlinear Rosenau equation. Appl. Numer. Math. 162, 192–200 (2021)

Download references

Acknowledgements

The authors would like to thank the editor and referees for their valuable advices for the improvement of this article.

Funding

Q. Li and H. Chen were supported by the NSF of China under grant Nos. 12171287, 11971276, 11471196, H. Wang was supported by the ARO MURI Grant W911NF-15-1-0562, and by the National Science Foundation under Grant DMS-2012291.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Shandong Normal University, 250014, Jinan, Shandong, China

    Qing Li & Huanzhen Chen

  2. Department of Mathematics, University of South Carolina, Columbia, SC, USA

    Hong Wang

Authors
  1. Qing Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Huanzhen Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Hong Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Huanzhen Chen.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Q., Chen, H. & Wang, H. A proper orthogonal decomposition-compact difference algorithm for plate vibration models. Numer Algor 94, 1489–1518 (2023). https://doi.org/10.1007/s11075-023-01544-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-023-01544-7

Keywords