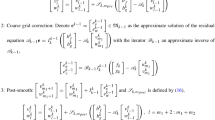Skip to main content
Springer Nature Link
Log in

Local and parallel multigrid method for semilinear Neumann problem with nonlinear boundary condition

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

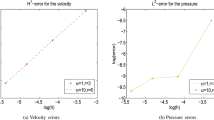
A novel local and parallel multigrid method is proposed in this study for solving the semilinear Neumann problem with nonlinear boundary condition. Instead of solving the semilinear Neumann problem directly in the fine finite element space, we transform it into a linear boundary value problem defined in each level of a multigrid sequence and a small-scale semilinear Neumann problem defined in a low-dimensional correction subspace. Furthermore, the linear boundary value problem can be efficiently solved using local and parallel methods. The proposed process derives an optimal error estimate with linear computational complexity. Additionally, compared with existing multigrid methods for semilinear Neumann problems that require bounded second order derivatives of nonlinear terms, ours only needs bounded first order derivatives. A rigorous theoretical analysis is proposed in this paper, which differs from the maturely developed theories for equations with Dirichlet boundary conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Algorithm 1
Fig. 2
Algorithm 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data Availability

All data generated or analyzed during this study are included in this published article.

References

  1. Adams, R.A.: Sobolev Spaces. Academic Press, New York (1975)

    Google Scholar 

  2. Bi, H., Li, Z., Yang, Y.: Local and parallel finite element algorithms for the Steklov eigenvalue problem. Numer. Methods Partial Differ. Equ. 32(2), 399–417 (2016)

    Article  MathSciNet  Google Scholar 

  3. Bi, H., Yang, Y., Li, H.: Local and parallel finite element discretizations for eigenvalue problems. SIAM J. Sci. Comput. 15(6), A2575–A2597 (2013)

    Article  MathSciNet  Google Scholar 

  4. Bramble, J.H., Pasciak, J.E.: New convergence estimates for multigrid algorithms. Math. Comp. 49, 311–329 (1987)

    Article  MathSciNet  Google Scholar 

  5. Bramble, J.H., Zhang, X.: The analysis of multigrid methods, Handbook of Numerical Analysis. 173–415 (2000)

  6. Brenner, S., Scott, L.: The Mathematical Theory of Finite Element Methods. Springer-Verlag, New York (1994)

    Book  Google Scholar 

  7. Chen, H., Xie, H., Xu, F.: A full multigrid method for eigenvalue problems. J. Comput. Phys. 322, 747–759 (2016)

    Article  MathSciNet  Google Scholar 

  8. Ciarlet, P.G.: The Finite Element Method for Elliptic Problems. North-Holland, Amsterdam (1978)

    Google Scholar 

  9. Dai, X., Zhou, A.: Three-scale finite element discretizations for quantum eigenvalue problems. SIAM J. Numer. Anal. 46(1), 295–324 (2008)

    Article  MathSciNet  Google Scholar 

  10. Dong, X., He, Y., Wei, H., Zhang, Y.: Local and parallel finite element algorithm based on the partition of unity method for the incompressible MHD flow. Adv. Comput. Math. 44(4), 1295–1319 (2018)

    Article  MathSciNet  Google Scholar 

  11. Du, G., Zuo, L.: Local and parallel finite element post-processing scheme for the Stokes problem. Comput. Math. Appl. 73, 129–140 (2017)

    Article  MathSciNet  Google Scholar 

  12. Du, G., Hou, Y., Zuo, L.: A modified local and parallel finite element method for the mixed Stokes-Darcy model. J. Math. Anal. Appl. 435(2), 1129–1145 (2016)

    Article  MathSciNet  Google Scholar 

  13. Grisvard, P.: Elliptic Problems in Nonsmooth Domains. Pitman, Boston, MA (1985)

    Google Scholar 

  14. He, Y., Mei, L., Shang, Y., Cui, J.: Newton iterative parallel finite element algorithm for the steady Navier-Stokes equations. J. Sci. Comput. 44, 92–106 (2010)

    Article  MathSciNet  Google Scholar 

  15. He, Y., Xu, J., Zhou, A.: Local and parallel finite element algorithms for the Navier-Stokes problem. J. Comput. Math. 24(3), 227–238 (2006)

    MathSciNet  Google Scholar 

  16. Jia, S., Xie, H., Xie, M., Xu, F.: A full multigrid method for nonlinear eigenvalue problems. Sci. China Math. 59, 2037–2048 (2016)

    Article  MathSciNet  Google Scholar 

  17. Li, Y., Han, X., Xie, H., You, C.: Local and parallel finite element algorithm based on multilevel discretization for eigenvalue problem. Int. J. Numer. Anal. Model. 13(1), 73–89 (2016)

    MathSciNet  Google Scholar 

  18. Lin, Q., Xie, H.: A multi-level correction scheme for eigenvalue problems. Math. Comp. 84(291), 71–88 (2015)

    Article  MathSciNet  Google Scholar 

  19. Lin, Q., Xie, H., Xu, F.: Multilevel correction adaptive finite element method for semilinear elliptic equation. Appl. Math. 60(5), 527–550 (2015)

    Article  MathSciNet  Google Scholar 

  20. Liu, Q., Hou, Y.: Local and parallel finite element algorithms for time-dependent convection-diffusion equations. Appl. Math. Mech. Engl. Ed. 30, 787–794 (2009)

    Article  MathSciNet  Google Scholar 

  21. Ma, F., Ma, Y., Wo, W.: Local and parallel finite element algorithms based on two-grid discretization for steady Navier-Stokes equations. Appl. Math. Mech. 28(1), 27–35 (2007)

    Article  MathSciNet  Google Scholar 

  22. Ma, Y., Zhang, Z., Ren, C.: Local and parallel finite element algorithms based on two-grid discretization for the stream function form of Navier-Stokes equations. Appl. Math. Comput. 175, 786–813 (2006)

    MathSciNet  Google Scholar 

  23. Shaidurov, V.: Multigrid Methods For Finite Elements. Springer (1995)

  24. Shang, Y., Wang, K.: Local and parallel finite element algorithms based on two-grid discretizations for the transient Stokes equations. Numer. Algorithms 54, 195–218 (2010)

    Article  MathSciNet  Google Scholar 

  25. Shang, Y., He, Y., Luo, Z.: A comparison of three kinds of local and parallel finite element algorithms based on two-grid discretizations for the stationary Navier-Stokes equations. Comput. Fluids 40, 249–257 (2011)

    Article  MathSciNet  Google Scholar 

  26. Tang, Q., Huang, Y.: Local and parallel finite element algorithm based on Oseen-type iteration for the stationary incompressible MHD flow. J. Sci. Comput. 70, 149–174 (2017)

    Article  MathSciNet  Google Scholar 

  27. Watson, E.B., Evans, D.V.: Resonant frequencies of a fluid in containers with internal bodies. J. Engrg. Math. 25(2), 115–135 (1991)

    Article  MathSciNet  Google Scholar 

  28. Xie, H.: A multigrid method for eigenvalue problem. J. Comput. Phys. 274, 550–561 (2014)

    Article  MathSciNet  Google Scholar 

  29. Xu, F., Huang, Q., Ma, H.: Local and parallel multigrid method for semilinear elliptic equations. Appl. Numer. Math. 162, 20–34 (2021)

    Article  MathSciNet  Google Scholar 

  30. Xu, J.: Iterative methods by space decomposition and subspace correction. SIAM Rev. 34(4), 581–613 (1992)

    Article  MathSciNet  Google Scholar 

  31. Xu, J., Zhou, A.: A two-grid discretization scheme for eigenvalue problems. Math. Comput. 70(233), 17–25 (2001)

    Article  MathSciNet  Google Scholar 

  32. Xu, J., Zhou, A.: Local and parallel finite element algorithms based on two-grid discretizations. Math. Comput. 69(231), 881–909 (1999)

    Article  MathSciNet  Google Scholar 

  33. Xu, J., Zhou, A.: Local and parallel finite element algorithms based on two-grid discretizations for nonlinear problems. Adv. Comput. Math. 14, 293–327 (2001)

    Article  MathSciNet  Google Scholar 

  34. Xu, J., Zhou, A.: Local and parallel finite element algorithms for eigenvalue problems. Acta. Math. Appl. Sin. Engl. Ser. 18, 185–200 (2002)

    Article  MathSciNet  Google Scholar 

  35. Xu, J., Zou, J.: Some non-overlapping domain decomposition methods. SIAM Rev. 40(4), 857–914 (1998)

    Article  MathSciNet  Google Scholar 

  36. Yao, C., Li, F., Zhao, Y.: Superconvergence analysis of two-grid FEM for Maxwell’s equations with a thermal effect. Comput. Math. Appl. 79(12), 3378–3393 (2020)

    Article  MathSciNet  Google Scholar 

  37. Yu, J., Shi, F., Zheng, H.: Local and parallel finite element algorithms based on the partition of unity for the Stokes problem. SIAM J. Sci. Comput. 36(5), C547–C567 (2014)

    Article  MathSciNet  Google Scholar 

  38. Zhao, R., Yang, Y., Bi, H.: Local and parallel finite element method for solving the biharmonic eigenvalue problem of plate vibration. Numer. Methods Partial Differ. Equ. 35(2), 851–869 (2019)

    Article  MathSciNet  Google Scholar 

  39. Zheng, H., Yu, J., Shi, F.: Local and parallel finite element algorithm based on the partition of unity for incompressible flows. J. Sci. Comput. 65(2), 512–532 (2015)

    Article  MathSciNet  Google Scholar 

  40. Zheng, H., Shi, F., Hou, Y., Zhao, J., Cao, Y., Zhao, R.: New local and parallel finite element algorithm based on the partition of unity. J. Math. Anal. Appl. 435(1), 1–19 (2016)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Beijing Institute for Scientific and Engineering Computing, Faculty of Science, Beijing University of Technology, Beijing, 100124, People’s Republic of China

    Fei Xu & Bingyi Wang

  2. Center for Applied Mathematics, Tianjin University, Tianjin, 300072, China

    Manting Xie

Authors
  1. Fei Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Bingyi Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Manting Xie
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Manting Xie.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by the Beijing Municipal Natural Science Foundation (Grant No. 1232001) General projects of science and technology plan of Beijing Municipal Education Commission (Grant No. KM202110005011) and the National Natural Science Foundation of China (Grant Nos. 11801021).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, F., Wang, B. & Xie, M. Local and parallel multigrid method for semilinear Neumann problem with nonlinear boundary condition. Numer Algor 96, 185–210 (2024). https://doi.org/10.1007/s11075-023-01643-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-023-01643-5

Keywords

Mathematics Subject Classification (2010)