Skip to main content
Springer Nature Link
Log in

Unconditional long-time stability-preserving second-order BDF fully discrete method for fractional Ginzburg-Landau equation

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

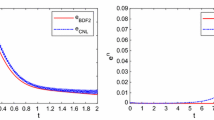
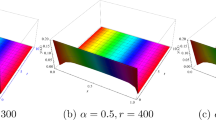
In this paper, we study the long-time stability-preserving properties of the two-step backward differentiation formula (BDF2) fully discrete scheme for the fractional complex Ginzburg-Landau equation. More precisely, we consider the BDF2 time discretization together with a general spatial spectral discretization and show that the numerical scheme can unconditionally preserve the long-time stability in the \(L^2\), \(H^1\), \(H^{1+\alpha }\) and \(H^2\) norms with the aid of the discrete uniform Gronwall lemma. As a special case, we obtain the long-time stability-preserving properties of the fully discrete BDF2 spectral method for the standard complex Ginzburg-Landau equation for the first time. Numerical examples are presented to support our theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Ginzburg, V.L., Landau, L.D.: On the theory of superconductivity. Zh. Eksp. Teor. Fiz. 20, 1064–1082 (1950)

    Google Scholar 

  2. Gao, H.J., Lin, G.G., Duan, J.Q.: Asymptotics for the generalized two-dimensional Ginzburg-Landau equation. J. Math. Anal. Appl. 247, 198–216 (2000)

    Article  MathSciNet  Google Scholar 

  3. Huo, Z.H., Jia, Y.L.: Global well-posedness for the generalized 2D Ginzburg-Landau equation. J. Differential Equations 247, 260–276 (2009)

    Article  MathSciNet  Google Scholar 

  4. Liu, W.J., Yu, W.T., Yang, C.Y., Liu, M.L., Zhang, Y.J., Lei, M.: Analytic solutions for the generalized complex Ginzburg-Landau equation in fiber lasers. Nonlinear Dynam. 89, 2933–2939 (2017)

    Article  MathSciNet  Google Scholar 

  5. Takáč, P., Jüngel, A.: A nonstiff Euler discretization of the complex Ginzburg-Landau equation in one space dimension. SIAM J. Num. Anal. 38, 292–328 (2000)

    Article  MathSciNet  Google Scholar 

  6. Lü, S.J., Lu, Q.S.: Fourier spectral approximation to long-time behavior of three dimensional Ginzburg-Landau type equation. Adv. Comput. Math. 27, 293–318 (2007)

    Article  MathSciNet  Google Scholar 

  7. Degond, P., Jin, S., Tang, M.: On the time splitting spectral method for the complex Ginzburg-Landau equation in the large time and space scale limit. SIAM J. Sci. Comput. 30, 2466–2487 (2008)

    Article  MathSciNet  Google Scholar 

  8. Tarasov, V.E., Zaslavsky, G.M.: Fractional Ginzburg-Landau equation for fractal media. Phys. A 354, 249–261 (2005)

    Article  Google Scholar 

  9. Tarasov, V.E., Zaslavsky, G.M.: Fractional dynamics of coupled oscillators with long-range interaction. Chaos 16, 023110 (2006)

    Article  MathSciNet  Google Scholar 

  10. Mvogo, A., Tambue, A., Ben-Bolie, G.H., Kofan, T.C.: Localized numerical impulse solutions in diffuse neural networks modeled by the complex fractional Ginzburg-Landau equation. Commun. Nonlinear Sci. Numer. Simul. 39, 396–410 (2016)

    Article  MathSciNet  Google Scholar 

  11. Pu, X.K., Guo, B.L.: Well-posedness and dynamics for the fractional Ginzburg-Landau equation. Appl. Anal. 93, 318–334 (2013)

    Article  MathSciNet  Google Scholar 

  12. Guo, B.L., Pu, X.K., Huang, F.H.: Fractional partial differential equations and their numerical solutions. Science Press, Beijing (2011)

    Google Scholar 

  13. Lu, H. , Lü, S.J., Feng, Z. S.: Asymptotic dynamics of 2D fractional complex Ginzburg-Landau equation. Int. J. Bifur. Chaos. 23, 12 (2013)

  14. Wang, P.D., Huang, C.M.: An implicit midpoint difference scheme for the fractional Ginzburg-Landau equation. J. Comput. Phys. 312, 31–49 (2016)

    Article  MathSciNet  Google Scholar 

  15. Wang, P.D., Huang, C.M.: An efficient fourth-order in space difference scheme for the nonlinear fractional Ginzburg-Landau equation. BIT 58, 783–805 (2018)

    Article  MathSciNet  Google Scholar 

  16. Hao, Z.P., Sun, Z.Z.: A linearized high-order difference scheme for the fractional Ginzburg-Landau equation. Numer. Methods Partial Differential Equations 33, 105–124 (2017)

    Article  MathSciNet  Google Scholar 

  17. He, D., Pan, K.J.: An unconditionally stable linearized difference scheme for the fractional Ginzburg-Landau equation. Numer. Algorithms 79, 899–925 (2018)

    Article  MathSciNet  Google Scholar 

  18. Zhang, Q.F., Lin, X.M., Pan, K.J., Ren, Y.Z.: Linearized ADI schemes for two-dimensional space-fractional nonlinear Ginzburg-Landau equation. Comput. Math. Appl. 80, 1201–1220 (2020)

    Article  MathSciNet  Google Scholar 

  19. Li, M., Huang, C.M., Wang, N.: Galerkin finite element method for the nonlinear fractional Ginzburg-Landau equation. Appl. Numer. Math. 118, 131–149 (2017)

    Article  MathSciNet  Google Scholar 

  20. Zhang, Z., Li, M., Wang, Z.: A linearized Crank-Nicolson Galerkin FEMs for the nonlinear fractional Ginzburg-Landau equation. Appl. Anal. 98, 2648–2667 (2019)

    Article  MathSciNet  Google Scholar 

  21. Lu, H., Lü, S., Zhang, M.: Fourier spectral approximations to the dynamics of 3D fractional complex Ginzburg-Landau equation. Discrete Contin. Dyn. Syst. 37, 2539–2564 (2017)

    Article  MathSciNet  Google Scholar 

  22. Lu, H., Zhang, M.: The spectral method for long-time behavior of a fractional power dissipative system. Taiwanese J. Math. 22, 453–483 (2018)

    Article  MathSciNet  Google Scholar 

  23. Zeng, W., Xiao, A.G., Li, X.Y.: Error estimate of Fourier pseudo-spectral method for multidimensional nonlinear complex fractional Ginzburg-Landau equations. Appl. Math. Lett. 93, 40–45 (2019)

    Article  MathSciNet  Google Scholar 

  24. Mazja, V.G.: Sobolev space, Springer-Verlag (1985)

  25. Wang, W.S., Huang, Y.: Analytical and numerical dissipativity for the space-fractional Allen-Cahn equation. Math. Comput. Simul. 207, 80–96 (2023)

    Article  MathSciNet  Google Scholar 

  26. Wang, W.S.: Dissipativity of the linearly implicit Euler scheme for Navier-Stokes equations with delay. Numer. Methods Partial differential equations 33, 2114–2140 (2017)

    Article  MathSciNet  Google Scholar 

  27. Wang, W.S., Wang, Z., Li, Z.X.: Long time \(H^\alpha \) stability of a classical scheme for Cahn-Hilliard equation with polynomial nonlinearity. Appl. Numer. Math. 165, 35–55 (2021)

    Article  MathSciNet  Google Scholar 

  28. Wang, X.M.: An efficient second order in time scheme for approximating long time statistical properties of the two dimensional Navier-Stokes equations. Numer. Math. 121, 753–779 (2012)

    Article  MathSciNet  Google Scholar 

Download references

Funding

This study was funded by the National Natural Science Foundation of China (Grant Nos. 12271367), Shanghai Science and Technology Planning Projects (Grant No. 20JC1414200), Natural Science Foundation of Shanghai (Grant No. 20ZR1441200), and The Scientific Research Fund of Hunan Provincial Education Department (Grant No. 22B0879).

Author information

Authors and Affiliations

  1. Department of Mathematics, Shanghai Normal University, Shanghai, 200234, China

    Yi Huang, Wansheng Wang & Yanming Zhang

  2. School of Mathematics and Statistics, Hunan First Normal University, Changsha, 410006, China

    Yanming Zhang

Authors
  1. Yi Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Wansheng Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yanming Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Y. Huang and W. S. Wang wrote the main manuscript text and Y. M. Zhang prepared the figures. All authors reviewed the manuscript.

Corresponding author

Correspondence to Wansheng Wang.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, Y., Wang, W. & Zhang, Y. Unconditional long-time stability-preserving second-order BDF fully discrete method for fractional Ginzburg-Landau equation. Numer Algor 97, 167–189 (2024). https://doi.org/10.1007/s11075-023-01699-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-023-01699-3

Keywords

Mathematics Subject Classification (2010)