Skip to main content
Springer Nature Link
Log in

Jacobian-free explicit multiderivative general linear methods for hyperbolic conservation laws

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

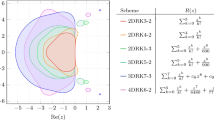
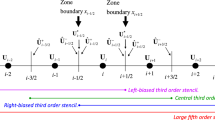
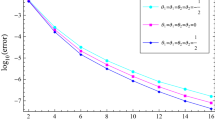
Abstract

We study explicit strong stability preserving (SSP) multiderivative general linear methods (MDGLMs) for the numerical solution of hyperbolic conservation laws. Sufficient conditions for MDGLMs up to four derivatives to be SSP are determined. In this work, we describe the construction of two external stage explicit SSP MDGLMs based on Taylor series conditions, and present examples of constructed methods up to order nine and three internal stages along with their SSP coefficients. It is difficult to apply these methods directly to the discretization of partial differential equations, as higher-order flux derivatives must be calculated analytically. We hence use a Jacobian-free approach based on the recent development of explicit Jacobian-free multistage multiderivative solvers (Chouchoulis et al. J. Sci. Comput. 90, 96, 2022) that provides a practical application of MDGLMs. To show the capability of our novel methods in achieving the predicted order of convergence and preserving required stability properties, several numerical test cases for scalar and systems of equations are provided.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Algorithm 1
Algorithm 2
Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Data Availability

No datasets were generated or analyzed during the current study.

Notes

  1. The dot \((\cdot )\) stands for the time derivative d/dt, whereas the prime \((')\) stands for the Jacobian of the vector-valued \(\varPhi \) w.r.t. y.

References

  1. Abdi, A.: Construction of high-order quadratically stable second-derivative general linear methods for the numerical integration of stiff ODEs. J. Comput. Appl. Math. 303, 218–228 (2016)

    MathSciNet  Google Scholar 

  2. Abdi, A., Behzad, B.: Efficient Nordsieck second derivative general linear methods: construction and implementation. Calcolo 55(28), 1–16 (2018)

    MathSciNet  Google Scholar 

  3. Abdi, A., Braś, M., Hojjati, G.: On the construction of second derivative diagonally implicit multistage integration methods. Appl. Numer. Math. 76, 1–18 (2014)

    MathSciNet  Google Scholar 

  4. Abdi, A., Conte, D.: Implementation of second derivative general linear methods. Calcolo 57, 20 (2020)

    MathSciNet  Google Scholar 

  5. Butcher, J.C.: On the convergence of numerical solutions to ordinary differential equations. Math. Comput. 20, 1–10 (1966)

    MathSciNet  Google Scholar 

  6. Butcher, J.C.: Numerical methods for ordinary differential equations. Wiley, New York (2016)

    Google Scholar 

  7. Butcher, J.C., Hojjati, G.: Second derivative methods with RK stability. Numer. Algorithms 40, 415–429 (2005)

    MathSciNet  Google Scholar 

  8. Califano, G., Izzo, G., Jackiewicz, Z.: Strong stability preserving general linear methods with Runge-Kutta stability. J. Sci. Comput. 76, 943–968 (2018)

    MathSciNet  Google Scholar 

  9. Carrillo, H., Parés, C.: Compact approximate Taylor methods for systems of conservation laws. J. Sci. Comput. 80(3), 1832–1866 (2019)

    MathSciNet  Google Scholar 

  10. Cash, J.R.: Second derivative extended backward differentiation formulas for the numerical integration of stiff systems. SIAM J. Numer. Anal. 18, 21–36 (1981)

    MathSciNet  Google Scholar 

  11. Chouchoulis, J., Schütz, J., Zeifang, J.: Jacobian-free explicit multiderivative Runge-Kutta methods for hyperbolic conservation laws. J. Sci. Comput. 90, 96 (2022)

    MathSciNet  Google Scholar 

  12. Chan, R.P.K., Tsai, A.Y.J.: On explicit two-derivative Runge-Kutta methods. Numer. Algorithms 53, 171–194 (2010)

    MathSciNet  Google Scholar 

  13. Cheng, J.B., Toro, E.F., Jiang, S., Tang, W.: A sub-cell WENO reconstruction method for spatial derivatives in the ADER scheme. J. Comput. Phys. 251, 53–80 (2013)

    MathSciNet  Google Scholar 

  14. Christlieb, A.J., Gottlieb, S., Grant, Z., Seal, D.C.: Explicit strong stability preserving multistage two-derivative time-stepping schemes. J. Sci. Comput. 68, 914–942 (2016)

    MathSciNet  Google Scholar 

  15. Dahlquist, G.: A special stability problem for linear multistep methods. BIT 3, 27–43 (1963)

    MathSciNet  Google Scholar 

  16. Dumbser, M., Balsara, D.S., Toro, E.F., Munz, C.-D.: A unified framework for the construction of one-step finite volume and discontinuous Galerkin schemes on unstructured meshes. J. Comput. Phys. 227(18), 8209–8253 (2008)

    MathSciNet  Google Scholar 

  17. Dumbser, M., Enaux, C., Toro, E.F.: Finite volume schemes of very high order of accuracy for stiff hyperbolic balance laws. J. Comput. Phys. 227(8), 3971–4001 (2008)

    MathSciNet  Google Scholar 

  18. Dumbser, M., Fambri, F., Tavelli, M., Bader, M., Weinzierl, T.: Efficient implementation of ADER discontinuous Galerkin schemes for a scalable hyperbolic PDE engine. Axioms 7(3), 63 (2018)

    Google Scholar 

  19. Gottlieb, S.: On high order strong stability preserving Runge-Kutta and multi step time discretizations. J. Sci. Comput. 25, 105–128 (2005)

    MathSciNet  Google Scholar 

  20. Gottlieb, S., Ketcheson, D.I., Shu, C.-W.: Strong stability preserving Runge-Kutta and multistep time discretizations. World Scientific, Hackensack (2011)

    Google Scholar 

  21. Gottlieb, S., Shu, C.-W., Tadmor, E.: Strong stability-preserving high-order time discretization methods. SIAM Rev. 43, 89–112 (2001)

    MathSciNet  Google Scholar 

  22. Grant, Z., Gottlieb, S., Seal, D.C.: A strong stability preserving analysis for explicit multistage two-derivative time-stepping schemes based on Taylor series conditions. Commun. Appl. Math. Comput. 1, 21–59 (2019)

    MathSciNet  Google Scholar 

  23. Hairer, E., Wanner, G.: Solving ordinary differential equations II: stiff and differential-algebraic problems. Springer, Berlin (2010)

    Google Scholar 

  24. Higueras, I.: Representations of Runge-Kutta methods and strong stability preserving methods. SIAM J. Numer. Anal. 43, 924–948 (2005)

    MathSciNet  Google Scholar 

  25. Hundsdorfer, W., Ruuth, S.J.: On monotonicity and boundedness properties of linear multistep methods. Math. Comput. 75, 655–672 (2005)

    MathSciNet  Google Scholar 

  26. Izzo, G., Jackiewicz, Z.: Strong stability preserving general linear methods. J. Sci. Comput. 65, 271–298 (2015)

    MathSciNet  Google Scholar 

  27. Jackiewicz, Z.: General linear methods for ordinary differential equations. Wiley, Hoboken (2009)

    Google Scholar 

  28. Ketcheson, D.I., Gottlieb, S., Macdonald, C.B.: Strong stability preserving two-step Runge-Kutta methods. SIAM J. Numer. Anal. 49, 2618–2639 (2011)

    MathSciNet  Google Scholar 

  29. Lax, P., Wendroff, B.: Systems of conservation laws. Commun. Pure Appl. Math. 13(2), 217–237 (1960)

    Google Scholar 

  30. LeVeque, R.J.: Numerical methods for conservation laws. Birkhäuser, Basel (1990)

    Google Scholar 

  31. Moradi, A., Farzi, J., Abdi, A.: Strong stability preserving second derivative general linear methods. J. Sci. Comput. 81, 392–435 (2019)

    MathSciNet  Google Scholar 

  32. Moradi, A., Abdi, A., Farzi, J.: Strong stability preserving second derivative general linear methods with Runge-Kutta stability. J. Sci. Comput. 85(1), 1–39 (2020)

    MathSciNet  Google Scholar 

  33. Moradi, A., Abdi, A., Farzi, J.: Strong stability preserving second derivative diagonally implicit multistage integration methods. Appl. Numer. Math. 150, 536–558 (2020)

    MathSciNet  Google Scholar 

  34. Moradi, A., Sharifi, M., Abdi, A.: Transformed implicit-explicit second derivative diagonally implicit multistage integration methods with strong stability preserving explicit part. Appl. Numer. Math. 156, 14–31 (2020)

    MathSciNet  Google Scholar 

  35. Moradi, A., Abdi, A., Farzi, J.: Strong stability preserving diagonally implicit multistage integration methods. Appl. Numer. Math. 150, 536–558 (2020)

    MathSciNet  Google Scholar 

  36. Moradi, A., Abdi, A., Hojjati, G.: High order explicit second derivative methods with strong stability properties based on Taylor series conditions. ANZIAM J., 1–28 (2022)

  37. Moradi, A., Abdi, A., Hojjati, G.: Strong stability preserving second derivative general linear methods based on Taylor series conditions for discontinuous Galerkin discretizations. J. Sci. Comput. 98(20), 1–21 (2024)

    MathSciNet  Google Scholar 

  38. Ökten Turacı, M., Öziş, T.: Derivation of three-derivative Runge-Kutta methods. Numer. Algorithms 74(1), 247–265 (2017)

    MathSciNet  Google Scholar 

  39. Qin, X., Jiang, Z., Yu, J., Huang, L., Yan, C.: Strong stability-preserving three-derivative Runge-Kutta methods. Comput. Appl. Math. 42(171), 1–24 (2023)

    MathSciNet  Google Scholar 

  40. Schütz, J., Seal, D.C., Jaust, A.: Implicit multiderivative collocation solvers for linear partial differential equations with discontinuous Galerkin spatial discretizations. J. Sci. Comput. 73, 1145–1163 (2017)

    MathSciNet  Google Scholar 

  41. Seal, D.C., Gülü, Y., Christlieb, A.: High-order multiderivative time integrators for hyperbolic conservation laws. J. Sci. Comput. 60, 101–140 (2014)

    MathSciNet  Google Scholar 

  42. Schwartzkopff, T., Dumbser, M., Munz, C.-D.: ADER: a high-order approach for linear hyperbolic systems in 2D. J. Sci. Comput. 17, 231–240 (2002)

    MathSciNet  Google Scholar 

  43. Shu, C.-W.: Total-variation diminishing time discretizations. J. Sci. Comput. 9, 1073–1084 (1988)

    MathSciNet  Google Scholar 

  44. Shu, C.-W.: Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In: Quarteroni, A. (ed.) Advanced numerical approximation of nonlinear hyperbolic equations, pp. 325–432. Springer, Berlin (1998)

    Google Scholar 

  45. Titarev, V.A., Toro, E.F.: ADER: arbitrary high order Godunov approach. J. Sci. Comput. 17(1), 609–618 (2002)

    MathSciNet  Google Scholar 

  46. Titarev, V.A., Toro, E.F.: ADER schemes for three-dimensional non-linear hyperbolic systems. J. Comput. Phys. 204(2), 715–736 (2005)

    MathSciNet  Google Scholar 

  47. Toro, E.F., Titarev, V.A.: Derivative Riemann solvers for systems of conservation laws and ADER methods. J. Comput. Phys. 212, 150–165 (2006)

    MathSciNet  Google Scholar 

  48. Whitham, G.: Linear and nonlinear waves. A Wiley Series of Texts, Monographs and Tracts. Wiley, New York, Pure and Applied Mathematics (2011)

    Google Scholar 

  49. Zhang, X., Shu, C.-W.: On maximum-principle-satisfying high order schemes for scalar conservation laws. J. Comput. Phys. 229, 3091–3120 (2010)

    MathSciNet  Google Scholar 

  50. Zorìo, D., Baeza, A., Mulet, P.: An approximate Lax-Wendroff-type procedure for high order accurate schemes for hyperbolic conservation laws. J. Sci. Comput. 71, 246–273 (2017)

    MathSciNet  Google Scholar 

Download references

Funding

R. D’Ambrosio is supported by GNCS-INDAM project and PRIN2017-MIUR project 2017JYCLSF “Structure preserving approximation of evolutionary problems.”

Author information

Authors and Affiliations

  1. Department of Information Engineering and Computer Science and Mathematics, University of L’Aquila, L’Aquila, Italy

    Afsaneh Moradi & Raffaele D’Ambrosio

  2. Faculty of Sciences & Data Science Institute, Hasselt University, Agoralaan Gebouw D, 3590 Diepenbeek, Hasselt, Belgium

    Jeremy Chouchoulis & Jochen Schütz

Authors
  1. Afsaneh Moradi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jeremy Chouchoulis
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Raffaele D’Ambrosio
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jochen Schütz
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Afsaneh Moradi: conceptualization, formal analysis, investigation, methodology, software, validation, visualization, writing—orginal draft, writing—review and editing. Jeremy Choichoulis: conceptualization, formal analysis, investigation, methodology, software, validation, visualization, writing—review and editing. Jochen Schutz: conceptualization, formal analysis, investigation, methodology, software, supervision, writing—review and editing. Rafeale D’Ambrosio: conceptualization, formal analysis, investigation, methodology, software, supervision, writing—review and editing.

Corresponding author

Correspondence to Afsaneh Moradi.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendices

A   Coefficients of third-derivative GLMs

Here, we give the coefficient matrices of the constructed third-derivative GLMs for \(s=2\) and \(s=3\). The coefficient matrices of two stage methods take the form

and three stage methods take the following form

1. SSP 3DGLM4-2

$$\begin{array}{llll} a^{\{1\}}_{21} = 0.481524563110426, &{} a^{\{2\}}_{21} = 0.107666492481270, &{} a^{\{3\}}_{21} = 0.021992397120078,&{} b^{\{1\}}_{11} = 0.498435904450369, \\ b^{\{1\}}_{12} = 0.522530753430964, &{} b^{\{1\}}_{21} = 0.410124141823035, &{} b^{\{1\}}_{22} = 0.463432449474462, &{} b^{\{2\}}_{11} = 0.095786801825143, \\ b^{\{2\}}_{12} = 0.152075022730067, &{} b^{\{2\}}_{21} = 0.137529315089621, &{} b^{\{2\}}_{22} = 0.088062569968302, &{} b^{\{3\}}_{11} = 0.018694337702556,\\ b^{\{3\}}_{12} = 0.027732589352203, &{} b^{\{3\}}_{21} = 0.015749712492286, &{} b^{\{3\}}_{22} = 0.005659319478742, &{} u_{11} = 0.935650184213693, \\ u_{12} = 0.064349815786307, &{} u_{21} = 0.886315321544333,&{} u_{22} = 0.113684678455667, &{} v = 0.142233555463516, \\ c_1 = 0.525747892280569, &{} w_{10} = 1.0, &{} w_{11} = 0.535233702910286,&{} w_{12} = 0.136943388092356, \\ w_{13} = 0.027743278545692, &{} w_{14} = 0.002690489400088, &{}w_{20} = 1.0, &{} w_{21} = 0.387823636326451, \\ w_{22} = 0.156555488157499, &{} w_{23} = -0.027002414204259, &{} w_{24} = 0.010351227670424. &{} \end{array}$$

2. SSP 3DGLM5-2

$$\begin{array}{llll} a^{\{1\}}_{21} = 0.444563089345968, &{} a^{\{2\}}_{21} = 0.220433797971554, &{} a^{\{3\}}_{21} = 0.047199086888770, &{}b^{\{1\}}_{11} = 0.677030364676214, \\ b^{\{1\}}_{12} = 0.109344513124094, &{} b^{\{1\}}_{21} = 0.600001026747633, &{} b^{\{1\}}_{22} = 0.643878289010242, &{} b^{\{2\}}_{11} = 0.187812461430404, \\ b^{\{2\}}_{12} = 0.167420842533560, &{} b^{\{2\}}_{21} = 0.335797629018218, &{} b^{\{2\}}_{22} = 0.027367894432842, &{} b^{\{3\}}_{11} = 0.019973582828875,\\ b^{\{3\}}_{12} = 0.014734064127359, &{} b^{\{3\}}_{21} = 0.076346090518484, &{} b^{\{3\}}_{22} = 0.007807990410220, &{} u_{11} = 0.691735860871995, \\ u_{12} = 0.308264139128005, &{} u_{21} = 0.362379132344019,&{}u_{22} = 0.637620867655981, &{} v = 0.466935628326092,\\ c_1 = 0.404754745681296, &{} w_{10} = 1.0, &{} w_{11} = 0.263722533967065,&{} w_{12} = 0.065333656992811, \\ w_{13} = 0.027169926386350, &{} w_{14} = 0.002545864356240, &{}w_{15} = -0.001260324593837, &{} w_{20} = 1.0, \\ w_{21} = 0.721226971924633, &{}w_{22} = 0.119117224325207, &{} w_{23} = -0.025117506961899, &{}w_{24} = -0.002085128124951, \\ w_{25} = 0.003121799371033.&{}&{}&{} \end{array}$$

3. SSP 3DGLM6-3

$$\begin{array}{llll} a^{\{1\}}_{21} = 0.315517321907129, &{} a^{\{1\}}_{31} = 0.758864601103138, &{} a^{\{1\}}_{32} = 0.067336415726727,&{} a^{\{2\}}_{21} = 0.076494847917531, \\ a^{\{2\}}_{31} = 0.165996492414755, &{} a^{\{2\}}_{32} = 0.131818841412823, &{} a^{\{3\}}_{21} = 0.026098214000471,&{} a^{\{3\}}_{31} = 0.010407236225120, \\ a^{\{3\}}_{32} = 0.011694043676070, &{} b^{\{1\}}_{11} = 0.466407769409968, &{} b^{\{1\}}_{12} = 0.588029782942878,&{} b^{\{1\}}_{13} = 0.090753993408768,\\ b^{\{1\}}_{21} = 0.714352536776548, &{} b^{\{1\}}_{22} = 0.004057520548612, &{} b^{\{1\}}_{23} = 0.043314290009643,&{} b^{\{2\}}_{11} = 0.101470387228004, \\ b^{\{2\}}_{12} = 0.309600095382871, &{} b^{\{2\}}_{13} = 0.003137222126554, &{} b^{\{2\}}_{21} = 0.208922227866803,&{} b^{\{2\}}_{22} = 0.036586254679526,\\ b^{\{2\}}_{23} = 0.023218417766703, &{} b^{\{3\}}_{11} = 0.016855407713879, &{} b^{\{3\}}_{12} = 0.051517368037844,&{} b^{\{3\}}_{13} = 0.001065531053630,\\ b^{\{3\}}_{21} = 0.035888517238621, &{} b^{\{3\}}_{22} = 0.000525893188072, &{} b^{\{3\}}_{23} = 0.007526287669863,&{} u_{11} = 0.429393552342717, \\ u_{12} = 0.570606447657283, &{} u_{21} = 0.714766096918914, &{} u_{22} = 0.285233903081086, &{} u_{31} = 0.373124486427176, \\ u_{32} = 0.626875513572824, &{} v = 0.378628332116197, &{} c_1 = 0.195376324234861, &{} c_2 = 0.620324656318555,\\ w_{10} = 1.0, &{} w_{11} = 0.414185180122275,&{} w_{12} = 0.089420710803121, &{} w_{13} = -0.015802200386162, \\ w_{14} = -0.001623142712040,&{} w_{15} = 0.000303750873378, &{} w_{16} = 0.218129334015903, &{} w_{20} = 1.0, \\ w_{21} = 0.030717981695463, &{} w_{22} = -0.033842454301531,&{} w_{23} = 0.014069844764195, &{}w_{24} = 0.001327849153771, \\ w_{25} = -0.000224421436006, &{}w_{26} = 0.217923761039387.&{} &{} \end{array}$$

4. SSP 3DGLM7-3

$$\begin{array}{llll} a^{\{1\}}_{21} = 0.379665884421877, &{} a^{\{1\}}_{31} = 0.515488221507126, &{}a^{\{1\}}_{32} = 0.008239732993902,&{} a^{\{2\}}_{21} = 0.060210073470162, \\ a^{\{2\}}_{31} = 0.114667967793747, &{} a^{\{2\}}_{32} = 0.010050929935034, &{} a^{\{3\}}_{21} = 0.027175182796611,&{} a^{\{3\}}_{31} = 0.093175561916561, \\ a^{\{3\}}_{32} = 0.008173511911974, &{} b^{\{1\}}_{11} = 1.107792953001359, &{} b^{\{1\}}_{12} = 0.090330329859403,&{} b^{\{1\}}_{13} = 0.000000066635348,\\ b^{\{1\}}_{21} = 0.664653168823024, &{} b^{\{1\}}_{22} = 0.309711371128129, &{} b^{\{1\}}_{23} = 0.015546721568938,&{} b^{\{2\}}_{11} = 0.189649927487829, \\ b^{\{2\}}_{12} = 0.600387177342980, &{} b^{\{2\}}_{13} = 0.000000000094460, &{} b^{\{2\}}_{21} = 0.107129004361048,&{} b^{\{2\}}_{22} = 0.214103657229089, \\ b^{\{2\}}_{23} = 0.018964113794848, &{} b^{\{3\}}_{11} = 0.003171262661914, &{} b^{\{3\}}_{12} = 0.067436297519191,&{} b^{\{3\}}_{13} = 0.000000000076816,\\ b^{\{3\}}_{21} = 0.006076703572795, &{} b^{\{3\}}_{22} = 0.000052086287613, &{} b^{\{3\}}_{23} = 0.015421809057899,&{} u_{11} = 0.050799054224709, \\ u_{12} = 0.949200945775291, &{} u_{21} = 0.271811785253415, &{} u_{22} = 0.728188214746585, &{} u_{31} = 0.848358688706512, \\ u_{32} = 0.151641311293488, &{} v = 0.951545856064458, &{} c_1 = 0.310210488718125, &{} c_2 = 0.735893895336771,\\ w_{10} = 1.0, &{} w_{11} = 0.507845599546811,&{} w_{12} = 0.239955454479258, &{} w_{13} = -0.006520488569236, \\ w_{14} = -0.005551486351131, &{} w_{15} = 0.000113698479916, &{} w_{16} = 0.000223765806822, &{} w_{17} = 1.999940921849224, \\ w_{20} = 1.0,&{}w_{21} = 0.299633511570792, &{} w_{22} = 0.037848427850458,&{} w_{23} = 0.005590515047944, \\ w_{24} = 0.000703599013788,&{} w_{25} = 0.000019134996526, &{} w_{26} = -0.000010671520193, &{} w_{27} = 2.0. \end{array}$$

B   Coefficients of Fourth-derivative GLMs

Here, we give the coefficients matrices of the constructed fourth-derivative GLMs for \(s=2\) and \(s=3\). The coefficient matrices of two stage methods take the form

and three stage methods take the following form

1. SSP 4DGLM4-2

$$\begin{array}{llll} a^{\{1\}}_{21} = 0.492502401255857, &{} a^{\{2\}}_{21} = 0.121549058540707, &{} a^{\{3\}}_{21} = 0.019860332137553, &{} a^{\{4\}}_{21} = 0.002469334621926,\\ b^{\{1\}}_{11} = 0.493035280152582, &{} b^{\{1\}}_{12} = 0.519129890196680, &{} b^{\{1\}}_{21} = 0.492159016664885, &{} b^{\{1\}}_{22} = 0.507134722289626,\\ b^{\{2\}}_{11} = 0.120822362679484, &{} b^{\{2\}}_{12} = 0.118796068553098, &{} b^{\{2\}}_{21} = 0.121514758761671, &{} b^{\{2\}}_{22} = 0.129069521144118,\\ b^{\{3\}}_{11} = 0.019733454185988, &{} b^{\{3\}}_{12} = 0.020130886150193, &{} b^{\{3\}}_{21} = 0.019811609177391, &{} b^{\{3\}}_{22} = 0.021899025203918,\\ b^{\{4\}}_{11} = 0.002452844681870, &{} b^{\{4\}}_{12} = 0.002512408254589, &{} b^{\{4\}}_{21} = 0.002463116135828, &{} b^{\{4\}}_{22} = 0.002754839201374,\\ u_{11} = 0.043647614240132, &{} u_{12} = 0.956352385759868, &{} u_{21} = 0.054763091495361, &{} u_{22} = 0.945236908504639,\\ v = 0.945129564550485, &{} c_1 = 0.507354526641232, &{} w_{10}= 1.0, &{} w_{11} = 0.519664150763746, \\ w_{12} = 0.117804247188642, &{} w_{13} = 0.020428440495935, &{} w_{14} = 0.002458895114308,&{}w_{20} = 1.0, \\ w_{21} = 0.506792719368996, &{} w_{22} = 0.129201783102532, &{} w_{23} = 0.021827294362888, &{} w_{24} = 0.002774578642803. \end{array}$$

2. SSP 4DGLM5-2

$$\begin{array}{llll} a^{\{1\}}_{21} = 0.500492666826293, &{} a^{\{2\}}_{21} = 0.114756600078513, &{} a^{\{3\}}_{21} = 0.018148178751572, &{} a^{\{4\}}_{21} = 0.002714589878061,\\ b^{\{1\}}_{11} = 0.431186537508394, &{} b^{\{1\}}_{12} = 0.404171392100681, &{} b^{\{1\}}_{21} = 0.483662234321112, &{} b^{\{1\}}_{22} = 0.560179604710392,\\ b^{\{2\}}_{11} = 0.081227126476428, &{} b^{\{2\}}_{12} = 0.047086826677170, &{} b^{\{2\}}_{21} = 0.109480320931676, &{} b^{\{2\}}_{22} = 0.135274055565348,\\ b^{\{3\}}_{11} = 0.013178225742208, &{} b^{\{3\}}_{12} = 0.008882729874764, &{} b^{\{3\}}_{21} = 0.017492912408121, &{} b^{\{3\}}_{22} = 0.025272005673387,\\ b^{\{4\}}_{11} = 0.001589026148517, &{} b^{\{4\}}_{12} = 0.000129548838296, &{} b^{\{4\}}_{21} = 0.002446465182670, &{} b^{\{4\}}_{22} = 0.003740837321860,\\ u_{11} = 0.088185135295424, &{} u_{12} = 0.911814864704576, &{} u_{21} = 0.176145583277641, &{} u_{22} = 0.823854416722359, \\ v = 0.789711162108572, &{} c_1 = 0.517845671243588, &{} w_{10}= 1.0,&{} w_{11} = 0.327746943580494,\\ w_{12} = 0.050980139124519, &{} w_{13} = 0.011125839350588, &{} w_{14} = -0.001282009647015, &{} w_{15} = 0.000603507965945,\\ w_{20} = 1.0,&{} w_{21} = 0.536230853002924, &{} w_{22} = 0.142119178095184, &{} w_{23} = 0.024306987806757, \\ w_{24} = 0.003410108652328, &{} w_{25} = 0.000281973075456. &{}&{} \end{array}$$

3. SSP 4DGLM6-2

$$\begin{array}{llll} a^{\{1\}}_{21} = 0.517293370447585, &{} a^{\{2\}}_{21} = 0.133925352925481, &{} a^{\{3\}}_{21} = 0.027371115505543, &{} a^{\{4\}}_{21} = 0.004940436426576,\\ b^{\{1\}}_{11} = 0.562577084182751, &{} b^{\{1\}}_{12} = 0.421763934840916, &{} b^{\{1\}}_{21} = 0.572954574408108, &{} b^{\{1\}}_{22} = 0.478728558134980,\\ b^{\{2\}}_{11} = 0.163935914431203, &{} b^{\{2\}}_{12} = 0.100241069539339, &{} b^{\{2\}}_{21} = 0.170412942747712, &{} b^{\{2\}}_{22} = 0.165570428503403,\\ b^{\{3\}}_{11} = 0.035658092350845, &{} b^{\{3\}}_{12} = 0.016327465256022, &{} b^{\{3\}}_{21} = 0.037215832658113, &{} b^{\{3\}}_{22} = 0.035849937970705,\\ b^{\{4\}}_{11} = 0.005287177412273, &{} b^{\{4\}}_{12} = 0.002944889939538, &{} b^{\{4\}}_{21} = 0.006694878863016, &{} b^{\{4\}}_{22} = 0.000000025053928,\\ u_{11} = 0.991894960507822, &{} u_{12} = 0.008105039492178, &{} u_{21} = 0.677452760618707, &{} u_{22} = 0.322547239381293, \\ v = 0.232528801933385, &{} c_1 = 0.461531427232185, &{} w_{10}= 1.0, &{} w_{11} = 0.460985616742624, \\ w_{12} = 0.105968926131271, &{} w_{13} = 0.016230449697124, &{} w_{14} = 0.001904410077557,&{} w_{15} = 0.000179896607685,\\ w_{16} = 0.000011946083550,&{}w_{20} = 1.0, &{} w_{21} = 0.528327730262044, &{} w_{22} = 0.172187361061285, \\ w_{23} = 0.035327454889158, &{} w_{24} = 0.000197418142938, &{} w_{25} = 0.000484463733041, &{} w_{26} = 0.000194265652679. \end{array}$$

4. SSP 4DGLM7-2

$$\begin{array}{llll} a^{\{1\}}_{21} = 0.499507160885063, &{} a^{\{2\}}_{21} = 0.119968933288827, &{} a^{\{3\}}_{21} = 0.017081896566529, &{} a^{\{4\}}_{21} = 0.004031320198658,\\ b^{\{1\}}_{11} = 0.666614451332563, &{} b^{\{1\}}_{12} = 0.303306256194171, &{} b^{\{1\}}_{21} = 0.576409644843040, &{} b^{\{1\}}_{22} = 0.462190555937428,\\ b^{\{2\}}_{11} = 0.183560532895898, &{} b^{\{2\}}_{12} = 0.155207228786631, &{} b^{\{2\}}_{21} = 0.259780581201447 , &{} b^{\{2\}}_{22} = 0.034723177133322,\\ b^{\{3\}}_{11} = 0.031183451078632, &{} b^{\{3\}}_{12} = 0.041000165610189, &{} b^{\{3\}}_{21} = 0.057101861689900 , &{} b^{\{3\}}_{22} = 0.010915027907463, \\ b^{\{4\}}_{11} = 0.001433739889497, &{} b^{\{4\}}_{12} = 0.004322242467946, &{} b^{\{4\}}_{21} = 0.001529153305801, &{} b^{\{4\}}_{22} = 0.002575963845641,\\ u_{11} = 0.618158814106136, &{} u_{12} = 0.381841185893864, &{} u_{21} = 0.688026611571673 , &{} u_{22} = 0.311973388428327, \\ v = 0.437966138773607, &{} c_1 = 0.505291324039624, &{} w_{10}= 1.0, &{} w_{11} = 0.479066664889029,\\ w_{12} = 0.127521779354434, &{} w_{13} = 0.041705623460671, &{} w_{14} = 0.003986082383866,&{}w_{15} = -0.000245284111217, \\ w_{16} = 0.000137223973872 , &{} w_{17} = 0.210228581679632, &{}w_{20} = 1.0,&{} w_{21} = 0.547746158142762, \\ w_{22} = 0.127882876390368 ,&{} w_{23} = -0.011206034972369, &{} w_{24} = 0.000660308249256, &{} w_{25} = 0.001115949397675 \\ w_{26} = -0.000161611421203, &{} w_{27} = 0.210270682891451. &{}&{} \end{array}$$

5. SSP 4DGLM6-3

$$\begin{array}{llll} a^{\{1\}}_{21} = 0.374778451641205, &{} a^{\{2\}}_{21} = 0.063406760818824, &{} a^{\{3\}}_{21} = 0.008463987299019, &{} a^{\{4\}}_{21} = 0.000850022276759,\\ a^{\{1\}}_{31} = 0.357597546030056, &{} a^{\{2\}}_{31} = 0.062908428776938, &{} a^{\{3\}}_{31} = 0.008164853981020, &{} a^{\{4\}}_{31} = 0.000653850758305,\\ a^{\{1\}}_{32} = 0.325477000217070, &{} a^{\{2\}}_{32} = 0.046441087898065, &{} a^{\{3\}}_{32} = 0.005297221144835, &{} a^{\{4\}}_{32} = 0.000532701706906,\\ b^{\{1\}}_{11} = 0.334959394295523, &{} b^{\{1\}}_{12} = 0.315171444182360, &{} b^{\{1\}}_{13} = 0.410190435750393, &{} b^{\{1\}}_{21} = 0.349958069221630,\\ b^{\{1\}}_{22} = 0.292876373365019, &{} b^{\{1\}}_{23} = 0.258165929344463, &{} b^{\{2\}}_{11} = 0.060633404000675, &{} b^{\{2\}}_{12} = 0.041104145868688,\\ b^{\{2\}}_{13} = 0.041008760892016, &{} b^{\{2\}}_{21} = 0.055477164332920, &{} b^{\{2\}}_{22} = 0.047166235937992, &{} b^{\{2\}}_{23} = 0.051817450556552,\\ b^{\{3\}}_{11} = 0.007643277336581, &{} b^{\{3\}}_{12} = 0.004674306560848, &{} b^{\{3\}}_{13} = 0.005497486923106, &{} b^{\{3\}}_{21} = 0.007256291024332,\\ b^{\{3\}}_{22} = 0.005093765887795, &{} b^{\{3\}}_{23} = 0.006947776401714, &{} b^{\{4\}}_{11} = 0.000621015210638, &{} b^{\{4\}}_{12} = 0.000470045478575,\\ b^{\{4\}}_{13} = 0.000552841163009, &{} b^{\{4\}}_{21} = 0.000622129834196, &{} b^{\{4\}}_{22} = 0.000341706070841, &{} b^{\{4\}}_{23} = 0.000698685934132,\\ u_{11} = 0.630474771711679, &{} u_{12} = 0.369525228288321, &{} u_{21} = 0.573012085130541, &{} u_{22} = 0.426987914869459, \\ u_{31} = 0.601083078559332, &{} u_{32} = 0.398916921440668,&{} v = 0.378614942286516, &{} c_1 = 0.321608164825949, \\ c_2 = 0.687231609392625, &{} w_{10}= 1.0, &{} w_{11} = 0.380481257618408, &{}w_{12} = 0.048570228152514, \end{array}$$
$$\begin{array}{llll} w_{13} = 0.003531837263071, &{} w_{14} = 0.000965597584732&{} w_{15} = -0.000093904905574,&{}w_{16} = 0.837871652069336,\\ w_{20} = 1.0,&{} w_{21} = 0.221160355321244, &{} w_{22} = 0.057082983028313,&{} w_{23} = 0.008977334456590, \\ w_{24} = -0.000441185296213,&{} w_{25} = 0.000237808975927,&{} w_{26} = 0.837823139921717.&{} \end{array}$$

6. SSP 4DGLM7-3

$$\begin{array}{llll} a^{\{1\}}_{21} = 0.350457763059077, &{} a^{\{2\}}_{21} = 0.059030590724736, &{} a^{\{3\}}_{21} = 0.006167354392834, &{} a^{\{4\}}_{21} = 0.000820001027662,\\ a^{\{1\}}_{31} = 0.387500300301159, &{} a^{\{2\}}_{31} = 0.084838889640679, &{} a^{\{3\}}_{31} = 0.012031303235926, &{} a^{\{4\}}_{31} = 0.000492349845276,\\ a^{\{1\}}_{32} = 0.312881241973284, &{} a^{\{2\}}_{32} = 0.056243073304936, &{} a^{\{3\}}_{32} = 0.009017317429851, &{} a^{\{4\}}_{32} = 0.001125124849635,\\ b^{\{1\}}_{11} = 0.369607055094061, &{} b^{\{1\}}_{12} = 0.403154224734759, &{} b^{\{1\}}_{13} = 0.127967119709400, &{} b^{\{1\}}_{21} = 0.390879999306208,\\ b^{\{1\}}_{22} = 0.239443987884715 , &{} b^{\{1\}}_{23} = 0.494290470310205, &{} b^{\{2\}}_{11} = 0.058565784856034, &{} b^{\{2\}}_{12} = 0.104280749110758,\\ b^{\{2\}}_{13} = 0.008303419949253, &{} b^{\{2\}}_{21} = 0.087915116062722 , &{} b^{\{2\}}_{22} = 0.058148914188203, &{} b^{\{2\}}_{23} = 0.049797213094552,\\ b^{\{3\}}_{11} = 0.006572057700620, &{} b^{\{3\}}_{12} = 0.018705647077826, &{} b^{\{3\}}_{13} = 0.001466993217758, &{} b^{\{3\}}_{21} = 0.012839897311860,\\ b^{\{3\}}_{22} = 0.006947653665000, &{} b^{\{3\}}_{23} = 0.008829144278492, &{} b^{\{4\}}_{11} = 0.000610929864500, &{} b^{\{4\}}_{12} = 0.002527896988956,\\ b^{\{4\}}_{13} = 0.000199724984841, &{} b^{\{4\}}_{21} = 0.000420835098031, &{} b^{\{4\}}_{22} = 0.000858837048376, &{} b^{\{4\}}_{23} = 0.001202326356901,\\ u_{11} = 0.558164113618959, &{} u_{12} = 0.441835886381041, &{} u_{21} = 0.589995146907839, &{} u_{22} = 0.410004853092161, \\ u_{31} = 0.537204663265761, &{} u_{32} = 0.462795336734239, &{} v = 0.443402333155673, &{} c_1 = 0.294925929008912, \\ c_2 = 0.638257167504055, &{} w_{10}= 1.0, &{} w_{11} = 0.196005034140514, &{} w_{12} = 0.013033449258411,\\ w_{13} = 0.007614583616032, &{} w_{14} = -0.001144243875588,&{} w_{15} = -0.000104282181364, &{} w_{16} = 0.000081762590702,\\ w_{17} = 0.749648748323158, &{} w_{20} = 1.0, &{}w_{21} = 0.419891092103421, &{} w_{22} = 0.081966742096937,\\ w_{23} = 0.000057305547194,&{} w_{24} = 0.002158981114169, &{} w_{25} = 0.000173822525851,&{} w_{26} = -0.000101220718724,\\ w_{27} = 0.749692058749461.&{}&{}&{} \end{array}$$

7. SSP 4DGLM8-3

$$\begin{array}{llll} a^{\{1\}}_{21} = 0.175790178224457, &{} a^{\{2\}}_{21} = 0.053976619001249, &{} a^{\{3\}}_{21} = 0.014560267078991, &{} a^{\{4\}}_{21} = 0.002914857159230,\\ a^{\{1\}}_{31} = 0.193854979888018, &{} a^{\{2\}}_{31} = 0.027727867380224, &{} a^{\{3\}}_{31} = 0.005382677196853, &{} a^{\{4\}}_{31} = 0.001097886442691,\\ a^{\{1\}}_{32} = 0.344954266207200, &{} a^{\{2\}}_{32} = 0.013247065452726, &{} a^{\{3\}}_{32} = 0.001182532004156, &{} a^{\{4\}}_{32} = 0.000163946507126,\\ b^{\{1\}}_{11} = 0.350470082796973, &{} b^{\{1\}}_{12} = 0.207739507894165, &{} b^{\{1\}}_{13} = 0.323978091749971, &{} b^{\{1\}}_{21} = 0.336851998589390,\\ b^{\{1\}}_{22} = 0.379664713420180, &{} b^{\{1\}}_{23} = 0.475765720663504, &{} b^{\{2\}}_{11} = 0.055651506187291, &{} b^{\{2\}}_{12} = 0.102852985251848,\\ b^{\{2\}}_{13} = 0.027042199636409, &{} b^{\{2\}}_{21} = 0.114564248168959, &{} b^{\{2\}}_{22} = 0.121907339183384, &{} b^{\{2\}}_{23} = 0.134966509007059,\\ b^{\{3\}}_{11} = 0.005747532077953, &{} b^{\{3\}}_{12} = 0.007546452267841, &{} b^{\{3\}}_{13} = 0.007094916636282, &{} b^{\{3\}}_{21} = 0.030041698640272,\\ b^{\{3\}}_{22} = 0.027573371342666, &{} b^{\{3\}}_{23} = 0.038269689121708, &{} b^{\{4\}}_{11} = 0.001039724633659, &{} b^{\{4\}}_{12} = 0.000079054390091,\\ b^{\{4\}}_{13} = 0.001572203392119, &{} b^{\{4\}}_{21} = 0.003491131979020, &{} b^{\{4\}}_{22} = 0.006063710347766, &{} b^{\{4\}}_{23} = 0.002985797295388,\\ u_{11} = 0.991567328795643, &{} u_{12} = 0.008432671204357, &{} u_{21} = 0.184632179631794 , &{} u_{22} = 0.815367820368206, \\ u_{31} = 0.678379155693658, &{} u_{32} = 0.321620844306342,&{} v = 0.379923611962994, &{} c_1 = 0.364072745591117, \\ c_2 = 0.790089277348930, &{} w_{10}= 1.0, &{} w_{11} = 0.361457818520213, &{} w_{12} = 0.064938219272829, \\ w_{13} = 0.007747210371254, &{} w_{14} = 0.000708041762913,&{} w_{15} = 0.000054105005786, &{} w_{16} = 0.000003491031849,\\ w_{17} = 0.000000163872239, &{} w_{18} = 0.982635662271492, &{} w_{20} = 1.0,&{}w_{21} = 0.671552568752178 ,\\ w_{22} = 0.223400791323222, &{} w_{23} = 0.042813264929839, &{} w_{24} = 0.003555229580558, &{} w_{25} = -0.000040886308458,\\ w_{26} = -0.000026939548375,&{} w_{27} = 0.000000679871749, &{} w_{28} = 0.982637254619139. &{} \end{array}$$

8. SSP 4DGLM9-3

$$\begin{array}{llll} a^{\{1\}}_{21} = 0.568808081207977, &{} a^{\{2\}}_{21} = 0.048114396995161, &{} a^{\{3\}}_{21} = 0.010788380615035, &{} a^{\{4\}}_{21} = 0.006008124562918,\\ a^{\{1\}}_{31} = 0.344187432821678, &{} a^{\{2\}}_{31} = 0.042382496857406, &{} a^{\{3\}}_{31} = 0.003582825049991, &{} a^{\{4\}}_{31} = 0.000689205385252,\\ a^{\{1\}}_{32} = 0.340398899955966, &{} a^{\{2\}}_{32} = 0.014335262109803, &{} a^{\{3\}}_{32} = 0.000313906335632, &{} a^{\{4\}}_{32} = 0.000145276246639,\\ b^{\{1\}}_{11} = 0.982954717825614, &{} b^{\{1\}}_{12} = 0.014490770169346, &{} b^{\{1\}}_{13} = 0.013584892713300, &{} b^{\{1\}}_{21} = 0.443809258398672,\\ b^{\{1\}}_{22} = 0.135975551664887, &{} b^{\{1\}}_{23} = 0.118857631207925, &{} b^{\{2\}}_{11} = 0.212259343381131, &{} b^{\{2\}}_{12} = 0.273158542191652,\\ b^{\{2\}}_{13} = 0.002916848832074, &{} b^{\{2\}}_{21} = 0.142520928035879, &{} b^{\{2\}}_{22} = 0.136853198913849, &{} b^{\{2\}}_{23} = 0.018625818520990,\\ b^{\{3\}}_{11} = 0.018327446754578, &{} b^{\{3\}}_{12} = 0.002170604033030, &{} b^{\{3\}}_{13} = 0.002168545523328, &{} b^{\{3\}}_{21} = 0.056096865472845,\\ b^{\{3\}}_{22} = 0.096389327446308, &{} b^{\{3\}}_{23} = 0.012468767290534, &{} b^{\{4\}}_{11} = 0.000413806824034, &{} b^{\{4\}}_{12} = 0.000000761021627,\\ b^{\{4\}}_{13} = 0.001208578960785, &{} b^{\{4\}}_{21} = 0.006136911418370, &{} b^{\{4\}}_{22} = 0.033053608345553, &{} b^{\{4\}}_{23} = 0.004291265251185,\\ u_{11} = 0.957045804986185, &{} u_{12} = 0.042954195013815, &{} u_{21} = 0.684034016720173, &{} u_{22} = 0.315965983279827, \\ u_{31} = 0.929009329287935, &{} u_{32} = 0.070990670712065,&{} v = 0.035309880170621, &{} c_1 = 0.324171924094799, \\ c_2 = 0.807694415324405, &{} w_{10}= 1.0, &{} w_{11} = 0.337590296565330, &{} w_{12} = 0.046071695897029,\\ w_{13} = 0.001607713367915, &{} w_{14} = 0.000143963069728,&{} w_{15} = 0.000063618469522, &{}w_{16} = 0.000006654666131,\\ w_{17} = -0.000000395816761, &{} w_{18} = -0.000000198789037, &{} w_{19} = 0.986560378780447,&{}w_{20} = 1.0,\\ w_{21} = 0.025202357128554, &{} w_{22} = 0.196744343505741,&{} w_{23} = 0.096360260165478, &{} w_{24} = 0.007504764895165,\\ w_{25} = -0.000722929866516,&{} w_{26} = -0.000110745594193,&{} w_{27} = 0.000010556807649,&{} w_{28} = 0.000004499558562,\\ w_{29} = 0.986558896598726. &{}&{}&{} \end{array}$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Moradi, A., Chouchoulis, J., D’Ambrosio, R. et al. Jacobian-free explicit multiderivative general linear methods for hyperbolic conservation laws. Numer Algor 97, 1823–1858 (2024). https://doi.org/10.1007/s11075-024-01771-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-024-01771-6

Keywords

Mathematics Subject Classification (2010)