High-order $L^{2}$-bound-preserving Fourier pseudo-spectral schemes for the Allen-Cahn equation

Abstract

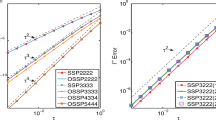
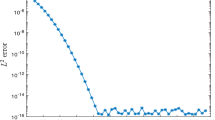
In this paper, we present a class of high-order, large time-stepping, and delay-free stabilization schemes for the Allen-Cahn equation. First, we apply a Fourier pseudo-spectral method for spatial discretization, and then, we establish the $l^{2}$-bound of the semi-discrete system. Furthermore, by adopting a time-step-dependent stabilization technique and taking advantage of recursive approximation of the exponential functions, we propose a class of stabilization Runge-Kutta schemes that preserve $l^2$-bound for any time-step size. Finally, we eliminate the delayed convergence brought by stabilization via a relaxation technique. Consequently, the resulting up-to-fourth-order parametric relaxation integrating factor Runge-Kutta (pRIFRK) schemes preserve the $l^{2}$-boundedness unconditionally with suitably chosen stabilization parameters. We also prove that the first-order pRIFRK scheme is unconditionally dissipative, w.r.t. a modified energy function, and the temporal convergence in the $l^{2}$-norm is estimated with pth-order accuracy. Numerical experiments are carried out to demonstrate the high-order accuracy, structure-preserving properties, and performance of the proposed schemes.

Appendices

Appendix A. Some non-negative RK Butcher tableaux with non-decreasing abscissas and optimal SSP coefficients

(46)

RK$^+$(5, 4) [13], $\mathcal {C} = 1.346586417284006$, $c \approx [0, 0.4549, 0.5165, 0.5165, 0.9903]^T$:

$$\begin{aligned} \left\{ \begin{aligned} u_{n, 1}&= 0.387392167970373 u_{n, 0} + 0.612607832029627[ u_{n, 0} + \frac{\tau }{\mathcal {C}} f(t_{n, 0}, u_{n, 0})], \\ u_{n, 2}&= 0.568702484115635 u_{n, 0} + 0.431297515884365[ u_{n, 1} + \frac{\tau }{\mathcal {C}} f(t_{n, 1}, u_{n, 1})], \\ u_{n, 3}&= 0.589791736452092 u_{n, 0} + 0.410208263547908[u_{n, 2} + \frac{\tau }{\mathcal {C}} f(t_{n, 2}, u_{n, 2})], \\ u_{n, 4}&= 0.213474206786188 u_{n, 0} + 0.786525793213812[u_{n, 3} + \frac{\tau }{\mathcal {C}} f(t_{n, 3}, u_{n, 3})], \\ u^{n+1}&= 0.270147144537063 u_{n, 0} + 0.029337521506634[u_{n, 0} + \frac{\tau }{\mathcal {C}} f(t_{n, 0}, u_{n, 0})] \\&\quad + 0.239419175840559[u_{n, 1} + \frac{\tau }{\mathcal {C}} f(t_{n, 1}, u_{n, 1})]\\&\quad + 0.227000995504038[ u_{n, 3} + \frac{\tau }{\mathcal {C}} f(t_{n, 3}, u_{n, 3})] \\&\quad + 0.234095162611706[u_{n, 4} + \frac{\tau }{\mathcal {C}} f(t_{n, 4}, u_{n, 4})]. \end{aligned} \right. \end{aligned}$$

(47)

Appendix B. Butcher tableaux of ETDRK schemes

Some first- and second-order ETDRK schemes that preserve $l^{2}$-boundedness are presented in the following Butcher-like tableaux.

(48)

Among them, the abscissas of ETDEKII and ETDRKIV schemes are required to meet $c_{1} \ge 1$, the abscissa of ETDRKIII scheme is required to meet $c_{1} \ge \frac{1}{2}$, and $\varphi _{k, i}\left( \tau L_{\kappa }\right) =\varphi _{k}\left( c_{i} \tau L_{\kappa }\right)$.

Appendix C. Error estimates with global Lipschitz assumption

We modify the potential function F(u) such that its second derivative is bounded. For a large enough constant $\beta > 1$, we modify F(u) by

$$\begin{aligned} \tilde{F}(u)=\left\{ \begin{array}{ll} \frac{3 \beta ^{2}-1}{2} u^{2}-2 \beta ^{3} u+\frac{1}{4}\left( 3 \beta ^{4}+1\right) , &{} u>\beta , \\ \frac{1}{4}\left( u^{2}-1\right) ^{2}, &{} u \in \left[ -\beta , \beta \right] , \\ \frac{3 \beta ^{2}-1}{2} u^{2}+2 \beta ^{3} u+\frac{1}{4}\left( 3 \beta ^{4}+1\right) , &{} u<-\beta . \end{array}\right. \end{aligned}$$

Then we replace f(u) by,

$$\begin{aligned} \tilde{f}(u)=-\tilde{F}^{\prime }(u)=\left\{ \begin{array}{ll} -\left( 3 \beta ^{2}-1\right) u+2 \beta ^{3}, &{} u>\beta , \\ -\left( u^{2}-1\right) u, &{} u \in \left[ -\beta , \beta \right] , \\ -\left( 3 \beta ^{2}-1\right) u-2 \beta ^{3}, &{} u<-\beta . \end{array}\right. \end{aligned}$$

Thus, we have $\max _{u \in \mathbb {R}}|\tilde{f}^{\prime }(u)| \le 3 \beta ^{2}-1$.

Lemma C.1

Given any fixed $t \in (0, T]$, when $\kappa >0$, there exists $l_{\kappa }=3 \beta ^{2}-1+\kappa$, such that for all $\varvec{u}, \varvec{v} \in \mathbb {R}^{N},\Vert \varvec{u}\Vert _{l^{2}} \le 1,\Vert \varvec{v}\Vert _{l^{2}} \le 1$, we have

$$\Vert N_{\kappa }(\varvec{u})-N_{\kappa }(\varvec{v})\Vert _{l^{2}} \le l_{\kappa } \Vert \varvec{u}-\varvec{v}\Vert _{l^{2}},$$

where $l_{\kappa }$ is a constant independent of N.

Proof

It should be noted that $\Vert f^{\prime }(\varvec{u})\Vert _{l^{\infty }} \le 3 \beta ^{2}-1$. Applying Lagrange’s mean value theorem gives

$$ \Vert N_{\kappa }(\varvec{u})-N_{\kappa }(\varvec{v})\Vert _{l^{2}} \le \Vert f^{\prime }(\varvec{\xi })\Vert _{l^{\infty }}\Vert (\varvec{u}-\varvec{v})\Vert _{l^{2}}+\kappa \Vert \varvec{u}-\varvec{v}\Vert _{l^{2}} \le l_\kappa \Vert \varvec{u}-\varvec{v}\Vert _{l^{2}}, $$

where $\varvec{\xi }=\theta \varvec{u}+(1-\theta ) \varvec{v}$, $\theta \in (0,1)$, and $l_{\kappa }=3 \beta ^{2}-1+\kappa$. $\square$

Theorem C.2

Assume $\varvec{u}(t) \in C^{p+1}([0, T]; \mathbb {U}^{N})$ is the exact solution to the semi-discrete ODE system (3), $\varvec{u}^{n}$ is a numerical solution computed by pRIFRK schemes with non-negative coefficients and non-decreasing parametric abscissas $\hat{c}_{i}$ that meet pth-order conditions in Table 2, when $\kappa \ge \max \{\frac{1}{\tilde{\tau }_{F E}}-\frac{\mathcal {C}}{\tau }, 0\}$, and $\Vert \varvec{u}^{0}\Vert _{l^{2}} \le 1$, we have error estimates

$$\begin{aligned} \left\| \varvec{u}\left( \hat{t}_{n}\right) -\varvec{u}^{n}\right\| _{l^{2}} \le C(e^{l_{\kappa } s \frac{\hat{t}_{n}}{\hat{c}_{s}}}-1) \tau ^{p}, \hat{t}_{n} \le T, \end{aligned}$$

where $\hat{t}_{n}=n \hat{\tau }$.

Proof

The Butcher form of the pRIFRK schemes is

$$\begin{aligned} \varvec{u}_{n, i}=\frac{1}{\psi _{i}(\tau \kappa )}\big (e^{\hat{c}_{i} \tau L} \varvec{u}^{n}+\tau \sum _{j=0}^{i-1} a_{i j} \psi _{j}(\tau \kappa ) e^{(\hat{c}_{i}-\hat{c}_{j}) \tau L} N_{\kappa }( \varvec{u}_{n, j})\big ), \quad i=1,2, \dots , s. \end{aligned}$$

(49)

We may as well set $U_{n, i}$, $0 \le i \le s$ as reference solutions for the pRIFRK schemes, and $U_{n,0}=\varvec{u}(\hat{t}_{n})$, $U_{n,s}=\varvec{u}(\hat{t}_{n+1})$. Then we have

$$\begin{aligned}&U_{n, i}=\frac{1}{\psi _{i}(\tau \kappa )}\big (e^{\hat{c}_{i} \tau L} \varvec{u}(\hat{t}_{n})+\tau \sum _{j=0}^{i-1} a_{i j} \psi _{j}(\tau \kappa ) e^{(\hat{c}_{i}-\hat{c}_{j}) \tau L} N_{\kappa }( U_{n, j})\big ), \nonumber \\&i=1,2, \dots , s-1.\end{aligned}$$

(50)

$$\begin{aligned}&U_{n, s}=\frac{1}{\psi _{s}(\tau \kappa )}\big (e^{\hat{c}_{s} \tau L} \varvec{u}(\hat{t}_{n})+\tau \sum _{j=0}^{s-1} a_{s j} \psi _{j}(\tau \kappa ) e^{(\hat{c}_{s}-\hat{c}_{j}) \tau L} N_{\kappa }( U_{n, j})\big )+R_{s}^{n} . \end{aligned}$$

(51)

According to Theorem 3.2, for an s-stage pth-order pRIFRK scheme, the truncation error of pRIFRK solution satisfies

$$\begin{aligned} \max _{0 \le n \le \left[ \frac{T}{\hat{\tau }}\right] -1}\left\| R_{s}^{n}\right\| _{l^{2}} \le C_{s} \tau ^{p+1}, \end{aligned}$$

(52)

where $C_{s}$ depends on the $C^{p+1}[0, T]$-norm of $\varvec{u}$, $\Vert L\Vert _{\infty }$, N, s, and $\kappa$, but is independent of $\tau$. Assume $e^{n}=\varvec{u}(\hat{t}_{n})-\varvec{u}^{n}$, $e_{n, i}=U_{n, i}-\varvec{u}_{n, i}$, $1 \le i \le s$. Then $e_{n, 0}=e^{n}, e_{n, s}=e^{n+1}$. Let $\varDelta _{n, j}=N_{\kappa }( U_{n, j})-N_{\kappa }(\varvec{u}_{n, j})$, subtract (49) from (50) and (51), and we can obtain

$$\begin{aligned}&e_{n, i}=\frac{1}{\psi _{i}(\tau \kappa )}\big (e^{\hat{c}_{i} \tau L} e^{n}+\tau \sum _{j=0}^{i-1} a_{i j} \psi _{j}(\tau \kappa ) e^{(\hat{c}_{i}-\hat{c}_{j}) \tau L} \varDelta _{n, j}\big ), \quad i=1,2, \dots , s-1.\end{aligned}$$

(53)

$$\begin{aligned}&e^{n+1}=\frac{1}{\psi _{s}(\tau \kappa )}\big (e^{\hat{c}_{s} \tau L} e^{n}+\tau \sum _{j=0}^{s-1} a_{s j} \psi _{j}(\tau \kappa ) e^{(\hat{c}_{s}-\hat{c}_{j}) \tau L} \varDelta _{n, j}\big )+R_{s}^{n}. \end{aligned}$$

(54)

According to Lemmas 2.3, C.1, using the triangle inequality, we can obtain

$$\begin{aligned} \begin{aligned} \Vert e_{n, i}\Vert _{l^{2}}&\le \frac{1}{\psi _{i}(\tau \kappa )}[\Vert e^{\hat{c}_{i} \tau L} e^{n}\Vert _{l^{2}}+\tau \sum _{j=0}^{i-1} a_{i j} \psi _{j}(\tau \kappa )\Vert e^{(\hat{c}_{i}-\hat{c}_{j}) \tau L} \varDelta _{n, j}\Vert _{l^{2}}] \\&\le \frac{1}{\psi _{i}(\tau \kappa )}[\Vert e^{n}\Vert _{l^{2}}+\tau \sum _{j=0}^{i-1} a_{i j} \psi _{j}(\tau \kappa )\Vert \varDelta _{n, j}\Vert _{l^{2}}] \\&\le [\Vert e^{n}\Vert _{l^{2}}+\tau l_{\kappa } \sum _{j=0}^{i-1}\Vert e_{n, j}\Vert _{l^{2}}] \\&\le (1+l_{\kappa } \tau )^{i}\Vert e^{n}\Vert _{l^{2}},\quad i=1, \dots , s-1. \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} \Vert e_{n, s}\Vert _{l^{2}}&\le \frac{1}{\psi _{s}(\tau \kappa )}[\Vert e^{\hat{c}_{s} \tau L} e^{n}\Vert _{l^{2}}+\tau \sum _{j=0}^{s-1} a_{s j} \psi _{j}(\tau \kappa )\Vert e^{(\hat{c}_{s}-\hat{c}_{j}) \tau L} \varDelta _{n, j}\Vert _{l^{2}}]+\Vert R_{s}^{n}\Vert _{l^{2}} \\&\le \Vert e^{n}\Vert _{l^{2}}+\tau l_{\kappa } \sum _{j=0}^{s-1}\Vert e_{n, j}\Vert _{l^{2}}+\Vert R_{s}^{n}\Vert _{l^{2}} \\&\le (1+l_{\kappa } \tau )^{s}\Vert e^{n}\Vert _{l^{2}}+C_{s} \tau ^{p+1}. \end{aligned} \end{aligned}$$

Then we have

$$\begin{aligned} \begin{aligned} \Vert e^{n+1}\Vert _{l^{2}}&\le (1+l_{\kappa } \tau )^{s}\Vert e^{n}\Vert _{l^{2}}+C_{s} \tau ^{p+1} \\&\le (1+l_{\kappa } \tau )^{s(n+1)}\Vert e^{0}\Vert _{l^{2}}+C_{s} \tau ^{p+1} \sum _{i=0}^{n}(1+l_{\kappa } \tau )^{s i} \\&\le (1+l_{\kappa } \tau )^{s(n+1)}\Vert e^{0}\Vert _{l^{2}}+\frac{C_{s}}{l_{\kappa } s}(e^{l_{\kappa } s(n+1) \tau }-1) \tau ^{p}, \end{aligned} \end{aligned}$$

i.e.,

$$\begin{aligned} \Vert e^{n}\Vert _{l^{2}} \le (1+l_{\kappa } \tau )^{s n}\Vert e^{0}\Vert _{l^{2}}+\frac{C_{s}}{l_{\kappa } s}(e^{l_{\kappa } s n \tau }-1) \tau ^{p}. \end{aligned}$$

Assume $\Vert e^{0}\Vert =0$, $n \tau =\frac{\hat{t}_{n}}{\hat{c}_{s}}$, $C=\frac{C_{s}}{l_{\kappa } s}$. Then we can obtain $\Vert e^{n}\Vert _{l^{2}} \le C(e^{l_{\kappa } s \frac{\hat{t}_{n}}{\hat{c}_{s}}}-1) \tau ^{p}.$ $\square$