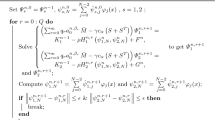Skip to main content
Springer Nature Link
Log in

Novel numerical methods based on graded, adaptive and uniform meshes for a time-fractional advection-diffusion equation subjected to weakly singular solution

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

This paper presents adaptive, graded and uniform mesh schemes to approximate the solution of a fractional order advection-diffusion model, which generally shows a weak singularity at the initial time level. The temporal fractional derivative in the underlying problem is described in a Caputo form and is discretized by means of L1 scheme on a nonuniform mesh. The space derivative is discretized on a uniform mesh employing a fourth-order compact finite difference scheme. The adaptive grid is generated via equidistribution of a positive monitor function. Stability and convergence results for the proposed method on graded mesh are established. Numerical examples are provided to study the accuracy and efficiency of the proposed techniques and to support the theoretical results. A discussion about the advantages of the graded and adaptive meshes over the uniform one is also presented. The CPU times for the proposed numerical schemes are provided.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Availability of supporting data

Not applicable

References

  1. Podlubny, I.: Fractional Differential equations. Academic, New York (1999)

    MATH  Google Scholar 

  2. Giona, M., Cerbelli, S., Roman, H.E.: Fractional diffusion equation and relaxation in complex viscoelastic materials. Phys. A 191, 449–453 (1992)

    MATH  Google Scholar 

  3. Mainardi, F.: Fractals and Fractional Calculus Continuum Mechanics. Springer Verlag 378, 291–348 (1997)

  4. Roul, P.: Design and analysis of efficient computational techniques for solving a temporal-fractional partial differential equation with the weakly singular solution. Math. Methods Appl. Sci. 47(4), 2226–2249 (2024)

    MathSciNet  MATH  Google Scholar 

  5. Diethelm, K., Freed, A.D.: On the solution of nonlinear fractional order differential equations used in the modelling of viscoplasticity. In: Scientific Computing in Chemical Engineering II: Computational Fluid Dynamics, Reaction Engineering and Molecular Properties, pp. 217-224. Springer Verlag, Heidelberg (1999)

  6. Bagley, R.L., Torvik, P.J.: On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 51, 294–298 (1984)

    MATH  Google Scholar 

  7. Roul, P.: A high accuracy numerical method and its convergence for time-fractional Black-Scholes equation governing European options. Appl. Numer. Math. 151, 472–493 (2020)

    MathSciNet  MATH  Google Scholar 

  8. Roul, P., Rohil, V., Espinosa-Paredes, G., Obaidurrahman, K.: An efficient computational technique for solving a fractional-order model describing dynamics of neutron flux in a nuclear reactor. Ann. Nucl. Energy 185, 109733 (2023)

    MATH  Google Scholar 

  9. Benson, D., Wheatcraft, S., Meerschaert, M.: Application of a fractional advection-dispersion equation. Water Resour. Res. 36, 1403–1412 (2000)

    MATH  Google Scholar 

  10. Dipierro, S., Valdinoci, E.: A simple mathematical model inspired by the Purkinje cells: From delayed travelling waves to fractional diffusion. Bull. Math. Biol. (2018)

  11. Diethelm, K.: The analysis of fractional differential equations. In: Lecture Notes in Mathematics. Berlin: Springer-Verlag (2010)

  12. Stynes, M., O’Riordan, E., Gracia, J.: Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 55(2), 1057–1079 (2017)

    MathSciNet  MATH  Google Scholar 

  13. Zhuang, P., Gu, Y.T., Liu, F., Turner, I., Yarlagadda, P.K.D.V.: Time-dependent fractional advection-diffusion equations by an implicit MLS meshless method. Int. J. Numer. Methods Eng. 88(13), 1346–1362 (2011)

    MathSciNet  MATH  Google Scholar 

  14. Azin, H., Mohammadi F., Heydari, M.H.: A hybrid method for solving time fractional advection-diffusion equation on unbounded space domain. Adv. Differ. Equ. 596 (2020)

  15. Li, C., Cao, J., Li, H.: High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations (III). J. Comput. Appl. Math. 299, 159–175 (2016)

    MathSciNet  MATH  Google Scholar 

  16. Cao, J., Li, C., Chen, Y.: High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations (II). Fract. Calc. Appl. Anal. 18(3), 735–761 (2015)

    MathSciNet  MATH  Google Scholar 

  17. Mardani, A., Hooshmandasl, M.R., Heydari, M.H., Cattani, C.: A meshless method for solving the time fractional advection-diffusion equation with variable coefficients. Comput. Math. Appl. 75, 122–133 (2018)

    MathSciNet  MATH  Google Scholar 

  18. Gowrisankar, S., Natesan, S.: The parameter uniform numerical method for singularly perturbed parabolic reaction-diffusion problems on equidistributed grids. Appl. Math. Lett. 26, 1053–1060 (2013)

    MathSciNet  MATH  Google Scholar 

  19. Kopteva, N., Madden, N., Stynes, M.: Grid equidistribution for reaction-diffusion problems in one dimension. Numer. Algorithms 40(3), 305–322 (2005)

    MathSciNet  MATH  Google Scholar 

  20. Chen, Y.: Uniform convergence analysis of finite difference approximations for singular perturbation problems on an adapted grid. Adv. Comput. Math. 24, 197–212 (2006)

    MathSciNet  MATH  Google Scholar 

  21. Ford, N.J., Xiao, J., Yan, Y.: A finite element method for time fractional partial differential equations. Fract. Calc. Appl. Anal. 14, 454–474 (2011)

    MathSciNet  MATH  Google Scholar 

  22. Lin, Y., Xu, C.: Finite difference/spectral approximations for the time fractional diffusion equation. J. Comput. Phys. 225, 1533–1552 (2007)

    MathSciNet  MATH  Google Scholar 

  23. Ammi, M.R.S., Jamiai, I., Torres, D.F.M.: A finite element approximation for a class of Caputo time-fractional diffusion equations. Comput. Math. Appl. 78, 1334–1344 (2019)

    MathSciNet  MATH  Google Scholar 

  24. Murio, D.A.: Implicit finite difference approximation for time fractional diffusion equations. Comput. Math. Appl. 56, 1138–1145 (2008)

    MathSciNet  MATH  Google Scholar 

  25. Sweilam, N.H., Khader, M.M., Mahdy, A.M.S.: Crank-Nicoloson finite difference method for solving time-fractional diffusion equation. J. Frac. Calc. Appl. 2, 1–9 (2012)

    MATH  Google Scholar 

  26. Du, R., Cao, R., Sun, Z.Z.: A compact difference scheme for the fractional diffusion-wave equation. Appl. Math. Model. 34, 2998–3007 (2010)

    MathSciNet  MATH  Google Scholar 

  27. Roul, P., Goura, V.M.K.P., Cavoretto, R.: A numerical technique based on B-spline for a class of time-fractional diffusion equation. Numer. Methods Partial Differ. 39(1), 45–64 (2023)

    MathSciNet  MATH  Google Scholar 

  28. Liu, Y., Du, Y., Li, H., Wang, J.: An \(H^1-\)Galerkin mixed finite element method for time fractional reaction-diffusion equation. J. Appl. Math. Comput. 47, 103–117 (2015)

    MathSciNet  MATH  Google Scholar 

  29. Zhang, J., Yang, X.: A class of efficient difference method for time fractional reaction-diffusion equation. Comp. Appl. Math. 37, 4376–4396 (2018)

    MathSciNet  MATH  Google Scholar 

  30. Gong, C., Bao, W., Tang, G., Yang, B., Liu, J.: An efficient parallel solution for Caputo fractional reaction-diffusion equation. J. Supercomput. 68, 1521–1537 (2014)

    MATH  Google Scholar 

  31. Roul, P., Goura, V.M.K.P.: A high order numerical scheme for solving a class of non-homogeneous time-fractional reaction diffusion equation. Numer. Methods Partial Differ. 37(2), 1506–1534 (2021)

    MathSciNet  MATH  Google Scholar 

  32. Das, P., Rana, S., Ramos, H.: A perturbation-based approach for solving fractional-order Volterra-Fredholm integro differential equations and its convergence analysis. Int. J. Comput. Math. 97(10), 1994–2014 (2020)

    MathSciNet  MATH  Google Scholar 

  33. Yang, X., Zhang, Z.: On conservative, positivity preserving, nonlinear FV scheme on distorted meshes for the multi-term nonlocal Nagumo-type equations. Appl. Math. Lett. 150, 108972 (2024)

    MathSciNet  MATH  Google Scholar 

  34. Zhang, H., Yang, X., Tang, Q., Xu, D.: A robust error analysis of the OSC method for a multi-term fourth-order sub-diffusion equation. Comput. Math. Appl. 109, 180–190 (2022)

    MathSciNet  MATH  Google Scholar 

  35. Wang, W., Zhang, H., Jiang, X., Yang, X.: A high-order and efficient numerical technique for the nonlocal neutron diffusion equation representing neutron transport in a nuclear reactor. Ann. Nucl. Energy 195, 110163 (2024)

    MATH  Google Scholar 

  36. Yang, X., Zhang, H.: The uniform \(l^1\) long-time behavior of time discretization for time-fractional partial differential equations with nonsmooth data. Appl. Math. Lett. 124, 107644 (2022)

    MATH  Google Scholar 

  37. Yang, X., Zhang, H., Zhang, Q., Yuan, G.: Simple positivity-preserving nonlinear finite volume scheme for subdiffusion equations on general non-conforming distorted meshes. Nonlinear Dyn. 108, 3859–3886 (2022)

    MATH  Google Scholar 

  38. Yang, X., Zhang, Q., Yuan, G., Sheng, Z.: On positivity preservation in nonlinear finite volume method for multi-term fractional subdiffusion equation on polygonal meshes. Nonlinear Dyn. 92, 595–612 (2018)

    MATH  Google Scholar 

  39. Huang, J., Cen, Z., Zhao, J.: An adaptive moving mesh method for a time-fractional Black-Scholes equation. Adv. Differ. Equ. 2019, 516 (2019)

    MathSciNet  MATH  Google Scholar 

  40. Roul, P., Rohil, V.: A novel high-order numerical scheme and its analysis of the two-dimensional time fractional reaction-subdiffusion equation. Numer. Algor. 90(4), 1357–1387 (2022)

    MathSciNet  MATH  Google Scholar 

  41. Choudhary, R., Singh, S., Das, P., Kumar, D.: A higher-order stable numerical approximation for time-fractional non-linear Kuramoto-Sivashinsky equation based on quintic B-spline. Math. Method Appl. Sci. (2023). https://doi.org/10.1002/mma.9778

    Article  MATH  Google Scholar 

  42. Roul, P., Rohil, V.: A high-order numerical scheme based on graded mesh and its analysis for the two-dimensional time-fractional convection-diffusion equation. Comput. Math. Appl. 126, 1–13 (2022)

    MathSciNet  MATH  Google Scholar 

  43. Santra, S., Mohapatra, J., Das, P., Choudhuri, D.: Higher order approximations for fractional order integro-parabolic partial differential equations on an adaptive mesh with error analysis. Comput. Math. Appl. 150, 87–101 (2023)

    MathSciNet  MATH  Google Scholar 

  44. Zhou, Z., Zhang, H., Yang, X.: \(H^1\)-norm error analysis of a robust ADI method on graded mesh for three-dimensional subdiffusion problems. Numer. Algor. (2023). https://doi.org/10.1007/s11075-023-01676-w

    Article  MATH  Google Scholar 

  45. Das, P.: An a posteriori based convergence analysis for a nonlinear singularly perturbed system of delay differential equations on an adaptive mesh. Numer. Algor. 81, 465–487 (2019)

    MathSciNet  MATH  Google Scholar 

  46. Das, P.: Comparison of a priori and a posteriori meshes for singularly perturbed nonlinear parameterized problems. J. Comput. Appl. Math. 290, 16–25 (2015)

    MathSciNet  MATH  Google Scholar 

  47. Roul, P., Rohil, V.: An efficient numerical scheme and its analysis for the multiterm time-fractional convection-diffusion-reaction equation. Math. Method Appl. Sci. 46(16), 16857–16875 (2023)

    MathSciNet  MATH  Google Scholar 

  48. Das, P.: A higher order difference method for singularly perturbed parabolic partial differential equations. J. Differ. Equ. Appl. 24(3), 452–477 (2018)

    MathSciNet  MATH  Google Scholar 

  49. Das, P., Natesan, S.: Numerical solution of a system of singularly perturbed convection diffusion boundary value problems using mesh equidistribution technique. Aust. J. Math. Anal. Appl. 10(1), 1–17 (2013)

    MathSciNet  MATH  Google Scholar 

  50. Luchko, Y.: Initial-boundary-value problems for the one-dimensional time-fractional diffusion equation. Fract. Calc. Appl. Anal. 15, 141–160 (2012)

    MathSciNet  MATH  Google Scholar 

  51. Li, C., Wang, Z.: Numerical Methods for the Time Fractional Convection-Diffusion-Reaction Equation. Numer. Funct. Anal. Optim. 42(10), 1115–1153 (2021)

    MathSciNet  MATH  Google Scholar 

  52. Das, P., Rana, S., Ramos, H.: On the approximate solutions of a class of fractional order nonlinear Volterra integro-differential initial value problems and boundary value problems of first kind and their convergence analysis. J. Comput. Appl. Math. 404, 113116 (2022)

    MathSciNet  MATH  Google Scholar 

Download references

Funding

The first author received financial support from NBHM, DAE under the project no. \( 02011/7/2023/NBHM (RP)/R \& D II/ 2877\).

Author information

Authors and Affiliations

  1. Department of Mathematics, VNIT, Nagpur, MS, 440010, India

    Pradip Roul

  2. Department of Mathematics, Indian Institute of Technology Madras, Chennai, 600036, India

    S. Sundar

Authors
  1. Pradip Roul
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. S. Sundar
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Pradip Roul: conceptualization, methodology, data curation, writing—original draft, software, investigation, validation. S. Sundar: methodology, validation.

Corresponding author

Correspondence to Pradip Roul.

Ethics declarations

Ethics approval and consent to participate

Not applicable

Consent for publication

The authors give their consent for the publication of the details within the text (“Material”) to be published in the Journal and Article.

Human and animal ethics

Not applicable

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Roul, P., Sundar, S. Novel numerical methods based on graded, adaptive and uniform meshes for a time-fractional advection-diffusion equation subjected to weakly singular solution. Numer Algor 98, 531–561 (2025). https://doi.org/10.1007/s11075-024-01804-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-024-01804-0

Keywords