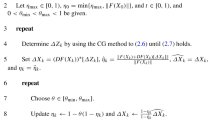Skip to main content
Springer Nature Link
Log in

An Ulm-like algorithm for generalized inverse eigenvalue problems

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

In this paper, we study the numerical solutions of the generalized inverse eigenvalue problem (for short, GIEP). Motivated by Ulm’s method for solving general nonlinear equations and the algorithm of Aishima (J. Comput. Appl. Math. 367, 112485 2020) for the GIEP, we propose here an Ulm-like algorithm for the GIEP. Compared with other existing methods for the GIEP, the proposed algorithm avoids solving the (approximate) Jacobian equations and so it seems more stable. Assuming that the relative generalized Jacobian matrices at a solution are nonsingular, we prove the quadratic convergence property of the proposed algorithm. Incidentally, we extend the work of Luo et al. (J. Nonlinear Convex Anal. 24, 2309–2328 2023) for the inverse eigenvalue problem (for short, IEP) to the GIEP. Some numerical examples are provided and comparisons with other algorithms are made.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Algorithm 1
Algorithm 2
Fig. 1

Similar content being viewed by others

Data Availability

No datasets were generated or analysed during the current study.

Code Availability

Not applicable.

References

  1. Aishima, K.: A quadratically convergent algorithm based on matrix equations for inverse eigenvalue problems. Linear Algebra Appl. 542, 310–333 (2018)

    MathSciNet  MATH  Google Scholar 

  2. Aishima, K.: A quadratically convergent algorithm for inverse eigenvalue problems with multiple eigenvalues. Linear Algebra Appl. 549, 30–52 (2018)

    MathSciNet  MATH  Google Scholar 

  3. Aishima, K.: A quadratically convergent algorithm for inverse generalized eigenvalue problems. J. Comput. Appl. Math. 367, 112485 (2020)

    MathSciNet  MATH  Google Scholar 

  4. Arela-Pérez, S., Lozano, C., Nina, H., Pickmann-Soto, H., Rodríguez, J.: The new inverse eigenvalue problems for periodic and generalized periodic Jacobi matrices from their extremal spectral data. Linear Algebra Appl. 659, 55–72 (2023)

    MathSciNet  MATH  Google Scholar 

  5. Bai, Z.J., Chan, R.H., Morini, B.: An inexact Cayley transform method for inverse eigenvalue problems. Inverse Probl. 20, 1675–1689 (2004)

    MathSciNet  MATH  Google Scholar 

  6. Bai, Z.J., Jin, X.Q.: A note on the Ulm-like method for inverse eigenvalue problems. Recent Advances in Scientific Computing and Matrix Analysis, 1–7 (2011)

  7. Behera, K.K.: A generalized inverse eigenvalue problem and m-functions. Linear Algebra Appl. 622, 46–65 (2021)

    MathSciNet  MATH  Google Scholar 

  8. Cai, J., Chen, J.: Iterative solutions of generalized inverse eigenvalue problem for partially bisymmetric matrices. Linear Multilinear A. 65, 1643–1654 (2017)

    MathSciNet  MATH  Google Scholar 

  9. Chan, R.H., Chung, H.L., Xu, S.F.: The inexact Newton-like method for inverse eigenvalue problem. BIT Numer. Math. 43, 7–20 (2003)

    MathSciNet  MATH  Google Scholar 

  10. Chu, M.T., Golub, G.H.: Structured inverse eigenvalue problems. Acta Numer. 11, 1–71 (2002)

    MathSciNet  MATH  Google Scholar 

  11. Dai, H.: An algorithm for symmetric generalized inverse eigenvalue problems. Linear Algebra Appl. 296, 79–98 (1999)

    MathSciNet  MATH  Google Scholar 

  12. Dai, H., Lancaster, P.: Newton’s method for a generalized inverse eigenvalue problem. Numer. Linear Algebra Appl. 4, 1–21 (1997)

    MathSciNet  MATH  Google Scholar 

  13. Dai, H., Bai, Z.Z., Wei, Y.: On the solvability condition and numerical algorithm for the parameterized generalized inverse eigenvalue problem. SIAM J. Matrix Anal. Appl. 36, 707–726 (2015)

    MathSciNet  MATH  Google Scholar 

  14. Dalvand, Z., Hajarian, M.: Newton-like and inexact Newton-like methods for a parameterized generalized inverse eigenvalue problem. Math. Methods Appl. Sci. 44, 4217–4234 (2021)

    MathSciNet  MATH  Google Scholar 

  15. Dalvand, Z., Hajarian, M., Roman, J.E.: An extension of the Cayley transform method for a parameterized generalized inverse eigenvalue problem. Numer. Linear Algebra Appl. 27, e2327 (2020)

    MathSciNet  MATH  Google Scholar 

  16. Ezquerro, J.A., Hernández, M.A.: The Ulm method under mild differentiability conditions. Numer. Math. 109, 193–207 (2008)

    MathSciNet  MATH  Google Scholar 

  17. Friedland, S., Nocedal, J., Overton, M.L.: The formulation and analysis of numerical methods for inverse eigenvalue problems. SIAM J. Numer. Anal. 24, 634–667 (1987)

    MathSciNet  MATH  Google Scholar 

  18. Gajewski, A., Zyczkowski, M.: Optimal structural design under stability constraints. Kluwer Academic, Dordrecht, The Natherlands (1988)

    MATH  Google Scholar 

  19. Galperin, A., Waksman, Z.: Ulm’s method under regular smoothness. Numer. Funct. Anal. Optim. 19, 285–307 (1998)

    MathSciNet  MATH  Google Scholar 

  20. Ghanbari, K.: A survey on inverse and generalized inverse eigenvalue problems for Jacobi matrices. Appl. Math. Comput. 195, 355–363 (2008)

    MathSciNet  MATH  Google Scholar 

  21. Ghanbari, K.: m-functions and inverse generalized eigenvalue problem. Inverse Probl. 17, 211 (2001)

    MathSciNet  MATH  Google Scholar 

  22. Golub, G.H., Van Loan, C.F.: Matrix Computations, 3rd edn. Johns Hopkins University Press, Baltimore (1996)

    MATH  Google Scholar 

  23. Grandhi, R.: Structural optimization with frequency constraints-Areview. AIAA J. 31, 2296–2303 (1993)

    MATH  Google Scholar 

  24. Gutiérrez, J.M., Hernández, M.A., Romero, N.: A note on a modification of Moser’s method. J. Complex. 24, 185–197 (2008)

    MathSciNet  MATH  Google Scholar 

  25. Hald, O.: On discrete and numerical Sturm-Liouville problems. New York University, New York (1972)

    MATH  Google Scholar 

  26. Hald, O.: On a Newton-Moser type method. Numer. Math. 23, 411–426 (1975)

    MathSciNet  MATH  Google Scholar 

  27. Harman, H.: Modern factor analysis. University of Chicago Press, Chicago (1976)

    MATH  Google Scholar 

  28. Joseph, K.T.: Inverse eigenvalue problem in structural design. AIAA J. 30, 2890–2896 (1992)

    MATH  Google Scholar 

  29. Li, R.C.: A perturbation bound for definite pencils. Linear Algebra Appl. 179, 191–202 (1993)

    MathSciNet  MATH  Google Scholar 

  30. Luo, Y.S., Shen, W.P., Luo, E.P.: A quadratically convergent algorithm for inverse eigenvalue problems. J. Nonlinear Convex Anal. 24, 2309–2328 (2023)

    MathSciNet  MATH  Google Scholar 

  31. Ma, W.: Two-step Ulm-Chebyshev-like Cayley transform method for inverse eigenvalue problems. Int. J. of Comput. Math. 99, 391–406 (2022)

    MathSciNet  MATH  Google Scholar 

  32. Shen, W.P., Li, C., Jin, X.Q.: A Ulm-like method for inverse eigenvalue problems. Appl. Numer. Math. 61, 356–367 (2011)

    MathSciNet  MATH  Google Scholar 

  33. Shen, W.P., Li, C., Jin, X.Q.: An inexact Cayley transform method for inverse eigenvalue problems with multiple eigenvalues. Inverse Probl. 31, 085007 (2015)

    MathSciNet  MATH  Google Scholar 

  34. Shen, W.P., Li, C., Jin, X.Q.: An Ulm-like Cayley transform method for inverse eigenvalue problems with multiple eigenvalues. Numer. Math. -Theory Me. 9, 664–685 (2016)

    MathSciNet  MATH  Google Scholar 

  35. Sivan, D.D., Ram, Y.M.: Mass and stiffness modifications to achieve desired natural frequencies. Commun. Numer. Methods Engrg. 12, 531–542 (1996)

    MATH  Google Scholar 

  36. Sun, D., Sun, J.: Strong semismoothness of eigenvalues of symmetric matrices and its application to inverse eigenvalue problems. SIAM J. Numer. Anal. 40, 2352–2367 (2002)

    MathSciNet  MATH  Google Scholar 

  37. Sun, J.G.: Multiple eigenvalue sensitivity analysis. Linear Algebra Appl. 137, 183–211 (1990)

    MathSciNet  MATH  Google Scholar 

  38. Ulm, S.: On iterative methods with successive approximation of the inverse operator. Izv. Akad. Nauk Est. SSR 16, 403–411 (1967)

    MATH  Google Scholar 

  39. Wen, C.T., Chen, X.S., Sun, H.W.: A two-step inexact Newton-Chebyshev-like method for inverse eigenvalue problems. Linear Algebra Appl. 585, 241–262 (2020)

    MathSciNet  MATH  Google Scholar 

  40. Xie, H.Q., Dai, H.: Inverse eigenvalue problem in structural dynamics design. Number. Math. J. Chinese Univ. 15, 97–106 (2006)

    MathSciNet  MATH  Google Scholar 

  41. Zehnder, E.J.: A remark about Newton’s method, Commun. Pure. Appl. Math. 27, 361–366 (1974)

    MathSciNet  MATH  Google Scholar 

  42. Zhang, H., Yuan, Y.: Generalized inverse eigenvalue problems for Hermitian and J-Hamiltonian/skew-Hamiltonian matrices. Appl. Math. Comput. 361, 609–616 (2019)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We would like to thank the anonymous referees for their helpful and valuable comments which lead to the improvement of this paper.

Funding

This work was supported in part by the National Natural Science Foundation of China (grant 12071441).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Zhejiang Normal University, Jinhua, 321004, People’s Republic of China

    Yusong Luo & Weiping Shen

Authors
  1. Yusong Luo
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Weiping Shen
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Yusong Luo and Weiping Shen wrote the main manuscript text. Both authors reviewed the manuscript.

Corresponding author

Correspondence to Weiping Shen.

Ethics declarations

Competing interests

The authors declare no competing interests.

Ethics approval

Not applicable.

Consent to participate

All authors participated.

Consent for publication

All authors agreed to publish.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Luo, Y., Shen, W. An Ulm-like algorithm for generalized inverse eigenvalue problems. Numer Algor 98, 1611–1641 (2025). https://doi.org/10.1007/s11075-024-01845-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-024-01845-5

Keywords

Mathematics Subject Classification (2010)