Abstract
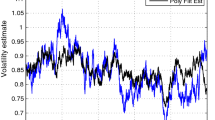
We propose an adaptive algorithm for tracking historical volatility. The algorithm borrows ideas from nonparametric statistics. In particular, we assume that the volatility is a several times differentiable function with a bounded highest derivative. We propose an adaptive algorithm with a Kalman filter structure, which guarantees the same asymptotics (well known from statistical inference) with respect to the sample size n, n → ∞. The tuning procedure for this filter is simpler than for a GARCH filter.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
Andersen, T., Bollerslev, T., Diebold, F.X., and Labys, P., Exchange Rate Returns Standardized by Realized Volatility Are (Nearly) Gaussian, Multinational Finance J., 2000, vol. 4, pp. 159–179.
Baillie, R.T. and Bollerslev, T., Prediction in Dynamic Models with Time-Dependent Conditional Variances, J. Econometrics, 1992, vol. 52, pp. 91–113.
Black, F., The Pricing of Commodity Contracts, J. Financial Economics, 1976, vol. 9, pp. 167–179.
Black, F. and Scholes, M., The Pricing of Options and Corporate Liabilities, J. Political Economics, 1973, vol. 81, pp. 637–659.
Bollerslev, T., Generalized Autoregressive Conditional Heteroskedasticity, J. Econometrics, 1986, vol. 31, pp. 307–327.
Day, T.E. and Lewis, C.M., Forecasting Futures Market Volatility, J. Derivatives, 1993, vol. 1, pp. 33–50.
Duan, J.C., The GARCH Option Pricing Model, Math. Finance, 1995, vol. 5, no.1, pp. 13–32.
Hamilton, J.D., Time Series Analysis, Princeton: Princeton Univ. Press, 1994.
Bollerslev, T., Chou, R.Y., and Kroner, K.F., ARCH Modeling in Finance: A Review of the Theory and Empirical Evidence, J. Econometrics, 1992, vol. 52, pp. 5–59.
Engle, R., Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation, Econometrica, 1982, vol. 50, pp. 987–1007.
Liptser, R. and Khasminskii, R., On-line Estimation of a Smooth Regression Function, Teor. Veroyatn. Primen., 2002, vol. 47, no.3, pp. 567–594.
Goldentayer, L. and Liptser, R., On-line Tracking of a Smooth Regression Function, Stat. Inference Stoch. Process., to appear.
Mercurio, D. and Spokoiny, V., Statistical Inference for Time-Inhomogeneous Volatility Models, Preprint of Weierstrass Inst. for Applied Analysis and Stochastics, 2000, no. 583. Avaiable at www.wias-berlin.de/publications/preprints/index-2000.html.
Ibragimov, I. and Khasminskii, R., On Nonparametric Estimation of Regression, Doklady Akad. Nauk SSSR, 1980, vol. 252, no.4, pp. 780–784 [Soviet Math. Dokl. (Engl. Transl.), 1980, vol. 21, pp. 810–814].
Ibragimov, I.A. and Khas'minskii, R.Z., Asimptoticheskaya teoriya otsenivaniya, Moscow: Nauka, 1979. Translated under the title Statistical Estimation. Asymptotic Theory, New York: Springer, 1981.
Stone, C., Optimal Global Rates of Convergence for Nonparametric Regression, Ann. Statist., 1982, vol. 10, pp. 1040–1053.
Goldenshluger, A. and Nemirovski, A., Adaptive De-noising of Signals Satisfying Differential Inequalities, IEEE Trans. Inform. Theory, 1997, vol. 43, no.3, pp. 873–889.
Chow, P.L., Khasminskii, R., and Liptser, R., Tracking of Signal and Its Derivatives in the Gaussian White Noise, Stochastic Process. Appl., 1997, vol. 69, no.2, pp. 259–273.
Author information
Authors and Affiliations
Additional information
__________
Translated from Problemy Peredachi Informatsii, No. 3, 2005, pp. 32–50.
Original Russian Text Copyright © 2005 by Goldentayer, Klebaner, Liptser.
Rights and permissions
About this article
Cite this article
Goldentayer, L., Klebaner, F. & Liptser, R.S. Tracking Volatility. Probl Inf Transm 41, 212–229 (2005). https://doi.org/10.1007/s11122-005-0026-2
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/s11122-005-0026-2