Skip to main content

Advertisement

Springer Nature Link
Log in

Non-Markovian entanglement dynamics of two qubits interacting with a common electromagnetic field

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

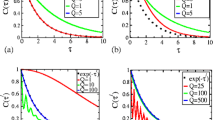
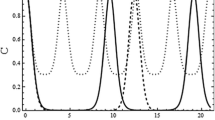
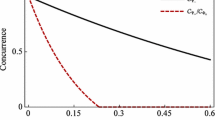
We study the non-equilibrium dynamics of a pair of qubits made of two-level atoms separated in space with distance r and interacting with one common electromagnetic field but not directly with each other. Our calculation makes a weak coupling assumption but no Born or Markov approximation. We write the evolution equations of the reduced density matrix of the two-qubit system after integrating out the electromagnetic field modes. We study two classes of states in detail: Class A is a one parameter family of states which are the superposition of the highest energy and lowest energy states, and Class B states which are the linear combinations of the symmetric and the antisymmetric Bell states. Our results for an initial Bell state are similar to those obtained before for the same model derived under the Born–Markov approximation. However, in the Class A states the behavior is qualitatively different: under the non-Markovian evolution we do not see sudden death of quantum entanglement and subsequent revivals, except when the qubits are sufficiently far apart. We provide explanations for such differences of behavior both between these two classes of states and between the predictions from the Markov and non-Markovian dynamics. We also study the decoherence of this two-qubit system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Paz, J.P., Zurek, W.H.: Coherent Atomic Matter Waves. In: Kaiser, R., Westbrook, C., David, F. (eds.) Proceedings of the Les Houches Summer School, Session LXXII, 1999, pp. 553–614. Springer, Berlin (2001)

  2. Zurek W.H.: Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 75, 715 (2003)

    Article  MathSciNet  ADS  Google Scholar 

  3. Horodecki R., Horodecki P., Horodecki M., Horodecki K.: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009)

    Article  CAS  MathSciNet  ADS  Google Scholar 

  4. Ficek Z., Tanas R.: Entangled states and collective nonclassical effects in two-atom systems. Phys. Rep. 372, 369 (2002)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  5. Anastopoulos C., Hu B.L.: Two-level atom–field interaction: exact master equations for non- Markovian dynamics, decoherence, and relaxation. Phys. Rev. A 62, 033821 (2000)

    Article  ADS  Google Scholar 

  6. Shresta S., Anastopoulos C., Dragulescu A., Hu B.L.: Non-Markovian qubit dynamics in a thermal field bath: relaxation, decoherence, and entanglement. Phys. Rev. A 71, 022109 (2005)

    Article  ADS  Google Scholar 

  7. Cummings N., Hu B.L.: Dynamics of atom–field entanglement: towards strong coupling and non-Markovian regimes. Phys. Rev. A 77, 053823 (2008)

    Article  ADS  Google Scholar 

  8. Zyczkowski K., Horodecki P., Horodecki M., Horodecki R.: Dynamics of quantum entanglement. Phys. Rev. A 65, 012101 (2001)

    Article  MathSciNet  ADS  Google Scholar 

  9. Yu T., Eberly J.H.: Finite-time disentanglement via spontaneous emission. Phys. Rev. Lett. 93, 140404 (2004)

    Article  PubMed  ADS  Google Scholar 

  10. Yu T., Eberly J.H.: Phonon decoherence of quantum entanglement: robust and fragile states. Phys. Rev. B 66, 193306 (2002)

    Article  ADS  Google Scholar 

  11. Yu T., Eberly J.H.: Qubit disentanglement and decoherence via dephasing. Phys. Rev. B 68, 165322 (2003)

    Article  ADS  Google Scholar 

  12. Ficek Z., Tanas R.: Dark periods and revivals of entanglement in a two-qubit system. Phys. Rev. A 74, 024304 (2006)

    Article  ADS  Google Scholar 

  13. Anastopoulos C., Shresta S., Hu B.L.: Quantum entanglement under non-Markovian dynamics of two qubits interacting with a common electromagnetic field. quant-ph/0610007

  14. Bell J.S.: On the Einstein podolsky rosen paradox. Physics 1, 195 (1964)

    Google Scholar 

  15. Wooters W.K.: Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245 (1998)

    Article  ADS  Google Scholar 

  16. Maniscalco S., Francica F., Zaffino R.L., Lo Gullo N., Plastina F.: Protecting entanglement via the quantum zeno Effect. Phys. Rev. Lett. 100, 090503 (2008)

    Article  PubMed  MathSciNet  ADS  Google Scholar 

  17. Piilo J., Maniscalco S., Harkonen K., Suominen K.-A.: Non-Markovian quantum jumps. Phys. Rev. Lett. 100, 180402 (2008)

    Article  PubMed  MathSciNet  ADS  Google Scholar 

  18. Paz J.P., Roncaglia A.J.: Dynamics of the entanglement between two oscillators in the same environment. Phys. Rev. Lett. 100, 220401 (2008)

    Article  PubMed  ADS  Google Scholar 

  19. Paz J.P., Roncaglia A.J.: Dynamical phases for the evolution of the entanglement between two oscillators coupled to the same environment. Phys. Rev. A 79, 032102 (2009)

    Article  ADS  Google Scholar 

  20. Lin S.Y., Hu B.L.: Temporal and spatial dependence of quantum entanglement from a field theory perspective. Phys. Rev. D 79, 085020 (2009)

    Article  ADS  Google Scholar 

  21. Yu, T., Eberly, J.H.: Many-body separability of warm qubits [arXiv:0707.3215]

Download references

Author information

Author notes

  1. S. Shresta

    Present address: MITRE Corporation, 7515 Colshire Drive, MailStop N390, McLean, VA, 22102, USA

Authors and Affiliations

  1. Department of Physics, University of Patras, 26500, Patras, Greece

    C. Anastopoulos

  2. Joint Quantum Institute, Department of Physics, University of Maryland, College Park, MD, 20742-4111, USA

    S. Shresta

  3. Atomic Physics Division, NIST, Gaithersburg, MD, 20899-8423, USA

    S. Shresta & B. L. Hu

Authors
  1. C. Anastopoulos
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. S. Shresta
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. B. L. Hu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to C. Anastopoulos.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Anastopoulos, C., Shresta, S. & Hu, B.L. Non-Markovian entanglement dynamics of two qubits interacting with a common electromagnetic field. Quantum Inf Process 8, 549–563 (2009). https://doi.org/10.1007/s11128-009-0137-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-009-0137-6

Keywords

PACS