Skip to main content
Springer Nature Link
Log in

Experimentally feasible measures of distance between quantum operations

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

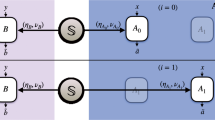
We present two measures of distance between quantum processes which can be measured directly in laboratory without resorting to process tomography. The measures are based on the superfidelity, introduced recently to provide an upper bound for quantum fidelity. We show that the introduced measures partially fulfill the requirements for distance measure between quantum processes. We also argue that they can be especially useful as diagnostic measures to get preliminary knowledge about imperfections in an experimental setup. In particular we provide quantum circuit which can be used to measure the superfidelity between quantum processes. We also provide a physical interpretation of the introduced metrics based on the continuity of channel capacity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Bengtsson I., Życzkowski K.: Geometry of Quantum States: An Introduction to Quantum Entanglement. Cambridge University Press, Cambridge (2006)

    Book  MATH  Google Scholar 

  2. Hayashi M.: Quantum Information: An Introduction. Springer, Berlin (2006)

    MATH  Google Scholar 

  3. Leonhardt U.: Discrete Wigner function and quantum-state tomography. Phys. Rev. A 53(5), 2998–3013 (1996)

    Article  CAS  MathSciNet  ADS  PubMed  Google Scholar 

  4. Jones K.R.W.: Principles of quantum inference. Ann. Phys. 207(1), 140–170 (1991)

    Article  ADS  Google Scholar 

  5. Poyatos J.F., Cirac J.I., Zoller P.: Complete characterization of a quantum process: the two-bit quantum gate. Phys. Rev. Lett. 78(2), 390–393 (1997)

    Article  CAS  ADS  Google Scholar 

  6. D’Ariano G.M., Lo Presti P.: Quantum tomography for measuring experimentally the matrix elements of an arbitrary quantum operation. Phys. Rev. Lett. 86(19), 4195–4198 (2001)

    Article  ADS  PubMed  CAS  Google Scholar 

  7. Acín A.: Statistical distinguishability between unitary operations. Phys. Rev. Lett. 87(17), 177901 (2001)

    Article  ADS  PubMed  CAS  Google Scholar 

  8. D’Ariano G.M., Sacchi M.F., Kahn J.: Minimax discrimination of two Pauli channels. Phys. Rev. A 72(5), 1 (2005)

    Google Scholar 

  9. Wang G., Ying M.: Unambiguous discrimination among quantum operations. Phys. Rev. A 73(4), 042301 (2006)

    Article  ADS  CAS  Google Scholar 

  10. Watrous J.: Distinguishing quantum operations having few Kraus operators. Quantum Inf. Comput. 8(8–9), 0819–0833 (2008)

    CAS  MathSciNet  Google Scholar 

  11. Chiribella G., D’Ariano G.M., Perinotti P.: Memory effects in quantum channel discrimination. Phys. Rev. Lett. 101, 180501 (2008)

    Article  MathSciNet  ADS  PubMed  CAS  Google Scholar 

  12. Gilchrist A., Langford N.K., Nielsen M.A.: Distance measures to compare real and ideal quantum processes. Phys. Rev. A 71(6), 062310 (2005)

    Article  ADS  CAS  Google Scholar 

  13. Belavkin V.P., D’Ariano G.M., Raginsky M.: Operational distance and fidelity for quantum channels. J. Math. Phys. 46, 062106 (2005)

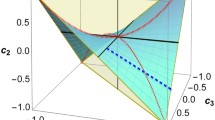
    Article  MathSciNet  ADS  CAS  Google Scholar 

  14. Miszczak J.A., Puchała Z., Horodecki P., Uhlmann A., Życzkowski K.: Sub- and super-fidelity as bounds for quantum fidelity. Quantum Inf. Comput. 9(1&2), 0103–0130 (2009)

    Google Scholar 

  15. Mendonca P.E.M.F., Napolitano R.d.J., Marchiolli M.A., Foster C.J., Liang Y.C.: An alternative fidelity measure for quantum states. Phys. Rev. A 78, 052330 (2008)

    Article  ADS  CAS  Google Scholar 

  16. Puchała Z., Miszczak J.A.: Bound on trace distance based on superfidelity. Phys. Rev. A 79, 024302 (2009)

    Article  MathSciNet  ADS  CAS  Google Scholar 

  17. Ekert A.K., Alves C.M., Oi D.K.L., Horodecki M., Horodecki P., Kwek L.C.: Direct estimations of linear and nonlinear functionals of a quantum state. Phys. Rev. Lett. 88(21), 217901 (2002)

    Article  ADS  PubMed  CAS  Google Scholar 

  18. Nielsen A., Chuang I.L.: Quantum Computation and Quantum Information. Quantum Computation and Quantum Information Cambridge University Press, Cambridge, UK (2000)

    MATH  Google Scholar 

  19. Banaszek, K.: Private communication

  20. Mohseni M., Rezakhani A.T., Lidar D.A.: Quantum-process tomography: resource analysis of different strategies. Phys. Rev. A 77(3), 32322 (2008)

    Article  ADS  CAS  Google Scholar 

  21. Leung D., Smith G.: Continuity of quantum channel capacities. Comm. Math. Phys. 292, 201–215 (2009)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  22. Kitaev A.Y., Shen A.H., Vyalyi M.N.: Classical and Quantum Computation Graduate Studies in Mathematics, vol. 47. American Mathematical Society, Providence (2002)

    Google Scholar 

  23. Aharonov, D. Kitaev, A., Nisan, N.: Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computation (STOC). pp. 20–30. ArXiv:quant-ph/9806029 (1998)

  24. Fujiwara A., Algoet P.: One-to-one parametrization of quantum channels. Phys. Rev. A 59(5), 3290–3294 (1999)

    Article  CAS  ADS  Google Scholar 

  25. Bruzda W., Cappellini V., Sommers H.J., Życzkowski K.: Random quantum operations. Phys. Lett. A 373(3), 320–324 (2009)

    Article  CAS  MathSciNet  ADS  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Theoretical and Applied Informatics, Polish Academy of Sciences, Bałtycka 5, 44-100, Gliwice, Poland

    Zbigniew Puchała, Jarosław Adam Miszczak, Piotr Gawron & Bartłomiej Gardas

Authors
  1. Zbigniew Puchała
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jarosław Adam Miszczak
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Piotr Gawron
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Bartłomiej Gardas
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Zbigniew Puchała.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Puchała, Z., Miszczak, J.A., Gawron, P. et al. Experimentally feasible measures of distance between quantum operations. Quantum Inf Process 10, 1–12 (2011). https://doi.org/10.1007/s11128-010-0166-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-010-0166-1

Keywords