Skip to main content

Advertisement

Springer Nature Link
Log in

Multiparty quantum key agreement with single particles

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

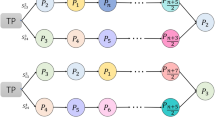
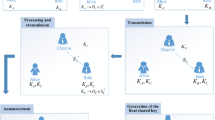
Abstract

Two conditions must be satisfied in a secure quantum key agreement (QKA) protocol: (1) outside eavesdroppers cannot gain the generated key without introducing any error; (2) the generated key cannot be determined by any non-trivial subset of the participants. That is, a secure QKA protocol can not only prevent the outside attackers from stealing the key, but also resist the attack from inside participants, i.e. some dishonest participants determine the key alone by illegal means. How to resist participant attack is an aporia in the design of QKA protocols, especially the multi-party ones. In this paper we present the first secure multiparty QKA protocol against both outside and participant attacks. Further more, we have proved its security in detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Menezes, A.J., van Oorscot, P.C., Vanstone, S.A.: Key establishment protocols. In: Handbook of Applied Cryptography. CRC Press, Boca Raton (1997)

  2. Mitchell C.J., Ward M., Wilson P.: Key control in key agreement protocols. Electron. Lett. 34(10), 980–981 (1998)

    Article  Google Scholar 

  3. Ateniese G., Steiner M., Tsudik G.: New multiparty authentication services and key agreement protocols. IEEE J. Sel. Areas Commun. 18(4), 628 (2000)

    Article  Google Scholar 

  4. Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings of 35th Annual Symposium on the Foundations of Computer Science, pp. 124–134, Santa Fe (1994)

  5. Grover, L.K.: A fast quantum mechanical algorithm for database search. In: Proceedings of 28th Annual ACM Symposium on Theory of Computing, pp. 212–219, New York (1996)

  6. Bennett, C.H., Brassard, G.: Quantum cryptography: public-key distribution and coin tossing. In: Proceedings of IEEE International Conference on Computers, Systems and Signal, pp. 175–179, Bangalore (1984)

  7. Jackson D.J., Hockney G.M.: Securing QKD links in the full Hilbert space. Quantum Inf. Process. 4, 35–47 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  8. Brandt H.E.: Unambiguous state discrimination in quantum key distribution. Quantum Inf. Process. 4, 387–398 (2005)

    Article  MathSciNet  ADS  Google Scholar 

  9. Gao F., Guo F.Z., Wen Q.Y., Zhu F.C.: On the information-splitting essence of two types of quantum key distribution protocols. Phys. Lett. A 355, 172–175 (2006)

    Article  ADS  MATH  Google Scholar 

  10. Huang W., Guo F.Z., Huang Z., Wen Q.Y., Zhu F.C.: Three-particle QKD protocol against a collective noise. Opt. Commun. 284(1), 536–540 (2011)

    Article  ADS  Google Scholar 

  11. Liu B., Gao F., Wen Q.Y.: Single-photon multiparty quantum cryptographic protocols with collective detection. IEEE J. Quant. Electron. 47, 1383–1390 (2011)

    Article  ADS  Google Scholar 

  12. El Allati A., El Baz M., Hassouni Y.: Quantum key distribution via tripartite coherent states. Quantum Inf. Process. 10, 589–602 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  13. Cleve R., Gottesman D., Lo H.K.: How to share a quantum secret. Phys. Rev. Lett. 83, 648–651 (1999)

    Article  ADS  Google Scholar 

  14. Hillery M., Buzěk V., Berthiaume A.: Quantum secret sharing. Phys. Rev. A 59, 1829–1834 (1999)

    Article  MathSciNet  ADS  Google Scholar 

  15. Karlsson A., Koashi M., Imoto N.: Quantum entanglement for secret sharing and secret splitting. Phys. Rev. A 59, 162–168 (1999)

    Article  ADS  Google Scholar 

  16. Gao F., Qin S.J., Wen Q.Y.: A simple participant attack on the Bradler–Dusek protocol. Quantum Inf. Comput. 7, 329–334 (2007)

    MathSciNet  MATH  Google Scholar 

  17. Qin S.J., Gao F., Wen Q.Y., zhu F.C.: Cryptanalysis of the Hillery–Buzek–Berthiaume quantum secret-sharing protocol. Phys. Rev. A 76, 062324 (2007)

    Article  ADS  Google Scholar 

  18. Song T.T., Zhang J., Gao F., Wen Q.Y., Zhu F.C.: Participant attack on quantum secret sharing based on entanglement swapping. Chin. Phys. B 18, 1333 (2009)

    Article  ADS  Google Scholar 

  19. Guo F.Z., Qin S.J., Gao F., Lin S., Wen Q.Y., Zhu F.C.: Participant attack on a kind of MQSS schemes based on entanglement swapping. Eur. Phys. J. D 56, 445 (2010)

    Article  ADS  Google Scholar 

  20. Yang Y., Wang Y., Chai H., Teng Y., Zhang H.: Member expansion in quantum (t,n) threshold secret sharing schemes. Opt. Commun. 284, 3479–3482 (2011)

    Article  ADS  Google Scholar 

  21. Shi R.H., Zhong H.: Multiparty quantum secret sharing with the pure entangled two-photon states. Quantum Inf. Process. 11, 161–169 (2012)

    Article  MathSciNet  Google Scholar 

  22. Long G., Liu X.: Theoretically efficient high-capacity quantum- key- distribution scheme. Phys. Rev. A 65, 032302 (2002)

    Article  ADS  Google Scholar 

  23. Boström K., Felbinger T.: Deterministic secure direct communication using entanglement. Phys. Rev. Lett. 89, 187902 (2002)

    Article  ADS  Google Scholar 

  24. Deng F., Long G., Liu X.: Two-step quantum direct communication protocol using the Einstein–Podolsky–Rosen pair block. Phys. Rev. A 68, 042317 (2003)

    Article  ADS  Google Scholar 

  25. Gao F., Qin S.J., Wen Q.Y., Zhu F.C.: Cryptanalysis of multiparty controlled quantum secure direct communication using Greenberger–Horne–Zeilinger state. Opt. Commun. 283, 192 (2010)

    Article  ADS  Google Scholar 

  26. Yang Y.G., Cao W.F., Wen Q.Y.: Secure quantum private comparison. Phsy. Scr. 80, 065002 (2009)

    Article  ADS  Google Scholar 

  27. Chen X.B., Xu G., Niu X.X., Wen Q.Y., Yang Y.X.: An efficient protocol for the private comparison of equal information based on the triplet entangled state and single-particle measurement. Opt. Commun. 283, 1161–1165 (2009)

    Google Scholar 

  28. Liu W., Wang Y.B., Jiang Z.T.: An efficient protocol for the quantum private comparison of equality with W state. Opt. Commun. 284, 3160–3163 (2011)

    Article  ADS  Google Scholar 

  29. Tseng H.Y., Lin J., Hwang T.: New quantum private comparison protocol using EPR pairs. Quantum Inf. Process. 11, 373–384 (2011)

    Article  MathSciNet  Google Scholar 

  30. Liu, B., Gao, F., Jia, H.Y., Huang, W., Zhang, W.W., Wen, Q.Y.: Efficient quantum private comparison employing single photons and collective detection. Quantum Inf. Process. (2012). doi:10.1007/s11128-012-0439-y

  31. Gao F., Wen Q.Y., Zhu F.C.: Comment on: “Quantum exam”. Phys. Lett. A 360, 748 (2007)

    Article  ADS  Google Scholar 

  32. Gao F., Guo F.Z., Wen Q.Y., Zhu F.C.: Comment on “Experimental Demonstration of a Quantum Protocol for Byzantine Agreement and Liar Detection”. Phys. Rev. Lett. 101, 208901 (2008)

    Article  ADS  Google Scholar 

  33. Gisin N., Ribordy G., Tittel W., Zbinden H.: Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002)

    Article  ADS  Google Scholar 

  34. Tajima A., Tanaka A., Maeda W., Takahashi S., Tomita A.: Practical quantum cryptosystem for metro area applications. IEEE J. Sel. Top. Quant. Electron. 13, 1031–1038 (2007)

    Article  Google Scholar 

  35. Zhou N., Zeng G., Xiong J.: Quantum key agreement protocol. Electron. Lett. 40, 1149 (2004)

    Article  Google Scholar 

  36. Chong S.K., Tsai C.W., Hwang T.: Improvement on quantum key agreement protocol with maximally entangled states. Int. J. Theor. Phys. 50, 1793–1802 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  37. Chong S.K., Hwang T.: Quantum key agreement protocol based on BB84. Opt. Commun. 283, 1192–1195 (2010)

    Article  ADS  Google Scholar 

  38. Shi, R.H., Zhong, H.: Multi-party quantum key agreement with bell states and bell measurements. Quantum Inf. Process. doi:10.1007/s11128-012-0443-2

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Bin Liu, Fei Gao, Wei Huang & Qiao-yan Wen

  2. State Key Laboratory of Information Security, Institute of Software, Chinese Academy of Sciences, Beijing, 100190, China

    Bin Liu & Fei Gao

Authors
  1. Bin Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Fei Gao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Wei Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Qiao-yan Wen
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Fei Gao.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liu, B., Gao, F., Huang, W. et al. Multiparty quantum key agreement with single particles. Quantum Inf Process 12, 1797–1805 (2013). https://doi.org/10.1007/s11128-012-0492-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-012-0492-6

Keywords