Skip to main content

Advertisement

Springer Nature Link
Log in

Stationary quantum correlations in Tavis–Cumming model induced by continuous dephasing process

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

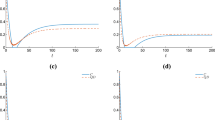
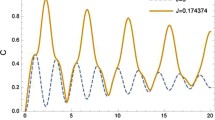
We investigate the dynamics of quantum correlations for the Tavis–Comming model in continuous dephasing process. It is shown that quantum discord and entanglement can reach stationary value, and quantum Zeno effect occurs in strong-coupling region. Furthermore, we explore the influence of continuous dephasing process on the trace distance between two marginal states of the two atoms and find that the trace distance also achieve a constant value during time evolution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Wheeler, J.A., Zurek, W.H.: Quantum Theory of Measurement. Princeton University Press, Princeton (1983)

    Google Scholar 

  2. Braginsky, V.B., Khalili, F. Ya.: Quantum Measurement. Cambridge University Press, Cambridge (1992)

  3. Onofrio, R., Viola, L.: Lindblad approach to nonlinear Jaynes-Cummings dynamics of a trapped ion. Phys. Rev. A. 56, 39–43 (1997)

    Article  ADS  Google Scholar 

  4. Brun, T.A.: Continuous measurements, quantum trajectories, and decoherent histories. Phys. Rev. A. 61(4), 042107 (2000)

    Article  MathSciNet  ADS  Google Scholar 

  5. Greenberger, D.M.: New Techniques and Ideas in Quantum Measurement Theory, pp. 663–664. New York Academy of Science, New York (1986)

    Google Scholar 

  6. Lindblad, G.: On the generators of quantum dynamical semigroups. Commun. Math. Phys. 48, 119–130 (1976)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  7. Korotkov, A.N.: Selective quantum evolution of a qubit state due to continuous measurement. Phys. Rev. B. 63(11), 115403 (2001)

    Article  ADS  Google Scholar 

  8. Sun, C.P., Liu, X.F., Zhou, D.L., Yu, S.X.: Quantum measurement via born-oppenheimer adiabatic dynamics. Phys. Rev. A. 63(1), 012111 (2000)

    Article  ADS  Google Scholar 

  9. Goan, H.-S., Milburn, G.J., Wiseman, H.M., Sun, H.B.: Continuous quantum measurement of two coupled quantum dots using a point contact: a quantum trajectory approach. Phys. Rev. B. 63(12), 125326 (2001)

    Article  ADS  Google Scholar 

  10. Einstein, A., Podolsky, B., Rosen, N.: Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935)

    Article  ADS  MATH  Google Scholar 

  11. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Communication, pp. 353–354. Cambridge University Press, Cambridge (2000)

    Google Scholar 

  12. Bose, S., Fuentes-Guridi, I., Knight, P.L., Vedral, V.: Subsystem purity as an enforcer of entanglement. Phys. Rev. Lett. 87(5), 050401 (2001)

    Article  MathSciNet  ADS  Google Scholar 

  13. Kim, M.S., Lee, J.Y., Ahn, D., Knight, P.L.: Entanglement induced by a single-mode heat environment. Phys. Rev. A. 65(4), 040101 (2002)

    Article  ADS  Google Scholar 

  14. Jones, J., et al.: Implementation of a quantum search algorithm on a quantum computer. Nat. (London) 393, 344–346 (1998)

    Article  ADS  Google Scholar 

  15. Paternostro, M., Vitali, D., Gigan, S., Kim, M.S., Brukner, C., Eisert, J., Aspelmeyer, M.: Creating and probing multipartite macroscopic entanglement with light. Phys. Rev. Lett. 99(25), 250401 (2007)

    Article  ADS  Google Scholar 

  16. Vitali, D., Gigan, S., Ferreira, A., Bohm, H.R., Tombesi, P., Guerreiro, A., Vedral, V., Zeilinger, A., Aspelmeyer, M.: Optomechanical entanglement between a movable mirror and a cavity field. Phys. Rev. Lett. 98(3), 030405 (2007)

    Article  ADS  Google Scholar 

  17. Horodecki, M., Horodecki, P., Horodecki, R., Oppenheim, J., Sen, A., Sen, U., Synak-Radtke, B.: Local versus nonlocal information in quantum-information theory: formalism and phenomena. Phys. Rev. A. 71(6), 062307 (2005)

    Article  ADS  Google Scholar 

  18. Niset, J., Cerf, N.J.: Multipartite nonlocality without entanglement in many dimensions. Phys. Rev. A. 74(5), 052103 (2006)

    Article  ADS  Google Scholar 

  19. Passante, G., Moussa, O., Trottier, D.A., Laflamme, R.: Experimental detection of nonclassical correlations in mixed-state quantum computation. Phys. Rev. A. 84(4), 044302 (2011)

    Article  ADS  Google Scholar 

  20. Ollivier, H., Zurek, W.H.: Quantum discord: a measure of the quantumness of correlations. Phys. Rev. Lett. 88(4), 017901 (2002)

    ADS  Google Scholar 

  21. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  22. Gilchrist, A., Langford, N.K., Nielsen, M.A.: Distance measures to compare real and ideal quantum processes. Phys. Rev. A. 71(6), 062310 (2005)

    Article  ADS  Google Scholar 

  23. Breuer, H.-P., Laine, E.-M., Piilo, J.: Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 103(21), 210401 (2009)

    Article  MathSciNet  ADS  Google Scholar 

  24. Laine, E.-M., Piilo, J., Breuer, H.-P.: Measure for the non-Markovianity of quantum processes. Phys. Rev. A. 81(6), 062115 (2010)

    Article  ADS  Google Scholar 

  25. Liu, B.-H., Huang, Y.-F., Li, C.-F., Guo, G.-C., Laine, E.-M., Breuer, H.-P., Piilo, J.: Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems. Nat. Phys. 7, 931–934 (2011)

    Article  Google Scholar 

  26. Tavis, M., Cummings, F.W.: Exact solution for an N-molecule radiation-field Hamiltonian. Phys. Rev. 170, 379–384 (1968)

    Article  ADS  Google Scholar 

  27. Guo, J.-L., Song, H.-S.: Dynamics of pairwise entanglement between two TavisC-Cummings atoms. J. Phys. A: Math. Theor. 41, 085302 (2008)

    Article  MathSciNet  ADS  Google Scholar 

  28. Misra, B., Sudarshan, E.C.G.: The Zenos paradox in quantum theory. J. Math. Phys. 18, 756 (1977)

    Article  MathSciNet  ADS  Google Scholar 

  29. Facchi, P., Nakazato, H., Pascazio, S.: From the quantum zeno to the inverse quantum zeno effect. Phys. Rev. Lett. 86(13), 2699 (2001)

    Article  ADS  Google Scholar 

  30. Facchi, P., et al.: Control of decoherence: analysis and comparison of three different strategies. Phys. Rev. A. 71(2), 022302 (2005)

    Article  ADS  Google Scholar 

  31. Dalibard, J., Castin, Y., Molmer, K.: Wave-function approach to dissipative processes. Phys. Rev. Lett. 68, 580–583 (1992)

    Article  ADS  Google Scholar 

  32. Ali, M., Rau, A.R.P., Alber, G.: Quantum discord for two-qubit X states. Phys. Rev. A. 81(4), 042105 (2010)

    Article  ADS  Google Scholar 

  33. Wootters, W.K.: Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248 (1998)

    Article  ADS  Google Scholar 

  34. Yu, T., Eberly, J.H.: Evolution from entanglement to decoherence. Quantum Inf. Comput. 7, 459–468 (2007)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This project was supported by the National Natural Science Foundation of China (Grant No. 11274274).

Author information

Authors and Affiliations

  1. Zhejiang Institute of Modern Physics and Physics Department, Zhejiang University, Hangzhou, 310027, China

    Wei Wu, Hang-Shi Xu, Zheng-Da Hu & Jing-Bo Xu

Authors
  1. Wei Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hang-Shi Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Zheng-Da Hu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jing-Bo Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jing-Bo Xu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wu, W., Xu, HS., Hu, ZD. et al. Stationary quantum correlations in Tavis–Cumming model induced by continuous dephasing process. Quantum Inf Process 12, 3191–3206 (2013). https://doi.org/10.1007/s11128-013-0596-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-013-0596-7

Keywords