Bidirectional controlled quantum teleportation and secure direct communication using five-qubit entangled state

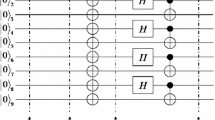
Abstract

A scheme is presented to implement bidirectional controlled quantum teleportation (QT) by using a five-qubit entangled state as a quantum channel, where Alice may transmit an arbitrary single qubit state called qubit A to Bob and at the same time, Bob may also transmit an arbitrary single qubit state called qubit B to Alice via the control of the supervisor Charlie. Based on our channel, we explicitly show how the bidirectional controlled QT protocol works. By using this bidirectional controlled teleportation, espcially, a bidirectional controlled quantum secure direct communication (QSDC) protocol, i.e., the so-called controlled quantum dialogue, is further investigated. Under the situation of insuring the security of the quantum channel, Alice (Bob) encodes a secret message directly on a sequence of qubit states and transmits them to Bob (Alice) supervised by Charlie. Especially, the qubits carrying the secret message do not need to be transmitted in quantum channel. At last, we show this QSDC scheme may be determinate and secure.

Appendix

Alice’s possible measurement result, Bob’s possible measurement result, Charlie’s possible measurement result, final state with the corresponding transformation performed by Alice and Bob on qubits 4 and 3, respectively, where $\sigma ^{i},i\in \left\{ {x,y,z} \right\}$ are Pauli matrices.

Alice’s result	Bob’s result	Charlie’s result	Final state with the receiver	Unitary transformation corresponding to the measurement outcomes (++, $+-, -+, -$)
$\left| {\Phi ^{\pm }} \right\rangle _{A1}$	$\left| {\Phi ^{\pm }} \right\rangle _{B2}$	$\left| 0 \right\rangle _5$	$\left( {b_0 \left| 1 \right\rangle \pm b_1 \left| 0 \right\rangle } \right) _4 \otimes \left( {a_0 \left| 0 \right\rangle \pm a_1 \left| 1 \right\rangle } \right) _3$	$\sigma _4^x \otimes I_3, \sigma _4^x \otimes \sigma _3^z, -i\sigma _4^y \otimes I_3, -i\sigma _4^y \otimes \sigma _3^z$
$\left| {\Phi ^{\pm }} \right\rangle _{A1}$	$\left| {\Psi ^{\pm }} \right\rangle _{B2}$	$\left| 0 \right\rangle _5$	$\left( {b_0 \left| 0 \right\rangle \pm b_1 \left| 1 \right\rangle } \right) _4 \otimes \left( {a_0 \left| 0 \right\rangle \pm a_1 \left| 1 \right\rangle } \right) _3$	$I_4 \otimes I_3, I_4 \otimes \sigma _3^z, \sigma _4^z \otimes I_3, \sigma _4^z \otimes \sigma _3^z$
$\left| {\Psi ^{\pm }} \right\rangle _{A1}$	$\left| {\Phi ^{\pm }} \right\rangle _{B2}$	$\left| 0 \right\rangle _5$	$\left( {b_0 \left| 1 \right\rangle \pm b_1 \left| 0 \right\rangle } \right) _4 \otimes \left( {a_0 \left| 1 \right\rangle \pm a_1 \left| 0 \right\rangle } \right) _3$	$\sigma _4^x \otimes \sigma _3^x, \sigma _4^x \otimes -i\sigma _3^y, -i\sigma _4^y \otimes \sigma _3^x, -i\sigma _4^y \otimes -i\sigma _3^y$
$\left| {\Psi ^{\pm }} \right\rangle _{A1}$	$\left| {\Psi ^{\pm }} \right\rangle _{B2}$	$\left| 0 \right\rangle _5$	$\left( {b_0 \left| 0 \right\rangle \pm b_1 \left| 1 \right\rangle } \right) _4 \otimes \left( {a_0 \left| 1 \right\rangle \pm a_1 \left| 0 \right\rangle } \right) _3$	$I_4 \otimes \sigma _3^x, I_4 \otimes -i\sigma _3^y, \sigma _4^z \otimes \sigma _3^x, \sigma _4^z \otimes -i\sigma _3^y$
$\left| {\Phi ^{\pm }} \right\rangle _{A1}$	$\left| {\Phi ^{\pm }} \right\rangle _{B2}$	$\left| 1 \right\rangle _5$	$\left( {b_0 \left| 0 \right\rangle \mp b_1 \left| 1 \right\rangle } \right) _4 \otimes \left( {a_0 \left| 1 \right\rangle \pm a_1 \left| 0 \right\rangle } \right) _3$	$\sigma _4^z \otimes \sigma _3^x, \sigma _4^z \otimes -i\sigma _3^y, I_4 \otimes \sigma _3^x, I_4 \otimes -i\sigma _3^y$
$\left| {\Phi ^{\pm }} \right\rangle _{A1}$	$\left| {\Psi ^{\pm }} \right\rangle _{B2}$	$\left| 1 \right\rangle _5$	$-\left( {b_0 \left| 1 \right\rangle \mp b_1 \left| 0 \right\rangle } \right) _4 \otimes \left( {a_0 \left| 1 \right\rangle \pm a_1 \left| 0 \right\rangle } \right) _3$	$\sigma _4^z \sigma _4^x \otimes \sigma _3^x, \sigma _4^z \sigma _4^x \otimes -i\sigma _3^y, -i\sigma _4^y \sigma _4^z \otimes \sigma _3^x, -i\sigma _4^y \sigma _4^z \otimes -i\sigma _3^y$
$\left| {\Psi ^{\pm }} \right\rangle _{A1}$	$\left| {\Phi ^{\pm }} \right\rangle _{B2}$	$\left| 1 \right\rangle _5$	$\left( {b_0 \left| 0 \right\rangle \mp b_1 \left| 1 \right\rangle } \right) _4 \otimes \left( {a_0 \left| 0 \right\rangle \pm a_1 \left| 1 \right\rangle } \right) _3$	$\sigma _4^z \otimes I_3, \sigma _4^z \otimes \sigma _3^z, I_4 \otimes I_3, I_4 \otimes \sigma _3^z$
$\left| {\Psi ^{\pm }} \right\rangle _{A1}$	$\left| {\Psi ^{\pm }} \right\rangle _{B2}$	$\left| 1 \right\rangle _5$	$-\left( {b_0 \left| 1 \right\rangle \mp b_1 \left| 0 \right\rangle } \right) _4 \otimes \left( {a_0 \left| 0 \right\rangle \pm a_1 \left| 1 \right\rangle } \right) _3$	$\sigma _4^z \sigma _4^x \otimes I_3, \sigma _4^z \sigma _4^x \otimes \sigma _3^z, -i\sigma _4^y \sigma _4^z \otimes I_3, -i\sigma _4^y \sigma _4^z \otimes \sigma _3^z$