Local deterministic simulation of equatorial Von Neumann measurements on tripartite GHZ state

Abstract

Experimental free-will or measurement independence is one of the crucial assumptions in derivation of any nonlocal theorem. Any nonlocal correlation obtained in quantum world can have a local deterministic explanation if there is no experimental free-will in choosing the measurement settings. Recently, Hall (Phys Rev Lett 105:250404, 2010) has shown that to obtain a local deterministic description for singlet state correlation one does not need to give up measurement independence completely, but a partial measurement dependence suffices. In three party scenario considering Greenberger–Horne–Zeilinger (GHZ) correlation one can exhibit absolute contradiction between quantum theory and local realism. In this paper we show that such correlation also has local deterministic description if measurement independence is given up, even if not completely. We provide a local deterministic model for equatorial Von Neumann measurements on tripartite GHZ state by sacrificing measurement independence partially.

Appendices

Appendix 1: Calculation of measurement dependency

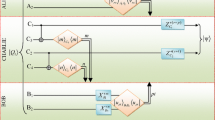
The degree of measurement dependency is quantified as Eq. (8). To find $M$ we have to maximize the difference between the densities of hidden variable (HV) for all pairs of measurement settings over the HV space. The difference will be maximized if the upper value of the distribution of HV corresponding to one measurement setting overlaps by maximum amount with the lower value of the other measurement setting. The distribution of HV for each measurement setting consists of three pair of regions comprising two opposite spherical sectors ({$R_{1+},R_{1-}$},{$R_{2+},R_{2-}$},{$R_{3+},R_{3-}$}) and a pair of delta functions ($D_+,D_-$) as defined in Eq. (13)and shown in Fig. 2. The distribution of HV for measurement setting $\{\hat{m}_X\}$ and $\{\hat{m}_X^{\prime }\}$ are denoted by prime and unprimed region, respectively (see Fig. 3). The maximum of right hand side of Eq. (8) occurs when $R_{1+}$ contains $D_-^{\prime }$ and the region $R_{3-}^{\prime }$ completely and the region $R_{2-}^{\prime }$ partially as shown in Fig. 3. It becomes that $M=1.43$ and thus we have $F:=1-\frac{M}{2}\simeq$ 28.5 %.

Fig. 2

(Color on-line). $R_{1+} (R_{1-})$ is the region where $s(\hat{m}_A.\varvec{\lambda })=s(\hat{m}_B.\varvec{\lambda })= s(\hat{m}_C.\varvec{\lambda })=+1 (-1)$; $R_{2+} (R_{2-})$ is the region where $s(\hat{m}_A.\varvec{\lambda })=-s(\hat{m}_B.\varvec{\lambda })= -s(\hat{m}_C.\varvec{\lambda })=+1 (-1)$ and $R_{3+} (R_{3-})$ is the region where $-s(\hat{m}_A.\varvec{\lambda })=-s(\hat{m}_B. \varvec{\lambda })=s(\hat{m}_C.\varvec{\lambda })=+1 (-1)$. $D_+$ ($D_{-}$) denotes the fixed vector $\varvec{\lambda _0}$ (-$\varvec{\lambda _0}$)

Fig. 3

(Color on-line). This figure shows distribution of HV corresponding to measurement settings $\{\hat{m}_X\}$ and $\{\hat{m}_X^{\prime }\}$. The inner circle represents the distribution corresponding to the measurement setting $\{\hat{m}_X^{\prime }\}$ and the outer circle corresponding to the measurement setting $\{\hat{m}_X\}$. The maximum of the right hand side of Eq. (8) occurs when $R_{1+}$ contains $D_-^{\prime }$ and the region $R_{3-}^{\prime }$ completely and the region $R_{2-}^{\prime }$ partially

Appendix 2: Simulation of GHZ expectation value

In this case also Alice, Bob and Charlie share a variable $\varvec{\lambda }$ chosen from unit circle and given a measurement direction from equatorial plane Alice, Bob and Charlie give there answer like Eq. (10). The distribution of the variable $\varvec{\lambda }$ in this case is given by

$$\begin{aligned} \vartheta (\varvec{\lambda }|\{\hat{m}_X\})&:= \vartheta ^{\prime }(\varvec{\lambda } |\{\hat{m}_X\})\varTheta (\phi _{AB}-\phi _{AC})\\&\quad +\vartheta ^{\prime \prime }(\varvec{\lambda }|\{\hat{m}_X\})\varTheta (\phi _{AC}-\phi _{AB}), \end{aligned}$$

where

$$\begin{aligned} \vartheta ^{\prime }(\varvec{\lambda }|\{\hat{m}_X\}):&= \frac{1+\beta \cos (\phi _A+\phi _B+\phi _C)}{6(\pi -\phi _{AB})}\nonumber \\&\text{ if } s(\hat{m}_A.\varvec{\lambda })=s(\hat{m}_B.\varvec{\lambda }) =s(\hat{m}_C.\varvec{\lambda })=\beta \nonumber \\ :&= \frac{1+\beta \cos (\phi _A+\phi _B+\phi _C)}{6(\phi _{AB}- \phi _{AC})}\nonumber \\&\text{ if } -s(\hat{m}_A.\varvec{\lambda })=-s(\hat{m}_B. \varvec{\lambda })=s(\hat{m}_C.\varvec{\lambda })=\beta \nonumber \\ :&= \frac{1+\beta \cos (\phi _A+\phi _B+\phi _C)}{6\phi _{AB}}\nonumber \\&\text{ if } s(\hat{m}_A.\varvec{\lambda })=-s(\hat{m}_B. \varvec{\lambda })=-s(\hat{m}_C.\varvec{\lambda })=\beta \end{aligned}$$

with $\beta \in \{+1,-1\}$; and

$$\begin{aligned} \vartheta ^{\prime \prime }(\varvec{\lambda }|\{\hat{m}_X\}):&= \frac{1+\beta \cos (\phi _A+\phi _B+\phi _C)}{6(\pi -\phi _{AC})}\nonumber \\&\text{ if } s(\hat{m}_A.\varvec{\lambda })=s(\hat{m}_B.\varvec{\lambda }) =s(\hat{m}_C.\varvec{\lambda })=\beta \nonumber \\ :&= \frac{1+\beta \cos (\phi _A+\phi _B+\phi _C)}{6\phi _{AC}}\nonumber \\&\text{ if } s(\hat{m}_A.\varvec{\lambda })=-s(\hat{m}_B.\varvec{\lambda }) =-s(\hat{m}_C.\varvec{\lambda })=\beta \nonumber \\ :&= \frac{1+\beta \cos (\phi _A+\phi _B+\phi _C)}{6(\phi _{AC}- \phi _{AB})}\nonumber \\&\text{ if } -s(\hat{m}_A.\varvec{\lambda })=s(\hat{m}_B.\varvec{\lambda }) =-s(\hat{m}_C.\varvec{\lambda })=\beta . \end{aligned}$$

In this case it becomes $F=$ 37.5 %. Therefore 62.5 % lack of measurement independence for each party is sufficient to simulate statistic of the equatorial Von Neumann measurements on GHZ state.