Abstract
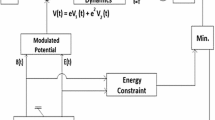
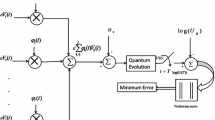
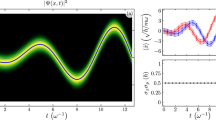
This paper deals with the approximate design of quantum unitary gates using perturbed harmonic oscillator dynamics. The harmonic oscillator dynamics is perturbed by a small time-varying electric field which leads to time-dependent Schrödinger equation. The corresponding unitary evolution after time T is obtained by approximately solving the time-dependent Schrödinger equation. The aim of this work is to minimize the discrepancy between a given unitary gate and the gate obtained by evolving the oscillator in the weak electric field over [0, T]. The proposed algorithm shows that the approximate design is able to realize the Hadamard gate and controlled unitary gate on three-qubit arrays with high accuracy.

Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Schiff, L.I.: Quantum Mechanics, 3rd edn. McGraw Hill, New York (1955)
Dirac, P.A.M.: The Principles of Quantum Mechanics, 4th edn, pp. 108–178. Oxford University Press, New York (1958)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2001)
Pavicic, M.: Quantum Computation and Quantum Communication: Theory and Experiments. Springer (2006)
Nakahara, M., Ohmi, T.: Quantum Computing: From Linear Algebra to Physical Realizations. CRC Press, Boca Raton (2008)
McMahon, D.: Quantum Computing Explained. Wiley, New York (2007)
Barenco, A., Bennett, C.H., Cleve, R., DiVincenzo, D.P., Margolus, N., Shor, P., Sleator, T., Smolin, J.A., Weinfurter, H.: Elementary gates for quantum computation. Phys. Rev. A 52, 3457–3467 (1995)
Perelomov, A.M.: Superpositions of the \(SU(1, 1)\). Phys. Lett. A 193, 121–125 (1994)
Glauber, R.J.: Coherent and incoherent states of radiation field. Phys. Rev. 131, 2766–2788 (1963)
Fox, M.: Quantum Optics: An Introduction, vol. 6. Oxford University Press, New York (2005)
Klauder, J.R., Skagerstam, B.: Coherent States. World Scientific, Singapore (1985)
Perelomov, A.M.: Generalized Coherent States and Their Applications Texts and Monographs in Physics. Springer, New York (1986)
Gazeau, J.P.: Coherent States in Quantum Physics. Wiley-VCH, Berlin (2009)
Zhang, W., Feng, D., Gilmore, R.: Coherent states—theory and some applications. Rev. Mod. Phys. 62, 867–927 (1990)
Combescure, M., Robert, D.: Coherent States and Applications, Mathematical Physics. Springer, New York (2012)
Ali, S.T., Antoine, J.P., Bagarello, F., Gazeau, J.P.: Coherent states: a contemporary panorama. J. Phys. A Math. Theor. 45, 240301 (2012)
Kato, T.: Perturbation Theory for Linear Operators, 2nd edn. Springer, Berlin (1980)
Kamran, N., Olver, P.J.: Lie algebras of differential operators and Lie-algebraic potentials. J. Math. Anal. Appl. 145, 342–356 (1990)
Bach, V.: Schrödinger operators. Encycl. Math. Phys. 1, 487–494 (2006)
Altafini, C.: On the generation of sequential unitary gates from continuous time Schrödinger equations driven by external fields. Quantum Inf. Process. 1, 207–224 (2002)
Zhang, Y., Kauffman, L.H., Ge, M., Baxterizations, Y.: Universal quantum gates and Hamiltonians. Quant. Inf. Process. 4, 159–197 (2005)
Altafini, C.: Parameter differentiation and quantum state decomposition for time varying Schrödinger equations. Rep. Math. Phys. 52(3), 381–400 (2003)
Hirota, O.: Some remarks on a conditional unitary operator. Phys. Lett. A 155(6–7), 343–347 (1991)
Parthasarathy, H.: Mathematical Ideas for Signal Processing Application. I.K. International Publishing House, New Delhi (2013)
Shepherd, D.J.: On the role of Hadamard gates in quantum circuits. Quantum Inf. Process. 5, 161–177 (2006)
Mohammad, N.S., Mehmandoost, M.: Realization of quantum Hadamard gate by applying optimal control fields to a spin qubit. In: 2nd International Conference on Mechanical and Electronics Engineering, vol. 2, pp. 292–296 (2010)
Kumar, P.: Direct implementation of an N-qubit controlled-unitary gate in a single step. Quantum Inf. Process. 12, 1201–1223 (2013)
Altintas, A.A., Ozaydin, F., Yesilyurt, C., Bugu, S., Arik, M.: Constructing quantum logic gates using q-deformed harmonic oscillator algebras. Quantum Inf. Process. 12, 1035–1044 (2014)
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
Referring to Eq. (6)
The gate error energy is given by (refer “Appendix 1”)
where
Expanding this Frobenius norm, we get
Note that
We calculate the variational derivative with respect to \(\widetilde{V}(t)\) of the last function taking into account energy constraint using Lagrange’s multiplier. The energy constraint
must be expressed in terms of \(\widetilde{V}(t)\). Using
this constraint becomes
where \(A(t)= \hbox {e}^{iH_0t} A \hbox {e}^{-iH_0t}\). The quantity to be minimized is
where \(\lambda \) is the Lagrange multiplier. We set the variational derivative of the above equation with respect to \(\widetilde{V}(t)\) to zero. The coefficient of \(\delta \widetilde{V}(t_2)\) is
Differentiate with respect to \(t_2\) and replace it by t,
We have assumed that A(t) is constant operator in order to simplify the calculations and replacing \(\epsilon \) by 1, \(\widetilde{V}\) by V and \({\widetilde{{U}_\mathrm{d}}}\) by \(U_\mathrm{d}\).
Appendix 2
Referring to Eq. (9)
The time-dependent Schrödinger equation in Eq. (39) leads to
where \(\langle m |x U(t)| n\rangle = \sum _{r=0}^{N-1} x_{mr} U_{rn} (t)\)
where
Let \(U_{mn} (t) = \hbox {e}^{-iE_mt}W_{mn}(t).\) We get from the above,
So
Iterating Eq. (40) twice, we obtain
Rights and permissions
About this article
Cite this article
Gautam, K., Rawat, T.K., Parthasarathy, H. et al. Realization of commonly used quantum gates using perturbed harmonic oscillator. Quantum Inf Process 14, 3257–3277 (2015). https://doi.org/10.1007/s11128-015-1059-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11128-015-1059-0