Multi-party quantum private comparison with an almost-dishonest third party

Abstract

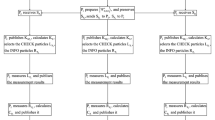
This article proposes the first multi-party quantum private comparison protocol with an almost-dishonest third party, where many participants can compare their secrets in either ascending or descending order without revealing any secret information to anyone. In order to do that, the participants need not to pre-share any secret key between them. As a consequence, the proposed scheme can be enforced in several environments such as multi-party ranking and multi-data ranking protocol.

Appendices

Appendix 1

$$\begin{aligned}&\frac{1}{\sqrt{d}}\sum \limits _{p=0}^{d-1} {\left| {pp\ldots p} \right\rangle _{n}}\\&\quad =\frac{1}{\sqrt{d}}\sum \limits _{p=0}^{d-1} \left( \frac{1}{\sqrt{d}}\sum \limits _{k_{1}=0}^{d-1} {e^{\frac{2\pi ipk_{1}}{d}}} F\left| {k_{1}} \right\rangle \otimes \frac{1}{\sqrt{d}}\sum \limits _{k_{2}=0}^{d-1} {e^{\frac{2\pi ipk_{2}}{d}}}F\left| {k_{2}} \right\rangle \otimes \cdots \otimes \frac{1}{\sqrt{d}}\sum \limits _{k_{n}=0}^{d-1} {e^{\frac{2\pi ipk_{n}}{d}}}F\left| {k_{n}} \right\rangle \right) \\&\quad =\frac{1}{\sqrt{d^{n+1}}}\sum \limits _{k_{1},k_{2}, \ldots ,k_{n}=0}^{d-1}{\sum \limits _{p=0}^{d-1} {\left( {e^{\frac{2\pi ipk_{1}}{d}}F\left| {k_{1}}\right\rangle \otimes e^{\frac{2\pi ipk_{2}}{d}}F\left| {k_{2}}\right\rangle \otimes \cdots \otimes e^{\frac{2\pi ipk_{n}}{d}}F\left| {k_{n}} \right\rangle }\right) }}\\&\quad =\frac{1}{\sqrt{d^{n+1}}}\sum \limits _{k_{1},k_{2}, \ldots ,k_{n}=0}^{d-1}{\sum \limits _{p=0}^{d-1} {e^{\frac{2\pi i\left( {pk_{1}+pk_{2}+\cdots +pk_{n}}\right) }{d}}}} \left( {F\left| {k_{1}} \right\rangle \otimes F\left| {k_{2}} \right\rangle \otimes \cdots \otimes F\left| {k_{n}} \right\rangle }\right) \\&\quad =\frac{1}{\sqrt{d^{n+1}}}\sum \limits _{k_{1},k_{2}, \ldots ,k_{n}=0}^{d-1}{\sum \limits _{p=0}^{d-1} {e^{\frac{2\pi ip\left( {k_{1}+k_{2}+\cdots +k_{n}}\right) }{d}}}} \left( {F\left| {k_{1}} \right\rangle \otimes F\left| {k_{2}} \right\rangle \otimes \cdots \otimes F\left| {k_{n}} \right\rangle }\right) \\&\quad =\frac{1}{\sqrt{d}}\sum \limits _{k_{1}\oplus k_{2}\oplus \cdots \oplus k_{n}=0} {F\left| {k_{1}} \right\rangle \otimes F\left| {k_{2}} \right\rangle \otimes \cdots \otimes F\left| {k_{n}} \right\rangle }\\&\frac{1}{\sqrt{2^{-1}d}}\sum \limits _{q=0}^{\frac{d}{2}-1} {\left| {qq\ldots q}\right\rangle _{n}} \\&\quad =\frac{1}{\sqrt{2^{-1}d}}\sum \limits _{q=0}^{\frac{d}{2}-1} {\left( {\frac{1}{\sqrt{d}}\sum \limits _{k_{1}=0}^{d-1} {e^{\frac{2\pi iqk_{1}}{d}}} F\left| {k_{1}} \right\rangle \otimes \frac{1}{\sqrt{d}}\sum \limits _{k_{2}=0}^{d-1} {e^{\frac{2\pi iqk_{2}}{d}}}F\left| {k_{2}} \right\rangle \otimes \cdots \otimes \frac{1}{\sqrt{d}}\sum \limits _{k_{n}=0}^{d-1} {e^{\frac{2\pi iqk_{n}}{d}}}F\left| {k_{n}} \right\rangle }\right) } \\&\quad =\frac{1}{\sqrt{2^{-1}d^{n+1}}}\sum \limits _{k_{1},k_{2}, \ldots ,k_{n}=0}^{d-1}{\sum \limits _{q=0}^{\frac{d}{2}-1} {\left( {e^{\frac{2\pi iqk_{1}}{d}}F\left| {k_{1}} \right\rangle \otimes e^{\frac{2\pi iqk_{2}}{d}}F\left| {k_{2}} \right\rangle \otimes \cdots \otimes e^{\frac{2\pi iqk_{n}}{d}}F\left| {k_{n}} \right\rangle }\right) }}\\&\quad =\frac{1}{\sqrt{2^{-1}d^{n+1}}}\sum \limits _{k_{1},k_{2}, \ldots ,k_{n}=0}^{d-1}{\sum \limits _{q=0}^{\frac{d}{2}-1} {e^{\frac{2\pi i\left( {qk_{1}+qk_{2}+\cdots +qk_{n}}\right) }{d}}}} \left( {F\left| {k_{1}} \right\rangle \otimes F\left| {k_{2}} \right\rangle \otimes \cdots \otimes F\left| {k_{n}} \right\rangle }\right) \\&\quad =\frac{1}{\sqrt{2^{-1}d^{n+1}}}\sum \limits _{k_{1},k_{2},\ldots ,k_{n}=0}^{d-1} {\sum \limits _{q=0}^{\frac{d}{2}-1} {e^{\frac{2\pi iq\left( {k_{1}+k_{2}+\cdots +k_{n}}\right) }{d}}}} \left( {F\left| {k_{1}} \right\rangle \otimes F\left| {k_{2}} \right\rangle \otimes \cdots \otimes F\left| {k_{n}} \right\rangle }\right) \\&\quad =\frac{1}{\sqrt{2^{-1}d}}\sum \limits _{k} {e^{\frac{2\pi iq\left( {k_{1}+k_{2}+\cdots +k_{n}}\right) }{d}}F\left| {k_{1}} \right\rangle \otimes F\left| {k_{2}} \right\rangle \otimes \cdots \otimes F\left| {k_{n}} \right\rangle } \end{aligned}$$

$(k~\hbox {satisfies}~k_{1}\oplus k_{2}\oplus \cdots \oplus k_{n}\ne 0\left( {\hbox {mod}~2}\right) ~\hbox {or}~k_{1}\oplus k_{2}\oplus \cdots \oplus k_{n}=0\left( {\hbox {mod}~d}\right) )$

Appendix 2

Theorem 1

The proposed scheme adequately performs the comparison of size relation.

Proof

In our proposed protocol, let $s_{i}$ be the secret of participant i and $\left| {p_{i}}\rangle \right.$, $\left| {q_{i}} \rangle \right.$ be two initial states that the TP sends to the participant i. Now, we further consider that $\left\{ {s_{i}} \right\} _{\max }$ be the maximum size of the secret $s_{i}$, where $l=\left\{ {s_{i}} \right\} _{\max } +1$, $d=2\,*\,l,$ and $\left| {q_{i}^{{\prime }{\prime }}} \rangle \right.$ denotes the qubit of the participant i that he/she sends to TP. Now, we demonstrate that how the proposed scheme performs the comparison of size relation.

$$\begin{aligned}&\left| {q_{i}^{{\prime }{\prime }}}\rangle \right. =\mathop {\prod }\nolimits _{s_{i}\oplus p_{i}} \left| {q_{i}}\rangle \right. =\left| {s_{i}+p_{i}+q_{i}\left( {\hbox {mod}~d}\right) } \right. \\&\hbox {If}~k=p_{i}+q_{i}\left( {\hbox {mod}~d}\right) \\&\hbox { then }k+s_{i}\in k\sim k+l-1\left( {\hbox {mod}~d}\right) \\&\exists ~\hbox {area:}\left\{ {k+l\sim k+2l-1\left( {\hbox {mod}~d}\right) } \right\} \, \hbox {must be empty}. \end{aligned}$$

Since the size relation of $k+s_{i}$ is equal to the size relation of $s_{i}$, therefore, we can constitute the size relation of $s_{i},$ using the non-empty area. In this way, the proposed scheme can perform the comparison of size relation. $\square$