Study of quantum correlation swapping with relative entropy methods

Abstract

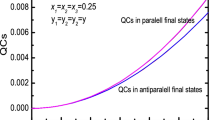
To generate long-distance shared quantum correlations (QCs) for information processing in future quantum networks, recently we proposed the concept of QC repeater and its kernel technique named QC swapping. Besides, we extensively studied the QC swapping between two simple QC resources (i.e., a pair of Werner states) with four different methods to quantify QCs (Xie et al. in Quantum Inf Process 14:653–679, 2015). In this paper, we continue to treat the same issue by employing other three different methods associated with relative entropies, i.e., the MPSVW method (Modi et al. in Phys Rev Lett 104:080501, 2010), the Zhang method (arXiv:1011.4333 [quant-ph]) and the RS method (Rulli and Sarandy in Phys Rev A 84:042109, 2011). We first derive analytic expressions of all QCs which occur during the swapping process and then reveal their properties about monotonicity and threshold. Importantly, we find that a long-distance shared QC can be generated from two short-distance ones via QC swapping indeed. In addition, we simply compare our present results with our previous ones.

Appendices

Appendix 1

Theorem

If two bipartite states can be converted mutually via single-partite unitary operations, then they are equivalent in the sense of calculating total, quantum and classical correlations with each of the three methods. To be specific, if $\rho _{ab} = u_a v_b \rho _{ab}' u_a^\dag v_b^\dag$, where u and v are unitary operators, then $T[\rho _{ab}] = T[\rho '_{ab}], D_\mathrm{M}[\rho _{ab}] = D_\mathrm{M}[\rho _{ab}'], C_\mathrm{M}[\rho _{ab}] = C_\mathrm{M}[\rho _{ab}'], D_\mathrm{Z}[\rho _{ab}] = D_\mathrm{Z}[\rho _{ab}'], C_\mathrm{Z}[\rho _{ab}] = C_\mathrm{Z}[\rho _{ab}'], D_\mathrm{R}[\rho _{ab}] = D_\mathrm{R}[\rho _{ab}']$, and $C_\mathrm{R}[\rho _{ab}] = C_\mathrm{R}[\rho _{ab}']$.

Proof

For a bipartite state, its product state is determined. Hence, its total correlations estimated in the three methods are equal to each other according to the definition. Since $\rho _{ab} = u_a v_b \rho _{ab}' u_a^\dag v_b^\dag$, in terms of Eqs. (5), (10) and (1) as well as the trace property of von Neumann entropy one can derive

$$\begin{aligned} T [\rho _{ab}]= & {} T \left[ u_a v_b \rho _{ab}' u_a^\dag v_b^\dag \right] = S\left\{ \pi \left[ u_a v_b \rho _{ab}' u_a^\dag v_b^\dag \right] \right\} -S\left\{ u_a v_b \rho _{ab}' u_a^\dag v_b^\dag \right\} \nonumber \\= & {} S\left\{ tr_au_a v_b \rho _{ab}' u_a^\dag v_b^\dag \otimes tr_bu_a v_b \rho _{ab}' u_a^\dag v_b^\dag \right\} -S\{\rho '_{ab}\}\nonumber \\= & {} S\left\{ tr_a\rho '_{ab} \otimes tr_b \rho '_{ab} \right\} - S\{\rho '_{ab}\} = S\{\pi [\rho '_{ab}]\}-S\{\rho '_{ab}\}= T [\rho _{ab}']. \end{aligned}$$

(88)

In terms of the classical state definition given in Eq. (2) and Eqs. (30–32), one knows that, if $\chi [\rho _{ab}]$ is a classical state of $\rho _{ab}$, then $u_a^\dag v_b^\dag \chi [\rho _{ab}]v_b u_a$ is a classical state of $\rho '_{ab}$, and vice versa. That is to say,

$$\begin{aligned} \chi [\rho '_{ab}] = u_a^\dag v_b^\dag \chi [\rho _{ab}]v_b u_a, \ \ \chi [\rho _{ab}] = u_a v_b\chi [\rho '_{ab}] v_b^\dag u_a^\dag . \end{aligned}$$

(89)

Using the definition of quantum discord given by Eq. (11) and the equality above, one can get

$$\begin{aligned} D_\mathrm{M}[\rho _{ab}]= & {} = \min _{\chi [\rho '_{ab}]} \left\{ S\left\{ u_a v_b\chi [\rho '_{ab}] v_b^\dag u_a^\dag \right\} - S\{u_a v_b \rho _{ab}' u_a^\dag v_b^\dag )\right\} \nonumber \\= & {} \min _{\chi [\rho '_{ab}]} \left\{ S\{\chi [\rho _{ab}']\}- S\{\rho '_{ab})\right\} = D_\mathrm{M}[\rho '_{ab}]. \end{aligned}$$

(90)

Meanwhile, one can further obtain

$$\begin{aligned} \chi ^\mathrm{M} [\rho _{ab} ] = u_a v_b \chi ^\mathrm{M} [\rho _{ab}'] v_b^\dag u_a^\dag . \end{aligned}$$

(91)

According to the definition of classical correlation given by Eq. (12) in the MPSVW method, one is readily to have

$$\begin{aligned} C_\mathrm{M}[\rho _{ab}]= & {} S\left\{ \pi \left[ \chi ^M [ \rho _{ab} ]\right] \right\} - S\left\{ \chi ^M [ \rho _{ab} ]\right\} \nonumber \\= & {} S\left\{ \pi \left[ u_a v_b \chi ^\mathrm{M} [\rho _{ab}'] v_b^\dag u_a^\dag \right] \right\} - S\{u_a v_b \chi ^\mathrm{M} [\rho _{ab}'] v_b^\dag u_a^\dag \}\nonumber \\= & {} S\left\{ \pi \left[ \chi ^M [ \rho '_{ab} ]\right] \right\} - S\left\{ \chi ^M [ \rho '_{ab} ]\right\} = C_\mathrm{M}[\rho '_{ab}]. \end{aligned}$$

(92)

From Eq. (93), one can further get

$$\begin{aligned} \pi [\chi [\rho _{ab} ]] = u_a v_b\pi [ \chi [\rho _{ab}']] v_b^\dag u_a^\dag . \end{aligned}$$

(93)

Using the definition of the exact classical correlation given in Eq. (15), one can obtain

$$\begin{aligned} C_\mathrm{Z}[\rho _{ab}]= & {} \max _{\chi [\rho _{ab}]} \{S\{\pi [\chi [\rho _{ab}]]\}-S\{\chi [\rho _{ab}]\}\nonumber \\= & {} \max _{\chi [\rho '_{ab}]} \{S\{u_a v_b\pi [ \chi [\rho _{ab}']] v_b^\dag u_a^\dag \}-S\{u_a v_b\chi [\rho '_{ab}] v_b^\dag u_a^\dag \}\}\nonumber \\= & {} \max _{\chi [\rho '_{ab}]} \{S\{ \pi [ \chi [\rho _{ab}']] \}-S\{\chi [\rho '_{ab}] \} \} = C_\mathrm{Z}[\rho '_{ab}]. \end{aligned}$$

(94)

At the same time, one can arrive at

$$\begin{aligned} \chi ^\mathrm{Z} [\rho _{ab} ] = u_a v_b \chi ^\mathrm{Z} [\rho _{ab}'] v_b^\dag u_a^\dag . \end{aligned}$$

(95)

Utilizing Eqs. (16) and (99), one gets

$$\begin{aligned} D_\mathrm{Z}[\rho _{ab}]= & {} S\{\chi ^\mathrm{Z} [\rho _{ab} ] \}- S\{\rho _{ab}\} =S\{ u_a v_b \chi ^\mathrm{Z} [\rho _{ab}'] v_b^\dag u_a^\dag \}- S\{\rho '_{ab}\} \nonumber \\= & {} S\{\chi ^\mathrm{Z} [\rho '_{ab} ] \}- S\{\rho '_{ab}\}= D_\mathrm{Z}[\rho '_{ab}]. \end{aligned}$$

(96)

As has been stressed in Eq. (19), $C_\mathrm{R}[\rho _{ab}]$ equals to $C_\mathrm{Z}[\rho _{ab}]$. Hence, according to $C_\mathrm{Z}[\rho _{ab}] = C_\mathrm{Z}[\rho _{ab}']$, one can directly get $C_\mathrm{R}[\rho _{ab}] = C_\mathrm{R}[\rho _{ab}']$. Moreover, according to the definition in Eq. (20), one obtains

$$\begin{aligned} Q_\mathrm{R}[\rho _{ab}]= T [\rho _{ab}]-C_\mathrm{R}[\rho _{ab}]= T [\rho _{ab}']-C_\mathrm{R}[\rho _{ab}']=Q_\mathrm{R}[\rho _{ab}']. \end{aligned}$$

(97)

$\square$

Corollary

In the case of $\rho _{ab} = u_a v_b \rho _{ab}' u_a^\dag v_b^\dag$ with u and v being unitary operators, $L_\mathrm{M}[\rho _{ab}] = L_\mathrm{M}[\rho _{ab}']$ and $L_\mathrm{Z}[\rho _{ab}] = L_\mathrm{Z}[\rho _{ab}']$.

Proof

Using $T[\rho _{ab}] = T[\rho '_{ab}], D_\mathrm{M}[\rho _{ab}] = D_\mathrm{M}[\rho _{ab}']$ and $C_\mathrm{M}[\rho _{ab}] = C_\mathrm{M}[\rho _{ab}']$ as well as the additivity relation given in Eq. (14), one can easily get $L_\mathrm{M}[\rho _{ab}] = L_\mathrm{M}[\rho _{ab}']$. Similarly, in terms of $T[\rho _{ab}] = T[\rho '_{ab}], D_\mathrm{Z}[\rho _{ab}] = D_\mathrm{Z}[\rho _{ab}'], C_\mathrm{Z}[\rho _{ab}] = C_\mathrm{Z}[\rho _{ab}']$ and the additivity relation shown in Eq. (18) as well, one is readily to obtain $L_\mathrm{Z}[\rho _{ab}] = L_\mathrm{Z}[\rho _{ab}']$. $\square$

Appendix 2

Partial derivatives in Sect. 3.2 in MPSVW method.

$$\begin{aligned} \frac{\partial S\{\chi [{\rho _{yz}^e}]\} }{\partial \alpha _2}= & {} \ \{2[\mathcal {G}(f_3,f_2,\alpha _2){-}\mathcal {G}(f_1,f_0,\alpha _2)]\sin \alpha _1 \cos \alpha _1 \nonumber \\&+\, \sqrt{\eta (1-\eta )}\xi \zeta \sin {2\alpha _2}\cos {2\alpha _1}\cos \omega \} \left[ \log _2 p_{yz}^{(10)}-\log _2 p_{yz}^{(00)}\right] \nonumber \\&+ \, \{2[\mathcal {G}(f_2,f_3,\alpha _2)-\mathcal {G}(f_0,f_1,\alpha _2)]\sin \alpha _1 \cos \alpha _1 \nonumber \\&- \, \sqrt{\eta (1-\eta )}\xi \zeta \sin {2\alpha _2}\cos {2\alpha _1}\cos \omega \} \left[ \log _2 p_{yz}^{(11)}- \log _2 p_{yz}^{(10)}\right] , \end{aligned}$$

(98)

$$\begin{aligned} \frac{\partial S\{\chi [{\rho _{yz}^e}]\} }{\partial \alpha _2}= & {} \ \{2[\mathcal {G}(f_3,f_1,\alpha _1){-}\mathcal {G}(f_2,f_0,\alpha _1)]\sin \alpha _2 \cos \alpha _2 \nonumber \\&+\, \sqrt{\eta (1{-}\eta )}\xi \zeta \sin {2\alpha _1}\cos {2\alpha _2}\cos \omega \} \left[ \log _2 p_{yz}^{(01)}{-}\log _2 p_{yz}^{(00)}\right] \nonumber \\&+\, \{2[\mathcal {G}(f_1,f_3,\alpha _1){-}\mathcal {G}(f_0,f_2,\alpha _1)]\sin \alpha _2 \cos \alpha _2 \nonumber \\&-\, \sqrt{\eta (1{-}\eta )}\xi \zeta \sin {2\alpha _1}\cos {2\alpha _2}\cos \omega \} \left[ \log _2 p_{yz}^{(11)}{-} \log _2 p_{yz}^{(10)}\right] ,\end{aligned}$$

(99)

$$\begin{aligned} \frac{\partial S\{\chi [{\rho _{yz}^e}]\} }{\partial \omega }= & {} \ \frac{1}{2}\sqrt{\eta (1-\eta )}\xi \zeta \sin {2\alpha _1}\sin {2\alpha _2}\sin \omega \nonumber \\&\times \, \left[ \log _2 p_{yz}^{(00)}+\log _2 p_{yz}^{(11)}-\log _2 p_{yz}^{(01)} -\log _2 p_{yz}^{(10)} \right] . \end{aligned}$$

(100)

If $(\alpha _1, \alpha _2, \omega )=(0,0,0)$ or $(\frac{\pi }{4},\frac{\pi }{4},0)$, then $\frac{\partial S\{\chi [{\rho _{yz}^e}]\} }{\partial \alpha _2}=0, \frac{\partial S\{\chi [{\rho _{yz}^e}]\} }{\partial \alpha _2}=0$ and $\frac{\partial S\{\chi [{\rho _{yz}^e}]\} }{\partial \omega }=0$.

Appendix 3

Partial derivatives in Sect. 3.2 in Zhang method.

$$\begin{aligned} \frac{\partial \mathcal {C}}{\partial \alpha _1}= & {} \ -\frac{1}{2} \sin \alpha _1 \cos \alpha _1 (f_{23}-f_{01})\left[ \log _2 \left( p_{yz}^{(00)}+p_{yz}^{(01)}\right) -\log _2\left( p_{yz}^{(10)}+p_{yz}^{(11)}\right) \right] \nonumber \\&- \ \{2[\mathcal {G}(f_3,f_2,\alpha _2)-\mathcal {G}(f_1,f_0,\alpha _2)]\sin \alpha _1 \cos \alpha _1 \nonumber \\&+\ \sqrt{\eta (1-\eta )}\xi \zeta \sin {2\alpha _2}\cos {2\alpha _1}\cos \omega \} \left[ \log _2 p_{yz}^{(10)}-\log _2 p_{yz}^{(00)}\right] \nonumber \\&-\ \{2[\mathcal {G}(f_2,f_3,\alpha _2)-\mathcal {G}(f_0,f_1,\alpha _2)]\sin \alpha _1 \cos \alpha _1 \nonumber \\&-\ \sqrt{\eta (1-\eta )}\xi \zeta \sin {2\alpha _2}\cos {2\alpha _1}\cos \omega \} \left[ \log _2 p_{yz}^{(11)}- \log _2 p_{yz}^{(10)}\right] ,\end{aligned}$$

(101)

$$\begin{aligned} \frac{\partial \mathcal {C}}{\partial \alpha _2}= & {} \ -\frac{1}{2} \sin \alpha _1 \cos \alpha _1 (f_{23}-f_{01})\left[ \log _2 (p_{yz}^{(00)}+p_{yz}^{(10)}) -\log _2(p_{yz}^{(01)}+p_{yz}^{(11)}) \right] \nonumber \\&-\ \{2[\mathcal {G}(f_3,f_1,\alpha _1)-\mathcal {G}(f_2,f_0,\alpha _1)]\sin \alpha _2 \cos \alpha _2 \nonumber \\&+\ \sqrt{\eta (1-\eta )}\xi \zeta \sin {2\alpha _1}\cos {2\alpha _2}\cos \omega \} \left[ \log _2 p_{yz}^{(01)}-\log _2 p_{yz}^{(00)}\right] \nonumber \\&-\ \{2[\mathcal {G}(f_1,f_3,\alpha _1)-\mathcal {G}(f_0,f_2,\alpha _1)]\sin \alpha _2 \cos \alpha _2 \nonumber \\&-\ \sqrt{\eta (1-\eta )}\xi \zeta \sin {2\alpha _1}\cos {2\alpha _2}\cos \omega \} \left[ \log _2 p_{yz}^{(11)}- \log _2 p_{yz}^{(10)}\right] ,\end{aligned}$$

(102)

$$\begin{aligned} \frac{\partial \mathcal {C}}{\partial \omega }= & {} \ -\frac{1}{2}\sqrt{\eta (1-\eta )}\xi \zeta \sin {2\alpha _1}\sin {2\alpha _2}\sin \omega \nonumber \\&\times \ \left[ \log _2 p_{yz}^{(00)}+\log _2 p_{yz}^{(11)}-\log _2 p_{yz}^{(01)} -\log _2 p_{yz}^{(10)} \right] . \end{aligned}$$

(103)

Obviously, $\frac{\partial \mathcal {C}}{\partial \alpha _1}=\frac{\partial }{\partial \alpha _2}=\frac{\partial \mathcal {C}}{\partial \omega }=0$ in the case that $(\alpha _1, \alpha _2, \omega )=(0,0,0)$ or $(\frac{\pi }{4},\frac{\pi }{4},0)$.

Appendix 4

Explanation of quantity $L_Z[\rho _{ab}]$.

According to Eqs. (8) and (17), one can get

$$\begin{aligned} L_Z[\rho _{ab}]= S\{\pi [\chi ^Z[\rho _{ab}]]\}-S\{\pi [\rho _{ab}]\}. \end{aligned}$$

(104)

Since $S\{\pi [\chi ^Z[\rho _{ab}]]\}$ and $S\{\pi [\rho _{ab}]\}$ can be expressed as

$$\begin{aligned} S\{\pi [\chi ^Z[\rho _{ab}]]\}= & {} S\{tr_b[\pi [\chi ^Z[\rho _{ab}]]]\}+S\{tr_a[\pi [\chi ^Z[\rho _{ab}]]]\},\end{aligned}$$

(105)

$$\begin{aligned} S\{\pi [\rho _{ab}]\}= & {} S\{tr_b[\pi [\rho _{ab}]]\}+S\{tr_a[\pi [\rho _{ab}]], \end{aligned}$$

(106)

combining Eqs. (108) and (109), one can get

$$\begin{aligned} L_Z[\rho _{ab}]= & {} S\{tr_b[\pi [\chi ^Z[\rho _{ab}]]]\}-S\{tr_b[\pi [\rho _{ab}]]\}\nonumber \\&+S\{tr_a[\pi [\chi ^Z[\rho _{ab}]]]\}-S\{tr_a[\pi [\rho _{ab}]]\}. \end{aligned}$$

(107)

Further, let

$$\begin{aligned}&L_a^Z \equiv S\{tr_b[\pi [\chi ^Z[\rho _{ab}]]]\}-S\{tr_b[\pi [\rho _{ab}]]\},\end{aligned}$$

(108)

$$\begin{aligned}&L_b^Z \equiv S\{tr_a[\pi [\chi ^Z[\rho _{ab}]]]\}-S\{tr_a[\pi [\rho _{ab}]]\}, \end{aligned}$$

(109)

easily one can see that $L_a^Z$ actually denotes the uncertainty information in the particle a associated with the appropriate classical state $\chi ^Z[\rho _{ab}]$ and $L_b^Z$ represents that in the particle b. In this situation, for the bipartite quantum state $\rho _{ab}$, the quantity

$$\begin{aligned} L_Z[\rho _{ab}]= L_a^Z + L_b^Z \end{aligned}$$

(110)

just represents the sum of uncertainty information of single particle a and that of b.