Real-time simulation of H–P noisy Schrödinger equation and Belavkin filter

Abstract

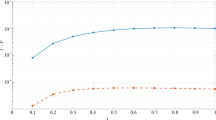
The Hudson–Parthasarathy noisy Schrödinger equation is an infinite-dimensional differential equation where the noise operators—Creation, Annihilation and Conservation processes—take values in Boson Fock space. We choose a finite truncated basis of exponential vectors for the Boson Fock space and obtained the unitary evolution in a truncated orthonormal basis using the Gram–Schmidt orthonormalization process to the exponential vectors. Then, this unitary evolution is used to obtained the approximate evolution of the system state by tracing out over the bath space. This approximate evolution is compared to the exact Gorini–Kossakowski–Sudarshan–Lindblad equation for the system state. We also perform a computation of the rate of change of the Von Neumann entropy for the system assuming vacuum noise state and derive condition for entropy increase. Finally, by taking non-demolition measurement in the sense of Belavkin, we simulate the Belavkin quantum filter and show that the Frobenius norm of the error observables $j_t(X)-\pi _t(X)$ becomes smaller with time for a class of observable X. Here $j_t(X)$ is the H–P equation observable and $\pi _t(X)$ is the Belavkin filter output observable. In last, we have derived an approximate expression for the filtered density and entropy of the system after filtering.