Abstract
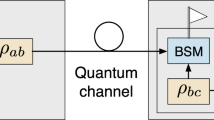
In this paper, a model for single photon amplification based on cluster-state quantum computation is proposed. A rescaling of the probability amplitudes of a deteriorated qubit in favor of the one-photon component will define the amplifier’s gain. Unlike the heralded quantum amplifiers, the probabilistic success of the whole process will not depend on the successful detection of a heralding signal. Instead, the whole procedure will rely upon a single-qubit measurement, which is simpler compared to any two-qubit interaction gate in the heralded quantum amplifiers. The proposed model can be used as a qubit protector against propagation losses in long-distance quantum communication networks.















Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
This requirement is specific to our analysis, where in general the transfer matrix is Hermitian.
Where \(\vert {\psi }\rangle \) = \(\alpha \vert {0}\rangle +\beta \vert {1}\rangle \) is an arbitrary qubit state.
The \(\frac{1}{\sqrt{2}}\)factor will be taken care of when normalizing the whole state.
This indistinguishability is crucial to the whole amplification process.
Since the detection of one photon in either \(\hat{d_{+}}\) or \(\hat{d_{-}}\) leads to Eq. 7, the probability to successfully produce that state is given by twice its norm.
All of the probability amplitudes can be adjusted as a function of the linear optical elements that will be used during experimentation. This will be clear in Sect. 3.
\(\vert {+}\rangle \) and \(\vert {-}\rangle \) are the eigenstates of the Pauli-X operator with eigenvalues +1, −1, respectively.
The Pauli group is the group of the famous Pauli \(\sigma \) operators.
Where X is the Pauli \(\sigma _{x}, \sigma _{x} \vert {+}\rangle =\vert {+}\rangle \).
\(\rho ^{\prime }={U}\rho {U^{\dagger }}\).
Where this step to be included in the ‘polarization encoding’ block in our diagrams from now on.
This simple encoder consists of: an input in a general polarization state to be encoded, a PBS and an entanglement resource in the state \(\vert {\phi ^{+}}\rangle \). At the PBS, the general input state will be mixed with one member of the entangled resource, and then the detection of exactly one photon at the output of the PBS means that the other two are exiting the device.
Again this can be put in the standard form by applying a Hadamard to qubits 1 and 4.
References
Preskill, J.: Physics 219. Lecture notes. http://www.theory.caltech.edu/people/preskill/ph229/
Caves, C.M.: Quantum limits on noise in linear amplifiers. Phys. Rev. D 26, 1817 (1982)
Wootters, W.K., Zurek, W.H.: A single quantum cannot be cloned. Nature 299, 802–803 (1982)
Ralph, T.C., Lund, A.P.: Nondeterministic noiseless linear amplification of quantum systems. In: Lvovsky, A. (eds.) Quantum Communication Measurement and Computing Proceedings of 9th International Conference, pp. 155–160 (2009)
Osorio, C.I., Bruno, N., Sangouard, N., Zbinden, H., Gisin, N., Thew, R.T.: Heralded photon amplification for quantum communication. Phys. Rev. A 86, 023815 (2012)
Jeffers, J.: Nondeterministic amplifier for two-photon superpositions. Phys. Rev. A 82, 063828 (2010)
Meyer-Scott, E., Bula, M., Bartkiewicz, K., Ĉernoch, A., Soubusta, J., Jennewein, T., Lemr, K.: Entanglement-based linear-optical qubit amplifier. Phys. Rev. A 88, 012327 (2013)
Knill, E., Laflamme, R., Milburn, G.J.: A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001)
Raussendorf, R., Briegel, H.J.: A one-way quantum computer. Phys. Rev. Lett. 86, 5188 (2001)
Browne, D.E., Briegel, H. J.: One-way quantum computation—a tutorial introduction. arXiv:quant-ph/0603226
Nielsen, M. A.: Cluster-state quantum computation. arXiv:quant-ph/0504097
Nielsen, M.A., Chuang, I.L.: Quantum computation and quantum information, 1st edn. Cambridge University Press, Cambridge (2000)
Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009)
Bennett, C.H., Brassard, G., Mermin, N.D.: Quantum cryptography without Bells theorem. Phys. Rev. Lett. 68, 557 (1992)
Ekert, A.K.: Quantum cryptography based on Bells theorem. Phys. Rev. Lett. 67, 661 (1991)
Zbinden, H., Bechmann-Pasquinucci, H., Gisin, N., Ribordy, G.: Quantum cryptography. Appl. Phys. B 67, 743748 (1998)
Gisin, N., Ribordy, G., Tittel, W., Zbinden, H.: Quantum cryptography. Rev. Mod. Phys. 74, 145 (2002)
Bennett, C.H., Brassard, G., Crpeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 70, 1895 (1993)
Bouwmeester, D., Pan, J.-W., Mattle, K., Eibl, M., Weinfurter, H., Zeilinger, A.: Experimental quantum teleportation. Nature 390, 575–579 (1997)
Duan, L.-M., Lukin, M.D., Cirac, J.I., Zoller, P.: Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001)
Sangouard, N., Simon, C., de Riedmatten, H., Gisin, N.: Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33 (2011)
Azuma, K., Tamaki, K., Lo, H.-K.: All-photonic quantum repeaters. Nat. Commun. 6, Article number: 6787 (2015)
Gerry, C., Knight, P.: Introductory Quantum Optics, Chapter 6, 1st edn. Cambridge University Press, Cambridge (2005)
Barnum, H., Nielsen, M.A., Schumacher, B.: Information transmission through a noisy quantum channel. Phys. Rev. A 57, 4153 (1997)
Gupta, V.P., Mandayam, P., Sunder, V.S.: The Functional Analysis of Quantum Information Theory. Springer, Berlin (2015)
Christensen, O.: Functions, Spaces, and Expansions. Birkhuser Mathematics, Basel (2010)
Desurvire, E.: A three-dimensional quantum vacuum-noise/signal beamsplitter model for nonideal linear optical amplifiers. Opt. Fiber Technol. 5(1), 81 (1999)
Ketterle, W.: 8.422 Atomic and Optical Physics II, Spring 2013 (Massachusetts Institute of Technology: MIT OpenCourseWare). http://ocw.mit.edu/courses/physics/8-422-atomic-and-optical-physics-ii-spring-2013/
Lambropoulos, P., Petrosyan, D.: Fundamentals of Quantum Optics and Quantum Information. Springer, Berlin (2007)
Agarwal, G.S.: Quantum Optics, Chapter 10, 1st edn. Cambridge University Press, Cambridge (2012)
Deutsch, I.H.: Physics 581 Quantum Optics II. http://info.phys.unm.edu/~ideutsch/Classes/Phys581F16/index.htm
Eastin, B., Flammia, S.T.: Q-circuit tutorial. arXiv:quant-ph/0406003v2 (This diagram was plotted using this tool)
Kok, P., Lovett, B.W.: Introduction to Optical Quantum Information Processing. Cambridge University Press, Cambridge (2010)
Gottesman, D.: The Heisenberg Representation of Quantum Computers. arXiv:quant-ph/9807006
Gottesman, D.: Stabilizer Codes and Quantum Error Correction. arXiv:quant-ph/9705052
Korzh, B., et al.: Provably secure and practical quantum key distribution over 307 km of optical fibre. Nat. Photon. 9, 163168 (2015)
Jozsa, R.: Fidelity for mixed quantum states. J. Mod. Opt. 41(12), 2315–2323 (1994)
Gottesman, D.: Quantum Error Correction QECC2007. Course http://perimeterinstitute.ca/personal/dgottesman/QECC2007/
Vazirani, U.: CS294-2: quantum computation. Lecture notes. https://people.eecs.berkeley.edu/~vazirani/s09quantum.html
Chao-Yang, L., Zhou, X.-Q., Ghne, O., Gao, W.-B., Zhang, J., Yuan, Z.-S., Goebe, A., Yang, T., Pan, J.-W.: Experimental entanglement of six photons in graph states. Nat. Phys. 3, 91–95 (2007)
Browne, D.E., Rudolph, T.: Resource-efficient linear optical quantum computation. Phys. Rev. Lett. 95, 010501 (2005)
Pittman, T.B., Jacobs, B.C., Franson, J.D.: Probabilistic Quantum Encoder for Single-Photon Qubits. arXiv:quant-ph/0312097
Walther, P., Resch, K.J., Rudolph, T., Schenck, E., Weinfurter, H., Vedral, V., Aspelmeyer, M., Zeilinger, A.: Experimental one-way quantum computing. Nature 434, 169–176 (2005)
Shannon, C.E.: A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423, 623–656 (1948)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Elemy, H. A one-way quantum amplifier for long-distance quantum communication. Quantum Inf Process 16, 134 (2017). https://doi.org/10.1007/s11128-017-1582-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-017-1582-2