Skip to main content
Springer Nature Link
Log in

Quantum-memory-assisted entropic uncertainty relations under weak measurements

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

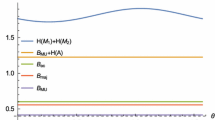
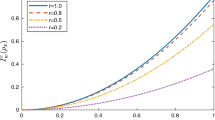
We investigate quantum-memory-assisted entropic uncertainty relations (EURs) based on weak measurements. It is shown that the lower bound of EUR revealed by weak measurements is always larger than that revealed by the corresponding projective measurements. A series of lower bounds of EUR under both weak measurements and projective measurements are presented. Interestingly, the quantum-memory-assisted EUR based on weak measurements is a monotonically decreasing function of the strength parameter. Furthermore, some information-theoretic inequalities associated with weak measurements are also derived.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Heisenberg, W.: Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 43, 172 (1927). English translation in: Wheeler, J.A., Zurek, W.H. (eds.) Quantum Theory and Measurement, pp. 62–84. Princeton University Press, Princeton (1983)

  2. Robertson, H.P.: The uncertainty principle. Phys. Rev. 34, 163 (1929)

    Article  ADS  Google Scholar 

  3. Deutsch, D.: Uncertainty in quantum measurements. Phys. Rev. Lett. 50, 631 (1983)

    Article  ADS  MathSciNet  Google Scholar 

  4. Maassen, H., Uffink, J.B.M.: Generalized entropic uncertainty relations. Phys. Rev. Lett. 60, 1103 (1988)

    Article  ADS  MathSciNet  Google Scholar 

  5. Tomamichel, M., Renner, R.: Uncertainty relation for smooth entropies. Phys. Rev. Lett. 106, 110506 (2011)

    Article  ADS  Google Scholar 

  6. Birula, I.B.: Formulation of the uncertainty relations in terms of the Rényi entropies. Phys. Rev. A 74, 052101 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  7. Zozor, S., Vignat, C.: On classes of non-Gaussian asymptotic minimizers in entropic uncertainty principles. Phys. A 375, 499 (2007)

    Article  Google Scholar 

  8. Bosyk, G.M., Portesi, M., Plastino, A.: Collision entropy and optimal uncertainty. Phys. Rev. A 85, 012108 (2012)

    Article  ADS  Google Scholar 

  9. Luis, A.: Effect of fluctuation measures on the uncertainty relations between two observables: different measures lead to opposite conclusions. Phys. Rev. A 84, 034101 (2011)

    Article  ADS  Google Scholar 

  10. Wilk, G., Wlodarczyk, Z.: Uncertainty relations in terms of the Tsallis entropy. Phys. Rev. A 79, 062108 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  11. Birula, I.B., Rudnicki, L.: Comment on “Uncertainty relations in terms of the Tsallis entropy”. Phys. Rev. A 81, 026101 (2010)

    Article  ADS  Google Scholar 

  12. Wehner, S., Winter, A.: Entropic uncertainty relations—a survey. New. J. Phys. 12, 025009 (2010)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. Berta, M., Chrisandl, M., Colbeck, R., Renes, J.M., Renner, R.: The uncertainty principle in the presence of quantum memory. Nat. Phys. 6, 659 (2010)

    Article  Google Scholar 

  14. Renes, J.M., Boileau, J.C.: Conjectured strong complementary information tradeoff. Phys. Rev. Lett. 103, 020402 (2009)

    Article  ADS  Google Scholar 

  15. Coles, P.J., Yu, L., Gheorghiu, V., Griffiths, R.B.: Information-theoretic treatment of tripartite systems and quantum channels. Phys. Rev. A 83, 062338 (2011)

    Article  ADS  Google Scholar 

  16. Krishna, M., Parthasarathy, K.R.: An entropic uncertainty principle for quantum measurements. Sankhya Indian J. Stat. Ser. A 64, 842 (2002)

    MathSciNet  MATH  Google Scholar 

  17. Pati, A.K., Wilde, M.M., Devi, A.R.U., Rajagopal, A.K.: Quantum discord and classical correlation can tighten the uncertainty principle in the presence of quantum memory. Sudha Phys. Rev. A 86, 042105 (2012)

    Article  ADS  Google Scholar 

  18. Ollivier, H., Zurek, W.H.: Quantum discord: a measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001)

    Article  ADS  MATH  Google Scholar 

  19. Henderson, L., Vedral, V.: Classical, quantum and total correlations. J. Phys. A Math. Theor. 34, 6899 (2001)

    ADS  MathSciNet  MATH  Google Scholar 

  20. Modi, K., et al.: The classical-quantum boundary for correlations: discord and related measures. Rev. Mod. Phys. 84, 1655 (2012)

    Article  ADS  Google Scholar 

  21. Aharonov, Y., Albert, D.Z., Vaidman, L.: How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 60, 1351 (1988)

    Article  ADS  Google Scholar 

  22. Oreshkov, O., Brun, T.A.: Weak measurements are universal. Phys. Rev. Lett. 95, 110409 (2005)

    Article  ADS  Google Scholar 

  23. Hosten, O., Kwiat, P.: Observation of the spin Hall effect of light via weak measurements. Science 319, 787 (2008)

    Article  ADS  Google Scholar 

  24. Lundeen, J.S., et al.: Direct measurement of the quantum wavefunction. Nature 474, 188 (2011)

    Article  Google Scholar 

  25. Bernardo, B.D.L., Martins, W.S., Azevedo, S., Rosas, A.: Uncertainty control and precision enhancement of weak measurements in the quadratic regime. Phys. Rev. A 92, 012109 (2015)

  26. Parks, A.D., Gray, J.E.: Variance control in weak-value measurement pointers. Phys. Rev. A 84, 012116 (2011)

    Article  ADS  Google Scholar 

  27. Rozema, L.A., Darabi, A., Mahler, D.H., Hayat, A., Soudagar, Y., Steinberg, A.M.: Violation of Heisenberg’s measurement-disturbance relationship by weak measurements. Phys. Rev. Lett. 109, 100404 (2012)

    Article  ADS  Google Scholar 

  28. Singh, U., Pati, A.: Quantum discord with weak measurements. Ann. Phys. 343, 141 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  29. Coles, P. J., Yu, L., Zwolak, M. Relative entropy derivation of the uncertainty principle with quantum side information. arXiv:1105.4865

  30. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  31. Peres, A.: Neumark’s theorem and quantum inseparability. Found. Phys. 20, 1441 (1990)

    Article  ADS  MathSciNet  Google Scholar 

  32. Jozsa, R., koashi, M., Linden, N., Popescu, S., Presnell, S., Shepherd, D., Winter, A.: Entanglement cost of generalised measurements. arXiv:quant-ph/0303167

  33. Singh, U., Pati, A. Weak measurement induced super discord can resurrect lost quantumness. arXiv:1305.4393

  34. Han, W., et al.: Enhancing entanglement trapping by weak measurement and quantum measurement reversal. arXiv:1309.6759

  35. Wang, Y.K., et al.: Super-quantum correlation and geometry for Bell-diagonal states with weak measurements. Quantum Inf. Process. 13, 283 (2014)

    Article  MATH  Google Scholar 

  36. Li, B., Chen, L., Fan, H.: Non-zero total correlation means non-zero quantum correlation. Phys. Lett. A 378, 1249 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This research was supported by the grants from the Natural Science Foundation of China (11571220) and (11105226); the Natrual Science Foundation of Shandong Province (ZR2016AM23); the Fundamental Research Funds for the Central Universities Nos. (15CX02075A) and (15CX05062A); Macao Science and Technology Development Fund No. (003/2015/A1).

Author information

Authors and Affiliations

  1. Department of Mathematics, Shanghai University, Shanghai, 200444, People’s Republic of China

    Lei Li & Qing-Wen Wang

  2. College of Science, China University of Petroleum, Qingdao, 266580, People’s Republic of China

    Lei Li, Shu-Qian Shen & Ming Li

Authors
  1. Lei Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Qing-Wen Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Shu-Qian Shen
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Ming Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Qing-Wen Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, L., Wang, QW., Shen, SQ. et al. Quantum-memory-assisted entropic uncertainty relations under weak measurements. Quantum Inf Process 16, 188 (2017). https://doi.org/10.1007/s11128-017-1638-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-017-1638-3

Keywords