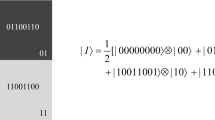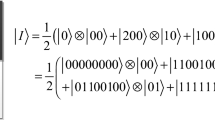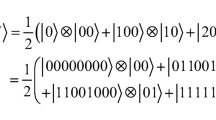Skip to main content
Springer Nature Link
Log in

Quantum watermarking scheme through Arnold scrambling and LSB steganography

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

Based on the NEQR of quantum images, a new quantum gray-scale image watermarking scheme is proposed through Arnold scrambling and least significant bit (LSB) steganography. The sizes of the carrier image and the watermark image are assumed to be \(2n\times 2n\) and \(n\times n\), respectively. Firstly, a classical \(n\times n\) sized watermark image with 8-bit gray scale is expanded to a \(2n\times 2n\) sized image with 2-bit gray scale. Secondly, through the module of PA-MOD N, the expanded watermark image is scrambled to a meaningless image by the Arnold transform. Then, the expanded scrambled image is embedded into the carrier image by the steganography method of LSB. Finally, the time complexity analysis is given. The simulation experiment results show that our quantum circuit has lower time complexity, and the proposed watermarking scheme is superior to others.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Feynman, R.: Simulating physics with computers. Int. J. Theor. Phys. 21(6–7), 467–488 (1982)

    Article  MathSciNet  Google Scholar 

  2. Deutsch, D.: Quantum theory, the church-turing principle and the universal quantum computer. Proc. R. Soc. Lond. A 400, 97–117 (1985)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  3. Shor, P.: Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings of the 35th Annual Symposium on Foundations of Computer Science, 124–134 (1994)

  4. Grover, L.A.: fast quantum mechanical algorithm for database search. In: Proceedings of the 28th Annual ACM Symposium on Theory of Computing, 212–219 (1996)

  5. Venegas-Andraca, S., Bose, S.: Storing, processing, and retrieving an image using quantum mechanics.In: Proceedings of SPIE Conference of Quantum Information and Computation, 5105, 134–147 (2003)

  6. Latorre, J.: Image Compression and Entanglement. arXiv:quant-ph/0510031 (2005)

  7. Le, P., Dong, F., Hirota, K.: A flexible representation of quantum images for polynomial preparation, image compression, and processing operations. Quant. Inf. Process. 10(1), 63–84 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  8. Zhang, Y., Lu, K., Gao, Y., et al.: NEQR: a novel enhanced quantum representation of digital images. Quant. Inf. Process. 12(8), 2833–2860 (2013)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  9. Zhang, Y., Lu, K., Gao, Y., Xu, K.: A novel quantum representation for log-polar images. Quant. Inf. Process. 12(9), 3103–3126 (2013)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  10. Li, H., Zhu, Q., Lan, S., Shen, C., Zhou, R., Mo, J.: Image storage, retrieval, compression and segmentation in a quantum system. Quant. Inf. Process. 12(6), 2269–2290 (2013)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  11. Li, H., Zhu, Q., Zhou, R., Song, L., Yang, X.: Multi-dimensional color image storage and retrieval for a normal arbitrary quantum superposition state. Quant. Inf. Process. 13(4), 991–1011 (2014)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  12. Yuan, S., Mao, X., Xue, Y., Chen, L., Xiong, Q., Compare, A.: SQR: a simple quantum representation of infrared images. Quant. Inf. Process. 13(6), 1353–1379 (2014)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  13. Sang, J., Wang, S., Li, Q.: A novel quantum representation of color digital images. Quant. Inf. Process 16(2), 42 (2017)

    Article  MathSciNet  ADS  Google Scholar 

  14. Iliyasu, A.: Towards realising secure and efficient image and video processing applications on quantum computers. Entropy 15, 2874–2974 (2013)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  15. Yan, F., Iliyasu, A.M., Venegas-Andraca, S.E.: A survey of quantum image representations. Quant. Inf. Process 15, 1–35 (2016)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  16. Yan, F.: Quantum Computation Based Image Data Searching, Image Watermarking, and representation of Emotion Space. Ph.D. Thesis, Tokyo Institute of Technology, Japan (2014)

  17. Yan, F., Iliyasu, A., Jiang, Z.: Quantum computation-based image representation, processing operations and their applications. Entropy 16(10), 5290–5338 (2014)

    Article  MathSciNet  ADS  Google Scholar 

  18. Le, P.Q., Iliyasu, A.M., Dong, F., et al.: Strategies for designing geometric transformations on quantum images. Theor. Comput. Sci. 412(15), 1406–1418 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  19. Fan, P., Zhou, R.G., Jing, N., et al.: Geometric transformations of multidimensional color images based on NASS. Inf. Sci. S 340–341, 191–208 (2016)

    Article  Google Scholar 

  20. Le, P.Q., Iliyasu, A.M., Dong, F., et al.: Fast geometric transformations on quantum images. Iaeng Int. J. Appl. Math. 40(3), 113–123 (2010)

    MathSciNet  MATH  Google Scholar 

  21. Le, P.Q., Iliyasu, A.M., Dong, F., et al.: Efficient color transformations on quantum images. J. Adv. Comput. Intell. Intell. Inf. 15(6), 698–706 (2011)

    Article  Google Scholar 

  22. Fan, P., Zhou, Rigui: Quantum gray-scale image translation transform. J. Comput. Inf. Syst. 11(23), 8763–8770 (2015)

    Google Scholar 

  23. Wang, J., Jiang, N., Wang, L.: Quantum image translation. Quant. Inf. Process. 14(5), 1589–1604 (2015)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  24. Zhou, R.G., Tan, C., Hou, I.: Global and local translation designs of quantum image based on FRQI. Int. J. Theor. Phys. 56(4), 1382–1398 (2017)

    Article  MathSciNet  Google Scholar 

  25. Sang, J., Wang, S., Niu, X.: Quantum realization of the nearest-neighbor interpolation method for FRQI and NEQR. Quant. Inf. Process. 15(1), 37–64 (2016)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  26. Jiang, N., Wang, L.: Quantum image scaling using nearest neighbor interpolation. Quant. Inf. Process. 14(5), 1559–1571 (2015)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  27. Jiang, N., Wang, J., Mu, Y.: Quantum image scaling up based on nearest-neighbor interpolation with integer scaling ratio. Quant. Inf. Process. 14(11), 4001–4026 (2015)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  28. Jiang, N., Wu, W.Y., Wang, L.: The quantum realization of Arnold and Fibonacci image scrambling. Quant. Inf. Process. 13(5), 1223–1236 (2014)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  29. Jiang, N., Wang, L.: Analysis and improvement of the quantum Arnold image scrambling. Quant. Inf. Process. 13(7), 1545–1551 (2014)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  30. Jiang, N., Wang, L., Wu, W.Y.: Quantum Hilbert image scrambling. Int. J. Theor. Phys. 53(7), 2463–2484 (2014)

    Article  MATH  Google Scholar 

  31. Zhou, RiGui, Sun, YaJuan, Fan, Ping: Quantum image Gray-code and bit-plane scrambling. Quant. Inf. Process. 14, 1717–1734 (2015)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  32. Sang, J., Wang, S., Shi, X., Li, Qiong: Quantum realization of Arnold scrambling for IFRQI. Int. J. Theor. Phys. 55(8), 3706–3721 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  33. Caraiman, S., Manta, V.I.: Image segmentation on a quantum computer. Quant. Inf. Process. 14(5), 1693–1715 (2015)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  34. Zhang, Y., Lu, K., Xu, K., et al.: Local feature point extraction for quantum images. Quant. Inf. Process. 14(5), 1573–1588 (2015)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  35. Zhang, Y., Lu, K., Gao, Y.H.: QSobel: a novel quantum image edge extraction algorithm. Sci. China Inf. Sci. 58(1), 1–13 (2015)

    MATH  Google Scholar 

  36. Jiang, N., Dang, Y., Wang, J.: Quantum image matching. Quant. Inf. Process. 15(9), 3543–3572 (2016)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  37. Zhang, W.W., Gao, F., Liu, B., Wen, Q.Y., Chen, H.: A watermark strategy for quantum images based on quantum Fourier transform. Quant. Inf. Process. 12(2), 793–803 (2013)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  38. Song, X.H., Wang, S., Liu, S., et al.: A dynamic watermarking scheme for quantum images using quantum wavelet transform. Quant. Inf. Process. 12(12), 3689–3706 (2013)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  39. Song, X., Wang, S., El-Latif, A.A.A., Niu, X.: Dynamic watermarking scheme for quantum images based on Hadamard transform. Multimed. Syst. 20(4), 379–388 (2014)

    Article  Google Scholar 

  40. Miyake, S., Nakamael, K.: A quantum watermarking scheme using simple and small-scale quantum circuits. Quant. Inf. Process. 15, 1849–1864 (2016)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  41. Heidari, S., Naseri, M.: A novel LSB based quantum watermarking. Int. J. Theor. Phys. 55(10), 1–14 (2016)

    Article  MATH  Google Scholar 

  42. Tirkel, A.Z., Rankin, G.A., VanSchyndel, R.M et al.: Electronic watermark. In: Proceedings of Digital Image Computing: Techniques and Applications, Macquarie University. 666–672 (1993)

  43. Arnold, V.I., Avez, A.: Ergodic Problems of Classical Mechanics. Benjamin, New York (1968)

    MATH  Google Scholar 

  44. Dyson, F.J., Falk, H.: Period of a discrete cat mapping. Am. Math. Mon. 99(7), 603–614 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  45. Islam, M.S., Rahman, M.M., Begum, Z., et al.: Low cost quantum realization of reversible multiplier circuit. Inf. Technol. J. 8(2), 208–213 (2009)

    Article  Google Scholar 

  46. Thapliyal, H., Ranganathan, N.A .: New design of the reversible subtractor circuit. In: 11th IEEE Conference on Nanotechnology (IEEE-NANO), 2011. IEEE. pp. 1430–1435 (2011)

  47. Kotiyal, S., Thapliyal, H., Ranganathan, N.: Circuit for reversible quantum multiplier based on binary tree optimizing ancilla and garbage bits. In: 2014 27th International Conference on VLSI Design and 2014 13th International Conference on Embedded Systems. IEEE. 545–550 (2014)

  48. Weinfurter, H., Smolin, J.A.: Elementary gates for quantum computation. Phys. Rev. A 52, 3457 (1995)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China under Grant No. 61463016, Program for New Century Excellent Talents in University under Grant No. NCET-13-0795, Training program of Academic and technical leaders of Jiangxi Province under Grant No. 20153BCB22002, and the advantages of scientific and technological innovation team of Nanchang City under Grant No. 2015CXTD003. Project of Science and Technology of Jiangxi province Grant No. 20161BAB202065. Project of International Cooperation and Exchanges of Jiangxi Province under Grant No. 20161BBH80034. Project of Humanities and Social Sciences in colleges and universities of Jiangxi Province under Grant No. JC161023.

Author information

Authors and Affiliations

  1. College of Information Engineering, Shanghai Maritime University, Shanghai, 201306, China

    Ri-Gui Zhou

  2. School of Information Engineering, East China Jiaotong University, Nanchang, 330013, Jiangxi, China

    Wenwen Hu & Ping Fan

Authors
  1. Ri-Gui Zhou
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Wenwen Hu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Ping Fan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ping Fan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, RG., Hu, W. & Fan, P. Quantum watermarking scheme through Arnold scrambling and LSB steganography. Quantum Inf Process 16, 212 (2017). https://doi.org/10.1007/s11128-017-1640-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-017-1640-9

Keywords