Skip to main content

Advertisement

Springer Nature Link
Log in

Quantum discord for two-qubit systems in the Bloch channel: effects of longitudinal and transversal relaxation times

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

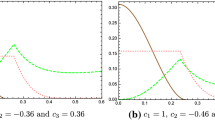
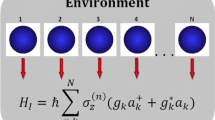
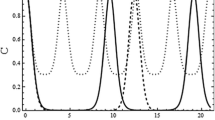
Quantum discord is studied for two-qubit systems with different settings under the influence of the Bloch channel which is characterized by the longitudinal and transversal relaxation times and the environmental temperature. The relaxation of the quantum discord strongly depends on the ratio of the two relaxation times and the environmental temperature. It is found that the ratio of the quantum discord to the total correlation becomes finite or zero asymptotically, depending on the ratio of the relaxation times and the system setting. Furthermore, the optimal setting for sharing the quantum discord is discussed for given environmental temperature and ratio of the relaxation times.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  2. Bell, J.S.: Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press, Cambridge (1987)

    MATH  Google Scholar 

  3. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  4. Bennett, C.H., Brassard, G., Crepeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  5. Bennett, C.H., Wiesner, S.J.: Communication via one- and two-particle operators on Einstein–Podolsky–Rosen states. Phys. Rev. Lett. 69, 2881–2884 (1992)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  6. Ekert, A.K.: Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. Modi, K., Brodutch, A., Cable, H., Paterek, T., Vedral, V.: The classical-quantum boundary for correlations: discord and related measures. Rev. Mod. Phys. 84, 1655–1707 (2012)

    Article  ADS  Google Scholar 

  8. Henderson, L., Vedral, V.: Classical, quantum and total correlations. J. Phys. A 34, 6899–6905 (2001)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  9. Ollivier, H., Zurek, W.H.: Quantum discord: a measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2002)

    Article  ADS  MATH  Google Scholar 

  10. Datta, A., Shaji, A., Caves, C.M.: Quantum discord and the power of one qubit. Phys. Rev. Lett. 100, 050502 (2008)

    Article  ADS  Google Scholar 

  11. Lanyon, B.P., Barbieri, M., Almeida, M.P., White, A.G.: Experimental quantum computing without entanglement. Phys. Rev. 101, 20051 (2008)

    Google Scholar 

  12. Cavalcanti, D., Aolita, L., Boixo, S., Modi, K., Piani, M., Winter, A.: Operational interpretations of quantum discord. Phys. Rev. A 83, 032324 (2011)

    Article  ADS  MATH  Google Scholar 

  13. Ali, M., Rau, A.R., Alber, G.: Quantum discord for two-qubit X states. Phys. Rev. A 81, 042105 (2010)

    Article  ADS  Google Scholar 

  14. Fanchini, F.F., Werlang, T., Brasil, C.A., Arruda, L.G.E., Caldeira, A.O.: Non-Markovian dynamics of quantum discord. Phys. Rev. A 81, 052107 (2010)

    Article  ADS  Google Scholar 

  15. Chen, Q., Zhang, C., Yu, S., Yi, X.X., Oh, C.H.: Quantum discord of two-qubit X states. Phys. Rev. 84, 042313 (2011)

    Article  ADS  Google Scholar 

  16. Maldonade-Trapp, A., Hu, A., Roa, L.: Analytical solutions and criteria for the quantum discord of two-qubit X-states. Quantum Inf. Process. 14, 1947–1958 (2015)

    Article  ADS  MATH  Google Scholar 

  17. Yurischev, M.A.: On quantum discord of general X states. Quantum Inf. Process. 14, 3399–3421 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. Luo, S.: Quantum discord for two-qubit systems. Phys. Rev. A 77, 042303 (2008)

    Article  ADS  Google Scholar 

  19. Huang, Y.: Quantum discord for two-qubit X states: analytical formula with very small worst-case error. Phys. Rev. 88, 014302 (2013)

    Article  Google Scholar 

  20. Girolami, D., Adesso, G.: Quantum discord for general two-qubit states: analytical progress. Phys. Rev. 83, 052108 (2011)

    Article  ADS  Google Scholar 

  21. Lu, X., Ma, J., Xi, Z., Wang, X.: Optimal measurements to access classical correlations of two-qubit states. Phys. Rev. 83, 012327 (2011)

    Article  Google Scholar 

  22. Breuer, H.P., Petruccione, F.: The Theory of Open Quantum Systems. Oxford University Press, Oxford (2006)

    MATH  Google Scholar 

  23. Alicki, R., Lendi, K.: Quantum Dynamical Semigroups and Applications. Springer, Berlin (2007)

    MATH  Google Scholar 

  24. Rivas, A., Huelga, S.F.: Open Quantum Systems. Springer, Berlin (2012)

    Book  MATH  Google Scholar 

  25. Yu, T., Eberly, J.H.: Finite-time disentanglement via spontaneous emission. Phys. Rev. Lett. 93, 140404 (2004)

    Article  ADS  Google Scholar 

  26. Yu, T., Hberly, J.H.: Quantum open system theory: bipartite aspects. Phys. Rev. Lett. 97, 140403 (2006)

    Article  ADS  Google Scholar 

  27. Almeida, M.P., de Melo, F., Hor-Meyll, M., Salles, A., Walborn, S.P., Rebeiro, P.H.S., Davidovich, L.: Environment-induced sudden death of entanglement. Science 316, 579–582 (2007)

    Article  ADS  Google Scholar 

  28. Laurat, J., Choi, K.S., Deng, H., Chou, C.W., Kimble, H.J.: Heralded entanglement between atomic ensembles: preparation, decoherence, and scaling. Phys. Rev. Lett. 99, 180504 (2007)

    Article  ADS  Google Scholar 

  29. Mundarain, D., Orszag, M.: Decoherence-free subspace and entanglement by interaction with a common squeezed bath. Phys. Rev. A 75, 040303 (2007)

    Article  ADS  Google Scholar 

  30. Ikram, M., Li, F., Zubairy, M.S.: Disentanglement in a two-qubit system subjected to dissipation environments. Phys. Rev. A 75, 062336 (2007)

    Article  ADS  Google Scholar 

  31. Hernandez, M., Orszag, M.: Decoherence and disentanglement for two qubits in a common squeezed reservoir. Phys. Rev. A 78, 042114 (2008)

    Article  ADS  Google Scholar 

  32. Werlang, T., Souza, S., Fanchini, F.F., Villas Boas, C.J.: Robustness of quantum discord to sudden death. Phys. Rev. A 80, 024103 (2009)

    Article  ADS  Google Scholar 

  33. Maziero, J., Celeri, L.C., Serra, R.M., Vedral, V.: Classical and quantum correlations under decoherence. Phys. Rev. A 80, 044102 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  34. Mazzola, L., Piilo, J., Maniscalco, S.: Sudden transition between classical and quantum decoherence. Phys. Rev. Lett. 104, 200401 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  35. Chanda, T., Pal, A.K., Biswas, A., Sen, A., Sen, U.: Freezing of quantum correlations under local decoherence. Phys. Rev. A 91, 062119 (2015)

    Article  ADS  Google Scholar 

  36. Maziero, J., Werlang, T., Fanchini, F.F., Celeri, L.C., Serra, R.M.: System-reservoir dynamics of quantum and classical correlations. Phys. Rev. A 81, 022116 (2010)

    Article  ADS  Google Scholar 

  37. Hua, M., Tian, D.: Preservation of the geometric quantum discord in noisy environments. Ann. Phys. 343, 132–140 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  38. Haikka, P., Johnson, T.H., Maniscalco, S.: Non-Markovianity of local dephasing channels and time-invariant discord. Phys. Rev. A 87, 010103 (2013)

    Article  ADS  Google Scholar 

  39. Ma, W., Xu, S., Shi, J., Ye, L.: Quantum correlation versus Bell-inequality violation under the amplitude damping channel. Phys. Lett. A 379, 2802–2807 (2015)

    Article  ADS  MATH  Google Scholar 

  40. Ciccarello, F., Giovannetti, V.: Creating quantum correlations through local nonunitary memoryless channels. Phys. Rev. A 85, 010102 (2012)

    Article  ADS  Google Scholar 

  41. Shi, J.D., Wang, D., Ma, W.C., Ye, L.: Enhancing quantum correlation in open-system dynamics by reliable quantum operations. Quantum Inf. Process. 14, 3569–3579 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  42. Karmakar, S., Sen, A., Bhar, A., Sarkar, D.: Effect of local filtering on freezing phenomena of quantum correlation. Quantum Inf. Process. 14, 2517–2533 (2015)

    Article  ADS  MATH  Google Scholar 

  43. Obada, A.S.F., Hessian, H.A., Mohamed, A.B.A., Hashem, M.: Stationary discord and non-local correlations via qubit damping. J. Mod. Opt. 62, 918–926 (2015)

    Article  ADS  Google Scholar 

  44. Li, Y., Xiao, X.: Recovering quantum correlations from amplitude damping decoherence by weak measurement reversal. Quantum Inf. Process. 12, 3067–3077 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  45. Wang, C., Li, C., Nie, L., Li, X., Li, J.: Classical correlation, quantum discord and entanglement for two-qubit system subject to heat bath. Opt. Commun. 284, 2393–2401 (2011)

    Article  ADS  Google Scholar 

  46. Dajka, J., Mierzejewski, M., Luczka, J., Blattmann, R., Hänggi, L.: Negativity and quantum discord in Davies environment. J. Phys. A 45, 485306 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  47. Ban, M., Kitajima, S., Shibata, F.: Decoherence of entanglement in Bloch channel. J. Phys. A 38, 4235–4245 (2005)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  48. Ban, M.: Disentanglement of two-qubit system in the Bloch channel. Opt. Commun. 283, 3812–3817 (2010)

    Article  ADS  Google Scholar 

  49. Ban, M.: Decay of two-qubit correlations in the squeezed Bloch channel. J. Mod. Opt. 59, 823–829 (2012)

    Article  ADS  Google Scholar 

  50. Huang, Y.: Computing quantum discord as NP-complete. New J. Phys. 16, 033027 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  51. Yu, T., Eberly, J.H.: Evolution from entanglement to decoherence of bipartite X states. Quantum Inf. Comp. 7, 459–468 (2007)

    MathSciNet  MATH  Google Scholar 

  52. Dajka, J., Luczka, J.: Swapping of correlation via teleportation with decoherence. Phys. Rev. A 87, 022301 (2013)

    Article  ADS  Google Scholar 

  53. Kloda, D., Dajka, J.: Temperature-independent teleportation of qubits in Davies environments. Quantum Inf. Process. 14, 135–145 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Graduate School of Humanities and Sciences, Ochanomizu University, 2-1-1 Otsuka, Bunkyo-ku, Tokyo, 112-8610, Japan

    Ikumi Kondo & Masashi Ban

Authors
  1. Ikumi Kondo
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Masashi Ban
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Masashi Ban.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kondo, I., Ban, M. Quantum discord for two-qubit systems in the Bloch channel: effects of longitudinal and transversal relaxation times. Quantum Inf Process 16, 196 (2017). https://doi.org/10.1007/s11128-017-1651-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-017-1651-6

Keywords