Skip to main content

Advertisement

Springer Nature Link
Log in

Exploring entropic uncertainty relation in the Heisenberg XX model with inhomogeneous magnetic field

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

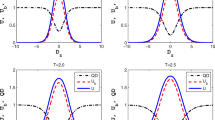
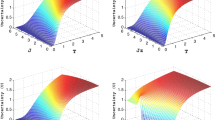
In this work, we investigate the quantum-memory-assisted entropic uncertainty relation in a two-qubit Heisenberg XX model with inhomogeneous magnetic field. It has been found that larger coupling strength J between the two spin-chain qubits can effectively reduce the entropic uncertainty. Besides, we observe the mechanics of how the inhomogeneous field influences the uncertainty, and find out that when the inhomogeneous field parameter \(b<1\), the uncertainty will decrease with the decrease of the inhomogeneous field parameter b, conversely, the uncertainty will increase with decreasing b under the condition that \(b>1\). Intriguingly, the entropic uncertainty can shrink to zero when the coupling coefficients are relatively large, while the entropic uncertainty only reduces to 1 with the increase of the homogeneous magnetic field. Additionally, we observe the purity of the state and Bell non-locality and obtain that the entropic uncertainty is anticorrelated with both the purity and Bell non-locality of the evolution state.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Heisenberg, W.: The actual content of quantum theoretical kinematics and mechanics. Z. Phys. 43, 172 (1927)

    Article  ADS  MATH  Google Scholar 

  2. Holger, F.H., Shigeki, T.: Violation of local uncertainty relations as a signature of entanglement. Phys. Rev. A 68, 032103 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  3. Bialynicki-Birula, I.: Rényi entropy and the uncertainty relations. AIP Conf. Proc. 889, 52 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. Kennard, E.H.: Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 44, 326 (1927)

    Article  ADS  MATH  Google Scholar 

  5. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  6. Robertson, H.P.: The uncertainty principle. Phys. Rev. 34, 163 (1929)

    Article  ADS  Google Scholar 

  7. Deutsch, D.: Uncertainty in quantum measurements. Phys. Rev. Lett. 50, 631–633 (1983)

    Article  ADS  MathSciNet  Google Scholar 

  8. Renes, J.M., Boileau, J.C.: Physical underpinnings of privacy. Phys. Rev. A 78, 032335 (2008)

    Article  ADS  Google Scholar 

  9. Wild, M.M., Renes, J.M.: In: Proceeding of International Symposium on Information Theory IEEE, pp. 334–338. Cambridge, Masschusetts (2012)

  10. Kraus, K.: Complementary observables and uncertainty relations. Phys. Rev. D 35, 3070 (1987)

    Article  ADS  MathSciNet  Google Scholar 

  11. Maassen, H., Uffink, J.B.M.: Generalized entropic uncertainty relations. Phys. Rev. Lett. 60, 1103 (1988)

    Article  ADS  MathSciNet  Google Scholar 

  12. Berta, M., Christandl, M., Colbeck, R., Renes, J.M., Renner, R.: The uncertainty principle in the presence of quantum memory. Nat. Phys. 6, 659–662 (2010)

    Article  Google Scholar 

  13. Kim, Y.H., Shih, Y.: Experimental realization of popper’s experiment: Violation of the uncertainty principle? Found. Phys. 29, 1849 (1999)

    Article  Google Scholar 

  14. Tomamichel, M., Renner, R.: Uncertainty relation for smooth entropies. Phys. Rev. Lett. 106, 110506 (2011)

    Article  ADS  Google Scholar 

  15. Hu, M.L., Fan, H.: Competition between quantum correlations in the quantum-memory-assisted entropic uncertainty relation. Phys. Rev. A 87, 022314 (2013)

    Article  ADS  Google Scholar 

  16. Coles, P.J., Colbeck, R., Yu, L., Zwolak, M.: Uncertainty relations from simple entropic properties. Phys. Rev. Lett. 108, 210504 (2012)

    Article  Google Scholar 

  17. Wang, D., Ming, F., Huang, A.J., Sun, W.Y., Shi, J.D., Ye, L.: Exploration of quantum-memory-assisted entropic uncertainty relations in a noninertial frame. Laser Phys. Lett. 14, 055205 (2017)

    Article  ADS  Google Scholar 

  18. Huang, A.J., Shi, J.D., Wang, D., Ye, L.: Steering quantum-memory-assisted entropic uncertainty under unital and nonunital noises via filtering operations. Quantum Inf. Process. 16, 46 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  19. Mario, B., Matthias, C., Roger, C., Renato, R.: The uncertainty principle in the presence of quantum memory. Nat. Phys. 6, 659–662 (2010)

    Article  Google Scholar 

  20. Pati, A.K., Wilde, M.M., Devi, A.R.U., Rajagopal, A.K.: Quantum discord and classical correlation can tighten the uncertainty principle in the presence memory. Phys. Rev. A 86, 042105 (2012)

    Article  ADS  Google Scholar 

  21. Hu, M.L., Fan, H.: Upper bound and shareability of quantum discord based on entropic uncertainty relations. Phys. Rev. A 88, 014105 (2013)

    Article  ADS  Google Scholar 

  22. Henderson, L., Vedral, V.: Classical, quantum and total correlations. J. Phys. A 34, 6899 (2001)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  23. Liu, S., Mu, L.Z., Fan, H.: Entropic uncertainty relations for multiple measurements. Phys. Rev. A. 91, 042133 (2015)

    Article  ADS  Google Scholar 

  24. Xiao, Y.L., et al.: Strong entropic uncertainty relations for multiple measurements. Phys. Rev. A 93, 042125 (2016)

    Article  ADS  Google Scholar 

  25. Asoudeh, M., Karimipour, V.: Thermal entanglement of spins in an inhomogeneous magnetic field. Phys. Rev. A 71, 022308 (2005)

    Article  ADS  Google Scholar 

  26. Zhang, G.F., Li, S.S.: Thermal entanglement in a two-qubit Heisenberg XXZ spin chain under an inhomogeneous magnetic field. Phys. Rev. A 72, 034302 (2005)

    Article  ADS  Google Scholar 

  27. Liang, Q.: Quantum correlations in a two-qubit Heisenberg XX model under intrinsic decoherence. Commun. Theor. Phys. 60, 391 (2013)

    Article  Google Scholar 

  28. Jonckheere, E., Langbein, F.C., Schirmer, S.G.: Information transfer fidelity in spin networks and ring-based quantum routers. Quantum Inf. Process. 14, 4751 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  29. Schirmer, S.G., Langbein. F.C.: Characterization and control of quantum spin chains and rings. In: 2014 6th International Symposium on Communications, Control and Signal Processing (ISCCSP), pp. 615–619. (2014)

  30. Hammerer, K., Vidal, G., Cirac, J.I.: Characterization of nonlocal gates. Phys. Rev. A. 66, 062321 (2002)

    Article  ADS  Google Scholar 

  31. Fardin, K., Seyed, J.A., Hamidreza, M.: Effect of spin-orbit interaction on entanglement of two-qubit Heisenberg XYZ systems in an inhomogeneous magnetic field. Phys. Rev. A 77, 042309 (2008)

    Article  Google Scholar 

  32. Man’ko, V.I., Marmo, G., Porzio, A., Solimeno, S., Ventriglia, F.: Homodyne estimation of quantum state purity by exploiting the covariant uncertainty relation. Phys Scripta 83, 4 (2011)

    MATH  Google Scholar 

  33. Xu, Z.Y., Yang, W.L., Feng, M.: Quantum-memory-assisted entropic uncertainty relation under noise. Phys. Rev. A 86, 012113 (2012)

    Article  ADS  Google Scholar 

  34. Ghosh, S., Kar, G., Sen, A., Sen, U.: Mixedness in the Bell violation versus entanglement of formation. Phys. Rev. A 64, 044301 (2001)

    Article  ADS  Google Scholar 

  35. Yao, Y., Li, H.W., Yin, Z.Q., Chen, W., Han, Z.F.: Bell violation versus geometric measure of quantum discord and their dynamical behavior. Eur. Phys. J. D 66, 295 (2012)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Science Foundation of China under Grant Nos. 11575001 and 61601002 and Anhui Provincial Natural Science Foundation under Grant No. 1508085QF139.

Author information

Authors and Affiliations

  1. School of Physics and Material Science, Anhui University, Hefei, 230601, China

    Ai-Jun Huang, Dong Wang, Jia-Ming Wang, Jia-Dong Shi, Wen-Yang Sun & Liu Ye

  2. CAS Key Laboratory of Quantum Information, University of Science and Technology of China, Hefei, 230026, China

    Dong Wang

Authors
  1. Ai-Jun Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Dong Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jia-Ming Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jia-Dong Shi
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Wen-Yang Sun
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Liu Ye
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Dong Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, AJ., Wang, D., Wang, JM. et al. Exploring entropic uncertainty relation in the Heisenberg XX model with inhomogeneous magnetic field. Quantum Inf Process 16, 204 (2017). https://doi.org/10.1007/s11128-017-1657-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-017-1657-0

Keywords