Skip to main content

Advertisement

Springer Nature Link
Log in

Exploring the tripartite entanglement and quantum phase transition in the \(XXZ+h\) model

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

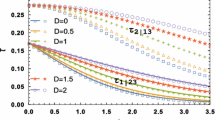
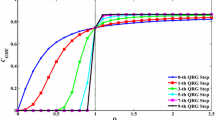
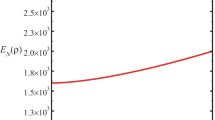
The behavior of bipartite and tripartite entanglement in Heisenberg \(XXZ+h\) spins chain is investigated with the size of system using the approach of quantum renormalization group method. In thermodynamics limit, both types of entanglement exhibit quantum phase transition (QPT). The boundary of QPT links the phases of saturated entanglement and zero entanglement. The first derivative of both entanglements becomes discontinuous at the critical point, which corresponds to the second-order phase transition. Furthermore, the amount of saturated bipartite entanglement strongly depends on relative positions of spins, while tripartite entanglement is robust than bipartite entanglement. It turns out that the tripartite entanglement can be a better candidate than bipartite entanglement for analyzing QPT and implementing quantum information tasks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, k: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  2. Einstein, A., Podolsky, P., Rosen, N.: Can quantum mechanical description of physical reality be considered complete. Phys. Rev. 47, 777 (1935)

    Article  ADS  MATH  Google Scholar 

  3. Bennett, C.H., DiVincenzo, D.P., Smolin, J.A., Wootters, W.K.: Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824 (1996)

    Article  ADS  MathSciNet  Google Scholar 

  4. Horodecki, M.: Entanglement measures. Quantum Inf. Comput. I, 3 (2001)

    MathSciNet  MATH  Google Scholar 

  5. Wootters, W.K.: Entanglement of formation and concurrence. Quantum Inf. Comput. 1, 27 (2001)

    MathSciNet  MATH  Google Scholar 

  6. Wang, X.: Threshold temperature for pairwise and many-particle thermal entanglement in the isotropic Heisenberg model. Phys. Rev. A 66, 044305 (2002)

    Article  ADS  Google Scholar 

  7. Sachdev, S.: Quantum Phase Transitions. Cambridge University Press, Cambridge (1999)

    MATH  Google Scholar 

  8. Liu, C., Xu, S., He, J., Ye, L.: Unveiling Pi-tangle and quantum phase transition in the one-dimensional anisotropic XY model. Quantum Inf. Process. 14, 2013–2024 (2015)

    Article  ADS  MATH  Google Scholar 

  9. Osterloh, A., Amico, L., Falci, G., Fazio, R.: Scaling of entanglement close to a quantum phase transition. Nature 416, 608 (2002)

    Article  ADS  Google Scholar 

  10. Vidal, G., Latorre, J., Rico, E., Kitaev, A.: Entanglement in quantum critical phenomena. Phys. Rev. Lett. 90, 227902 (2003)

    Article  ADS  Google Scholar 

  11. Vidal, G., Palacios, G., Mosseri, R.: Entanglement in a second-order quantum phase transition. Phy. Rev. A 69, 022107 (2004)

    Article  ADS  Google Scholar 

  12. Lambert, N., Emary, C., Brandes, T.: Entanglement and the phase transition in single mode superradiance. Phys. Rev. Lett. 92, 073602 (2004)

    Article  ADS  Google Scholar 

  13. Justino, L., Oliveira, D.: Bell inequalities and entanglement at quantum phase transitions in the XXZ model. Phys. Rev. A 85, 052128 (2012)

    Article  ADS  Google Scholar 

  14. Girolami, D., Adesso, G.: Observable measure of bipartite quantum correlations. Phys. Rev. Lett 108, 150403 (2012)

    Article  ADS  Google Scholar 

  15. Liu, B., Shao, B., Li, J., Zou, J., Wu, L.: Quantum and classical correlations in the one-dimensional XY model with Dzyaloshinskii–Moriya interaction. Phys. Rev. A 83, 052112 (2011)

    Article  ADS  Google Scholar 

  16. Mandel, O., Greiner, M., Widera, A., Rom, T., Hansch, W., Bloch, I.: Controlled collisions for multi-particle entanglement of optically trapped atoms. Nature 425, 937 (2003)

    Article  ADS  Google Scholar 

  17. Roos, C.F., et al.: Control and measurement of three-qubit entangled states. Science 304, 1478 (2004)

    Article  ADS  Google Scholar 

  18. de Oliveira, T.R., Rigolin, G., de Oliveira, M.C., Miranda, E.: Multipartite entanglement signature of quantum phase transitions. Phys. Rev. Lett. 97, 170401 (2006)

    Article  Google Scholar 

  19. de Oliveira, T.R., Rigolin, G., de Oliveira, M.C., Miranda, E.: Genuine multipartite entanglement in quantum phase transitions. Phys. Rev. A 73, 010305(R) (2008)

    Article  Google Scholar 

  20. Amico, L., Fazio, R., Osterloh, A., Vedral, V.: Entanglement in many-body systems Rev. Mod. Phys. 80, 517 (2008)

    Article  ADS  MATH  Google Scholar 

  21. Werlang, T., Trippe, C., Ribeiro, G.A.P., Rigolin, G.: Quantum correlations in spin chains at finite temperatures and quantum phase transitions. Phys. Rev. Lett. 105, 095702 (2010)

    Article  ADS  Google Scholar 

  22. Jafari, R.: Quantum renormalization group approach to geometric phases in spin chains. Phys. Lett. A 377, 3279 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  23. Werlang, T., Ribeiro, G.A.P., Rigolin, G.: Spotlighting quantum critical points via quantum correlations at finite temperatures. Phys. Rev. A 83, 062334 (2011)

    Article  ADS  Google Scholar 

  24. White, S.R.: Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863 (1992)

    Article  ADS  Google Scholar 

  25. White, S.R., Scalapino, D.J.: Density matrix renormalization group study of the striped Phase in the 2D tJ model. Phys. Rev. Lett. 80, 1272 (1998)

    Article  ADS  Google Scholar 

  26. Kargarian, M., Jafari, R., Langari, A.: Dzyaloshinskii–Moriya interaction and anisotropy effects on the entanglement of the Heisenberg model. Phys. Rev. A 79, 042319 (2009)

    Article  ADS  Google Scholar 

  27. Jafari, R., Kargarian, M., Langari, A., Siahatgar, M.: Phase diagram and entanglement of the Ising model with Dzyaloshinskii–Moriya interaction. Phys. Rev. B 78, 214414 (2008)

    Article  ADS  Google Scholar 

  28. Langari, A.: Quantum renormalization group of XYZ model in a transverse magnetic field. Phys. Rev. B 69, 100402 (2004)

    Article  ADS  Google Scholar 

  29. Usman, M., Ilyas, A., Khan, K.: Quantum renormalization group of the XY model in two dimensions. Phys. Rev. A 92, 032327 (2015)

    Article  ADS  Google Scholar 

  30. Ma, F.W., Liu, S.X., Kong, X.M.: Entanglement and quantum phase transition in the one-dimensional anisotropic XY model. Phys. Rev. A 83, 062309 (2011)

    Article  ADS  Google Scholar 

  31. Jafari, R., Langari, A.: Second order quantum renormalisation group of XXZ chain with next-nearest neighbour interactions. Phys. A 364, 213 (2006)

    Article  Google Scholar 

  32. Jafari, R., Langari, A.: Phase diagram of the one-dimensional S = 1/2 XXZ model with ferromagnetic nearest-neighbor and antiferromagnetic next-nearest-neighbor interactions. Phys. Rev. B 76, 014412 (2007)

    Article  ADS  Google Scholar 

  33. Ma, F.W., Liu, S.X., Kong, X.M.: Quantum entanglement and quantum phase transition in the XY model with staggered Dzyaloshinskii–Moriya interaction. Phys. Rev. A 84, 042302 (2011)

    Article  ADS  Google Scholar 

  34. Kargarian, M., Jafari, R., Langari, A.: Renormalization of concurrence: the application of the quantum renormalization group to quantum-information systems. Phys. Rev. A 76, 060304 (2007)

    Article  ADS  Google Scholar 

  35. Sun, W.Y., Shi, J.D., Wang, D., Ye, L.: Exploring the global entanglement and quantum phase transition in the spin 1/2XXZ model with Dzyaloshinskii–Moriya interaction. Quantum Inf. Process. 15, 245253 (2016)

    Google Scholar 

  36. Shi, J.D., Wang, D., Ye, L.: Genuine multipartite entanglement as the indicator of quantum phase transition in spin systems. Quantum Inf. Process. 15, 4629–4640 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  37. Martin, M.A., Sierra, G.: Analytic formulation of the density matrix renormalization group. Int. J. Mod. Phys. A 11, 3145 (1996)

    Article  ADS  Google Scholar 

  38. Martin, M.A., Sierra, G.: Real space renormalization group methods and quantum Groups. Phys. Rev. Lett. 76, 1146 (1996)

    Article  ADS  Google Scholar 

  39. Langari, A.: Phase diagram of the antiferromagnetic XXZ model in the presence of an external magnetic field. Phys. Rev. B 58, 14467 (1998)

    Article  ADS  Google Scholar 

  40. Li, M., Fei, S.M., Wang, Z.X.: A lower bound of concurrence for multipartite quantum states. J. Phys. A 42, 145303 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Physics, Quaid-i-Azam University, Islamabad, Pakistan

    Wajid Joyia & Khalid Khan

Authors
  1. Wajid Joyia
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Khalid Khan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Wajid Joyia.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Joyia, W., Khan, K. Exploring the tripartite entanglement and quantum phase transition in the \(XXZ+h\) model. Quantum Inf Process 16, 243 (2017). https://doi.org/10.1007/s11128-017-1693-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-017-1693-9

Keywords