Skip to main content
Springer Nature Link
Log in

An improved proposal on the practical quantum key distribution with biased basis

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

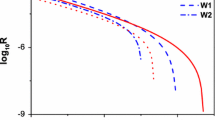
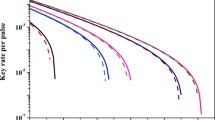
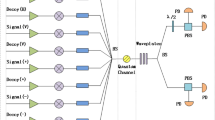
In this manuscript, we propose an improved scheme on the decoy-state quantum key distribution (QKD) under practical experimental conditions with biased basis. Compared with the standard decoy-state method with biased basis (prepare signal pulses in both X and Z basis with certain probabilities, and weak decoy pulses as well), the difference here is, we prepare signal pulses in both X and Z basis, but the weak decoy state in only X basis. In the follow-up, we adopt this scheme to conducting numerical simulations on the QKD with the mostly often used source, i.e., weak coherent source by taking statistical fluctuations into account. Furthermore, we carry out full parameter optimization on it. Numerical simulation results demonstrate that our new scheme can present a higher key generation rate and a longer transmission distance compared with standard three-intensity decoy-state method with biased basis. Moreover, it shows drastically improved performance by conducting full parameter optimization in our new scheme compared with partial optimization.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Ekert, A.: Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661 (1991)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  2. Lo, H.-K., Chau, H.F.: Unconditional security of quantum key distribution over arbitrarily long distances. Science 283, 2050 (1999)

    Article  ADS  Google Scholar 

  3. Mayers, D.: Unconditional security in quantum cryptography. J. ACM 48, 351 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bennett, C.H., Brassard, G.: Quantum cryptography: public key distribution and coin tossing. In: Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, pp. 175–179. IEEE, New York (1984)

  5. Shor, P.W., Preskill, J.: Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441 (2000)

    Article  ADS  Google Scholar 

  6. Peev, M., Pacher, C., Alleaume, R., et al.: The SECOQC quantum key distribution network in Vienna. New J. Phys. 11, 075001 (2009)

    Article  ADS  Google Scholar 

  7. Sasaki, M., Fujiwara, M., Ishizuka, H., et al.: Field test of quantum key distribution in the Tokyo QKD network. Opt. Express 19, 10387 (2011)

    Article  ADS  Google Scholar 

  8. Lo, H.-K., Chau, H.F., Ardehali, M.: Efficient quantum key distribution scheme and a proof of its unconditional security. J. Cryptol. 18, 133 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  9. Brassard, G., Ltkenhaus, N., Mor, T., Sanders, B.C.: Limitations on practical quantum cryptography. Phys. Rev. Lett. 85, 1330 (2000)

    Article  ADS  Google Scholar 

  10. Ltkenhaus, N., Jahma, M.: Quantum key distribution with realistic states: photon-number statistics in the photon-number splitting attack. New J. Phys. 4, 44.1 (2002)

    Google Scholar 

  11. Hwang, W.Y.: Quantum key distribution with high loss: toward global secure communication. Phys. Rev. Lett. 91, 057901 (2003)

    Article  ADS  Google Scholar 

  12. Wang, X.-B.: Beating the photon-number-splitting attack in practical quantum crytography. Phys. Rev. Lett. 94, 230503 (2005)

    Article  ADS  Google Scholar 

  13. Wang, Q., Wang, X.-B., Guo, G.-C.: Practical decoy-state method in quantum key distribution with a heralded single-photon source. Phys. Rev. A 75, 012312 (2007)

    Article  ADS  Google Scholar 

  14. Wang, Q., Chen, W., Xavier, G., et al.: Experimental decoy-state quantum key distribution with a sub-Poissionian heralded single-photon source. Phys. Rev. Lett. 100, 090501 (2008)

    Article  ADS  Google Scholar 

  15. Wang, Q., Wang, X.-B.: Improved practical decoy state method in quantum key distribution with parametric down-conversion source. Europhys. Lett. 79, 40001 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  16. Lo, H.-K., Ma, X.-F., Chen, K.: Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005)

    Article  ADS  Google Scholar 

  17. Ma, X.-F., Qi, B., Zhao, Y., Lo, H.-K.: Practical decoy state for quantum key distribution. Phys. Rev. A 75, 012312 (2007)

    Article  Google Scholar 

  18. Peng, C.-Z., Zhang, J., Yang, D., et al.: Experimental long-distance decoy-state quantum key distribution based on polarization encoding. Phys. Rev. Lett. 98, 010505 (2007)

    Article  ADS  Google Scholar 

  19. Wei, Z.-C., Wang, W.-L., Zhang, Z., Guo, M., Ma, X.-F.: Decoy-state quantum key distribution with biased basis choice. Sci. Rep. 3, 2454 (2013)

    Article  Google Scholar 

  20. Lucamarini, M., Patel, K., Dynes, J., et al.: Efficient decoy-state quantum key distribution with quantified security. Opt. Express 21, 24550 (2013)

    Article  ADS  Google Scholar 

  21. Lim, C.C.W., Curty, M., Walenta, N., et al.: Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. A 89, 022307 (2014)

    Article  ADS  Google Scholar 

  22. Gottesman, D., Lo, H.-K., Ltkenhaus, N., Preskill, J.: Security of quantum key distribution with imperfect devices. Quantum Inf. Comput. 4, 325 (2004)

    MathSciNet  MATH  Google Scholar 

  23. Fung, C.-H.F., Ma, X.-F., Chau, H.F.: Practical issues in quantum-key-distribution postprocessing. Phys. Rev. A 81, 012318 (2010)

    Article  ADS  Google Scholar 

  24. Zhou, Y.-H., Yu, Z.-W., Wang, X.-B.: Tightened estimation can improve the key rate of measurement-device-indepengdent quantum key distribution by more than 100%. Phys. Rev. A 89, 052325 (2014)

    Article  ADS  Google Scholar 

  25. Ma, X.-F., Fung, C.-H.F., Boileau, J.-C., Chau, H.F.: Universally composable and customizable post-processing for practical quantum key distribution. Comput. Secur. 30, 172 (2011)

    Article  Google Scholar 

  26. Wang, X.-B., Yang, L., Peng, C.-Z., Pan, J.-W.: Decoy-state quantum key distribution with both source errors and statistical fluctuations. New J. Phys. 11, 075006 (2009)

    Article  ADS  Google Scholar 

  27. Yu, Z.-W., Zhou, Y.-H., Wang, X.-B.: Statistical fluctuation analysis for measurement-device-independent quantum key distribution three-intensity decoy-state method. Phys. Rev. A 91, 032318 (2015)

    Article  ADS  Google Scholar 

  28. Xu, F.-H., Xu, H., Lo, H.-K.: Protocol choice and parameter optimization in decoy-state measurement-device-independent quantum key distribution. Phys. Rev. A 89, 052333 (2014)

    Article  ADS  Google Scholar 

  29. Wang, Q., Zhang, C.-H., Wang, X.-B.: Scheme for realizing passive quantum key distribution with heralded single-photon sources. Phys. Rew. A 93, 032312 (2016)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We gratefully acknowledge the financial support from the National Key Research and Development Program of China through Grant No. 2017YFA0304100, the National Natural Science Foundation of China through Grants Nos. 61475197, 61590932, 11774180, 61705110, the Natural Science Foundation of the Jiangsu Higher Education Institutions through Grant No. 15KJA120002, the Outstanding Youth Project of Jiangsu Province through Grant No. BK20150039, the Natural Science Foundation of Jiangsu Province through Grant No. BK20170902, and the NUPTSF through Grant No. NY217006.

Author information

Author notes

  1. Chen-Chen Mao and Jian Li have contributed equally to this work.

Authors and Affiliations

  1. Institute of Signal Processing Transmission, Nanjing University of Posts and Telecommunications, Nanjing, 210003, China

    Chen-Chen Mao, Jian Li, Jian-Rong Zhu, Chun-Mei Zhang & Qin Wang

  2. Key Lab of Broadband Wireless Communication and Sensor Network Technology, Nanjing University of Posts and Telecommunications, Ministry of Education, Nanjing, 210003, China

    Chen-Chen Mao, Jian Li, Jian-Rong Zhu, Chun-Mei Zhang & Qin Wang

  3. CAS Key Laboratory of Quantum Information, University of Science and Technology of China, Hefei, 230026, China

    Chun-Mei Zhang & Qin Wang

  4. Department of Physics, Southeast University, Nanjing, 210003, China

    Jian Li

Authors
  1. Chen-Chen Mao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jian Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jian-Rong Zhu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Chun-Mei Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Qin Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Qin Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mao, CC., Li, J., Zhu, JR. et al. An improved proposal on the practical quantum key distribution with biased basis. Quantum Inf Process 16, 256 (2017). https://doi.org/10.1007/s11128-017-1707-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-017-1707-7

Keywords