Skip to main content

Advertisement

Springer Nature Link
Log in

Qubit–qubit entanglement dynamics control via external classical pumping and Kerr nonlinearity mediated by a single detuned cavity field powered by two-photon processes

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

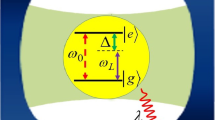
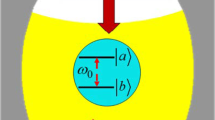
The nonlinear time-dependent two-photon Hamiltonian of a couple of classically pumped independent qubits is analytically solved, and the corresponding time evolution unitary operator, in an exact form, is derived. Using the concurrence, entanglement dynamics between the qubits under the influence of a wide range of effective parameters are examined and, in detail, analyzed. Observations analysis is documented with aid of the field phase-space distribution Wigner function. A couple of initial qubit states is considered, namely similar excited states and a Bell-like pure state. It is demonstrated that an initial Bell-like pure state is as well typical initial qubits setting for robust, regular and a high degree of entanglement. Moreover, it is established that high-constant Kerr media represent an effective tool for generating periodical entanglement at fixed time cycles of maxima reach unity forever when qubits are initially in a Bell-like pure state. Further, it is showed that the medium strength of the classical pumping stimulates efficiently qubits entanglement, specially, when the interaction occurs off resonantly. However, the high-intensity pumping thermalizes the coherent distribution of photons, thus, the least photons number is used and, hence, the least minimum degree of qubits entanglement could be created. Furthermore, when the cavity field and external pumping are detuned, the external pumping acts like an auxiliary effective frequency for the cavity, as a result, the field Gaussian distribution acquires linear chirps, and consequently, more entanglement revivals appear in the same cycle during timescale.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32
Fig. 33
Fig. 34
Fig. 35
Fig. 36

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Walls, D.F., Milburn, G.J.: Quantum Optics, 2nd edn. Springer, Berlin (2008)

    Book  MATH  Google Scholar 

  2. Brukner, C., Zukowski, M., Zeilinger, A.: Quantum communication complexity protocol with two entangled qutrits. Phys. Rev. Lett. 89, 197901 (2002)

    Article  ADS  Google Scholar 

  3. Adhikari, S., Majumdar, A.S., Roy, S., Ghosh, B., Nayak, N.: Teleportation via maximally and non-maximally entangled mixed states. Quant. Inf. Comput 10(5 & 6), 03980419 (2010)

    MATH  MathSciNet  Google Scholar 

  4. Yupapin, P.P.: Generalized quantum key distribution via micro ring resonator for mobile telephone networks. Opt. Int. J. Light Electron Opt. 121(5), 422–425 (2010)

    Article  Google Scholar 

  5. Waks, E., Zeevi, A., Yamamoto, Y.: Security of quantum key distribution with entangled photons against individual attacks. Phys. Rev. A 65, 52310 (2002)

    Article  ADS  Google Scholar 

  6. Marzolino, U., Buchleitner, A.: Quantum teleportation with identical particles. Phys. Rev. A 91, 032316 (2015)

    Article  ADS  MATH  Google Scholar 

  7. Albeverio, S., Fei, S.M., Yang, W.L.: Quantum teleportation: from pure to mixed states and standard to optimal. E-print: arXiv:quant-ph/0308009 (2003)

  8. Roy, S., Ghosh, B.: A revisit to non-maximally entangled mixed states: teleportation witness, noisy channel and discord. Quant. Inf. Process. 16(4), 1–13 (2017)

    Article  MATH  MathSciNet  Google Scholar 

  9. Benenti, G., Casati, G., Strini, G.: Principle of Quantum Computation and Information. World Scientific, Singapore (2005)

    MATH  Google Scholar 

  10. Deng, F.G., Long, G.L., Liu, X.S.: Two-step quantum direct communication protocol using the Einstein–Podolsky–Rosen pair block. Phys. Rev. A 68, 042317 (2003)

    Article  ADS  Google Scholar 

  11. Chao, D.S., Zhi, J.: Review on the study of entanglement in quantum computation speedup. Chin. Sci. Bull. 52(16), 21612166 (2007)

    Google Scholar 

  12. Jozsa, R., Linden, N.: On the role of entanglement in quantum-computational speed-up. In: Proceedings of the Royal Society of London. Series A. Mathematical, Physical and Engineering Sciences, vol. 459, pp. 2011–2032 (2003)

  13. Hacker, B., Welte, S., Rempe, G., Ritter, S.: A photonphoton quantum gate based on a single atom in an optical resonator. Nature 536, 193196 (2016)

    Article  Google Scholar 

  14. Vandersypen, L.M.K., Steffen, M., Breyta, G., Yannoni, C.S., Sherwood, M.H., Chuang, I.L.: Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 414, 883 (2001)

    Article  ADS  Google Scholar 

  15. Chen, J., Altepeter, J.B., Medic, M., Lee, K.F., Gokden, B., Hadfield, R.H., Nam, S.W., Kumar, P.: Demonstration of a quantum controlled-NOT gate in the telecommunications band. Phys. Rev. Lett. 100, 133603 (2008)

    Article  ADS  Google Scholar 

  16. O’Brien, J.L., Pryde, G.J., White, A.G., Ralph, T.C., Branning, D.: Demonstration of an all-optical quantum controlled-NOT gate. E-print: arXiv:quant-ph/0403062 (2004)

  17. Giri, P.R., Korepin, V.E.: A review on quantum search algorithms. E-print: arXiv:1602.02730 [quant-ph] (2016)

  18. Fushman, I., Englund, D., Faraon, A., Stoltz, N., Petroff, P., Vucković, J.: Controlled phase shifts with a single quantum dot. Science 320(5877), 769–772 (2008)

    Article  ADS  Google Scholar 

  19. Das, A., Ronen, Y., Heiblum, M., Mahalu, D., Kretinin, A.V., Shtrikman, H.: High-efficiency Cooper pair splitting demonstrated by two-particle conductance resonance and positive noise cross-correlation. Nat Commun (London) 3, 1165 (2012)

    Article  ADS  Google Scholar 

  20. You, J.Q., Tsai, J.S., Nori, F.: Scalable quantum computing with Josephson charge qubits. Phys. Rev. Lett. 89, 197902 (2002)

    Article  ADS  Google Scholar 

  21. You, J.Q., Tsai, J.S., Nori, F.: Controllable manipulation and entanglement of macroscopic quantum states in coupled charge qubits. Phys. Rev. B 68, 024510 (2003)

    Article  ADS  Google Scholar 

  22. Miranowicz, A., Paprzycka, M., Liu, Y-x, Bajer, J., Nori, F.: Two-photon and three-photon blockades in driven nonlinear systems. Phys. Rev. A 87, 023809 (2013)

    Article  ADS  Google Scholar 

  23. You, J.Q., Hu, X., Nori, F.: Correlation-induced suppression of decoherence in capacitively coupled Cooper-pair boxes. Phys. Rev. B 72, 144529 (2005)

    Article  ADS  Google Scholar 

  24. Georgescu, I.M., Ashhab, S., Nori, F.: Quantum simulation. Rev. Mod. Phys. 86, 153 (2014)

    Article  ADS  Google Scholar 

  25. Buluta, Iulia, Nori, Franco: Quantum simulators. Science 326, 108–111 (2009)

    Article  ADS  Google Scholar 

  26. Mabuchi, H., Doherty, A.C.: Cavity quantum electrodynamics: coherence in context. Science 298, 1372 (2002)

    Article  ADS  Google Scholar 

  27. You, J.Q., Nori, F.: Superconducting circuits and quantum information. Phys. Today 58(11), 42–47 (2005)

    Article  Google Scholar 

  28. You, J.Q., Nori, F.: Atomic physics and quantum optics using superconducting circuits. Nature 474, 589 (2011)

    Article  ADS  Google Scholar 

  29. Xiang, Z.-L., Ashhab, S., You, J.Q., Nori, F.: Hybrid quantum circuits: superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 85, 623 (2013)

    Article  ADS  Google Scholar 

  30. Wang, Y.-C., Liu, J.-M.: entanglement swapping and concentration in the two-photon Jaynes–Cummings model. Int. J. Mod. Phys. B 21, 2805 (2007)

    Article  ADS  Google Scholar 

  31. Li, P.B., Gu, Y., Gong, Q.H., Guo, G.C.: Quantum-information transfer in a coupled resonator waveguide. Phys. Rev. A 79, 042339 (2009)

    Article  ADS  Google Scholar 

  32. Zheng, S.-B., Guo, G.-C.: Efficient scheme for two-atom entanglement and quantum information processing in cavity QED. Phys. Rev. Lett. 85, 2392 (2000)

    Article  ADS  Google Scholar 

  33. Osnaghi, S., Bertet, P., Auffeves, A., Maioli, P., Brune, M., Raimond, J.M., Haroche, S.: Coherent control of an atomic collision in a cavity. Phys. Rev. Lett. 87, 037902 (2001)

    Article  ADS  Google Scholar 

  34. Hong, J., Lee, H.-W.: Quasideterministic generation of entangled atoms in a cavity. Phys. Rev. Lett. 89, 237901 (2002)

    Article  ADS  Google Scholar 

  35. Yang, M., Yi, Y.-M., Cao, Z.-L.: scheme for preparation of W state via cavity QED. Int. J. Quantum. Inf. 2, 231 (2004)

    Article  MATH  Google Scholar 

  36. Feng, X.-L., Zhang, Z.-M., Li, X.-D., Gong, S.-Q., Xu, Z.-Z.: Entangling distant atoms by interference of polarized photons. Phys. Rev. Lett. 90, 217902 (2003)

    Article  ADS  Google Scholar 

  37. Duan, L.-M., Kimble, H.J.: Efficient engineering of multiatom entanglement through single-photon detections. Phys. Rev. Lett. 90, 253601 (2003)

    Article  ADS  Google Scholar 

  38. Browne, D.E., Plenio, M.B., Huelga, S.F.: Robust creation of entanglement between ions in spatially separate cavities. Phys. Rev. Lett. 91, 067901 (2003)

    Article  ADS  Google Scholar 

  39. Yang, C.-P., Chu, S.-I., Han, S.: Quantum information transfer and entanglement with SQUID qubits in cavity QED: a dark-state scheme with tolerance for nonuniform device parameter. Phys. Rev. Lett. 92, 117902 (2004)

    Article  ADS  Google Scholar 

  40. Marr, C., Beige, A., Rempe, G.: Entangled-state preparation via dissipation-assisted adiabatic passages. Phys. Rev. A 68, 033817 (2003)

    Article  ADS  Google Scholar 

  41. Amniat-Talab, M., Guérin, S., Jauslin, H.R.: Decoherence-free creation of atom-atom entanglement in a cavity via fractional adiabatic passage. Phys. Rev. A 72, 012339 (2005)

    Article  ADS  MATH  Google Scholar 

  42. Ashhab, S., Nori, F.: Qubit-oscillator systems in the ultrastrong-coupling regime and their potential for preparing nonclassical states. Phys. Rev. A 81, 042311 (2010)

    Article  ADS  Google Scholar 

  43. Nation, P.D., Johansson, J.R., Blencowe, M.P., Nori, F.: Colloquium: stimulating uncertainty: amplifying the quantum vacuum with superconducting circuits. Rev. Mod. Phys. 84, 1–24 (2012)

  44. Liu, Yu-xi, Wei, L.F., Nori, Franco: Preparation of macroscopic quantum superposition states of a cavity field via coupling to a superconducting charge qubit. Phys. Rev. A 71, 063820 (2005)

  45. Schneider, S., Milburn, G.J.: Entanglement in the steady state of a collective-angular-momentum (Dicke) model. Phys. Rev. A 65, 042107 (2002)

    Article  ADS  Google Scholar 

  46. Kim, M.S., Lee, J., Ahn, D., Knight, P.L.: Entanglement induced by a single-mode heat environment. Phys. Rev. A 65, 040101(R) (2002)

    Article  ADS  Google Scholar 

  47. Plenio, M.B., Huelga, S.F., Beige, A., Knight, P.L.: Cavity-loss-induced generation of entangled atoms. Phys. Rev. A 59, 2468 (1999)

    Article  ADS  Google Scholar 

  48. Beige, A., Bose, S., Braun, D., Huelga, S.F., Knight, P.L., Plenio, M.B., Verdal, V.: Entangling atoms and ions in dissipative environments. J. Mod. Opt. 47, 2583 (2000)

    Article  ADS  Google Scholar 

  49. Cabrillo, C., Cirac, J.I., Garcia-Fernandez, P., Zoller, P.: Creation of entangled states of distant atoms by interference. Phys. Rev. A 59, 1025 (1999)

    Article  ADS  Google Scholar 

  50. Ficek, Z., Tanaś, R.: Entanglement induced by spontaneous emission in spatially extended two-atom systems. J. Mod. Opt. 50, 2765 (2003)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  51. Tanaś, R., Ficek, Z.: Entangling two atoms via spontaneous emission. J. Opt. B 6, s90 (2004)

    Article  ADS  Google Scholar 

  52. Tanas, R., Ficek, Z.: Entanglement of two atoms. Fortschr. Phys. 51, 230 (2003)

    Article  MATH  Google Scholar 

  53. Flores-Hidalgo, G., Rojas, M., Rojas, O.: Entanglement of a two-atom system driven by the quantum vacuum in arbitrary cavity size. Phys. Lett. A 381(18), 1548 (2017)

    Article  ADS  Google Scholar 

  54. Ma, J.-M., Jiao, Z.-Y., Li, N.: Quantum entanglement in two-photon Tavis–Cummings model with a Kerr nonlinearity. Int. J. Theor. Phys. 46, 2550 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  55. Ateto, M.S.: Control of a nonlocal entanglement in the micromaser via two quanta non-linear processes induced by dynamic stark shift. Int. J. Theor. Phys. 48, 545 (2009)

    Article  MATH  Google Scholar 

  56. Singh, S.P., Singh, N.: Nonlinear effects in optical fibers: origin, management and applications. Prog. Electromagn. Res. (PIER) 73, 249 (2007)

    Article  Google Scholar 

  57. Lü, X.-Y., Zhang, W.-M., Ashhab, S., Ying, W., Nori, F.: Quantum-criticality-induced strong Kerr nonlinearities in optomechanical systems. Sci. Rep. 3, 2943 (2013)

    Article  Google Scholar 

  58. Gong, Z.R., Ian, H., Liu, Yu-xi, Sun, C.P., Nori, Franco: Effective Hamiltonian approach to the Kerr nonlinearity in an optomechanical system. Phys. Rev. A 80, 065801 (2009)

  59. Aspelmeyer, M., Meystre, P., Schwab, K.: Quantum optomechanics. Phys. Today 65(7), 2935 (2012)

    Article  Google Scholar 

  60. Kippenberg, T.J., Vahala, K.J.: Cavity optomechanics: back-action at the mesoscale. Science 321, 11721176 (2008)

    Article  Google Scholar 

  61. Marquardt, F., Girvin, S.M.: Trend: optomechanics. Physics 2, 40 (2009)

    Article  Google Scholar 

  62. Li, C.: Nonlinear Optics: Principles and Applications. Springer. ISBN: 978-981-10-1487-1 (Print) 978-981-10-1488-8 (Online) (2017)

  63. Mourou, A.G., Tajima, T., Bulanov, V.S.: Optics in the relativistic regime. Rev. Mod. Phys. 78(2), 309 (2006)

    Article  ADS  Google Scholar 

  64. Vaziri, M.R.R.: Comment on Nonlinear refraction measurements of materials using the moiré deflectometry. Opt. Commun. 357, 200 (2015)

    Article  ADS  Google Scholar 

  65. Agrawal, G.P.: Nonlinear Fiber Optics, 3rd edn. Academic Press, San Diego (2001)

    MATH  Google Scholar 

  66. Hamedi, H.R., Juzeliūnas, G.: Phase-sensitive Kerr nonlinearity for closed-loop quantum systems. Phys. Rev. A 91, 053823 (2015)

    Article  ADS  Google Scholar 

  67. Dey, T.N., Agarwal, G.S.: Observable effects of Kerr nonlinearity on slow light. Phys. Rev. A 76, 015802 (2007)

    Article  ADS  Google Scholar 

  68. Ali, H., Ziauddin, Ahmad, T.: The effect of Kerr nonlinearity and Doppler broadening on slow light propagation. Commun. Theor. Phys. 60, 87 (2012)

    Article  Google Scholar 

  69. Würthner, F., Wortmann, R., Meerholz, K.: Chromophore design for photorefractive organic materials. Chem. Phys. Chem. 32, 17 (2002)

    Article  Google Scholar 

  70. You, C.-Y., Shin, S.-C.: Generalized analytic formulae for magneto-optical Kerr effects. J. App. Phys. 84, 541 (1998)

    Article  ADS  Google Scholar 

  71. Versteegh, M.A.M., Dijkhuis, J.I.: Ultrafast all-optical shutter based on two-photon absorption. Opt. Lett. 36(15), 2776–2778 (2011)

    Article  ADS  Google Scholar 

  72. Hu, L.-Y., Duan, Z.-L., Xu, X.-X., Wang, Z.-S.: Wigner function evolution in self-Kerr Medium derived by entangled state representation. arXiv:1010.0584 [quant-ph] 25 Sep (2010)

  73. Boumeester, D., Ekert, A., Zeilinger, A. (eds.): The Physics of Quantum Information: Quantum Cryptography, Quantum Teleportation. Quantum Computing. Springer, Berlin (2000)

    Google Scholar 

  74. Liu, Yu-xi, Wei, L.F., Nori, F.: Generation of nonclassical photon states using a superconducting qubit in a microcavity. Europhys. Lett. 67, 941–947 (2004)

    Article  ADS  Google Scholar 

  75. Y-x, Liu, Xu, X.-W., Miranowicz, A., Nori, F.: From blockade to transparency: controllable photon transmission through a circuit-QED system. Phys. Rev. A 89, 043818 (2014)

    Article  ADS  Google Scholar 

  76. Miranowicz, A., Paprzycka, M., Pathak, A., Nori, F.: Phase-space interference of states optically truncated by quantum scissors: generation of distinct superpositions of qudit coherent states by displacement of vacuum. Phys. Rev. A 89, 033812 (2014)

    Article  ADS  Google Scholar 

  77. Miranowicz, A., Bartkowiak, M., Wang, X., Liu, Y-x, Nori, F.: Testing nonclassicality in multimode fields: a unified derivation of classical inequalities. Phys. Rev. A 82, 013824 (2010)

    Article  ADS  Google Scholar 

  78. Bartkowiak, M., Miranowicz, A., Wang, X., Liu, Y-x, Leoński, W., Nori, F.: Sudden vanishing and reappearance of nonclassical effects: general occurrence of finite-time decays and periodic vanishings of nonclassicality and entanglement witnesses. Phys. Rev. A 83, 053814 (2011)

    Article  ADS  Google Scholar 

  79. Schleich, W.P.: Quantum Optics in Phase Space. Wiley-VCH, Berlin (2001)

    Book  MATH  Google Scholar 

  80. Stobińska, M., Milburn, G.J., Wódkiewicz, K.: Wigner function evolution of quantum states in the presence of self-Kerr interaction. Phys. Rev. A 78, 013810 (2008)

    Article  ADS  Google Scholar 

  81. Bertet, P., Auffeves, A., Maioli, P., Osnaghi, S., Meunier, T., Brune, M., Raimond, J.M., Haroche, S.: Direct measurement of the Wigner function of a one-photon fock state in a cavity. Phys. Rev. Lett. 89(20), 200402 (2002)

    Article  ADS  Google Scholar 

  82. Kenfack, A., Życkowski, K.: Negativity of the Wigner function as an indicator of non-classicality. J. Opt. B: Quantum Semiclassical Opt. 6, 396 (2004)

    Article  ADS  MathSciNet  Google Scholar 

  83. Ourjoumtsev, A., Dantan, A., Tualle-Brouri, R., Grangier, P.: Increasing entanglement between gaussian states by coherent photon subtraction. Phys. Rev. Lett. 98, 030502 (2007)

    Article  ADS  Google Scholar 

  84. Neergaard-Nielsen, J.S., Melholt Nielsen, B., Hettich, C., Molmer, K., Polzik, E.S.: Generation of a superposition of odd photon number states for quantum information networks. Phys. Rev. Lett. 97, 083604 (2006)

    Article  ADS  Google Scholar 

  85. Jeong, H., Lund, A.P., Ralph, T.C.: Production of superpositions of coherent states in traveling optical fields with inefficient photon detection. Phys. Rev. A 72, 013801 (2005)

    Article  ADS  Google Scholar 

  86. Veitch, V., Ferrie, C., Gross, D., Emerson, J.: Negative quasi-probability as a resource for quantum computation. New J. Phys. 14, 113011 (2012)

    Article  ADS  Google Scholar 

  87. Mari, A., Eisert, J.: Positive Wigner functions render classical simulation of quantum computation efficient. Phys. Rev. Lett. 109, 230503 (2012)

    Article  ADS  Google Scholar 

  88. Veitch, V., Wiebe, N., Ferrie, C., Emerson, J.: Efficient simulation scheme for a class of quantum optics experiments with non-negative Wigner representation. New J. Phys. 15, 013037 (2013)

    Article  ADS  Google Scholar 

  89. Hardy, Y., Steeb, W.-H., Stoop, R.: Entanglement, disentanglement and Wigner functions. Phys. Scr. 69, 166 (2004)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  90. Dahl, J.P., Mack, H., Wolf, A., Schleich, W.P.: Entanglement versus negative domains of Wigner functions. Phys. Rev. A 74, 042323 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  91. Li-Yun, H., Hong-Yi, F.: Entanglement involved in pair coherent state studied via Wigner function formalism. Commun. Theor. Phys. (Beijing, China) 52, 1071 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  92. Mišta Jr., L., Filip, R., Furusawa, A.: Continuous-variable teleportation of a negative Wigner function. Phys. Rev. A 82, 012322 (2010)

    Article  ADS  Google Scholar 

  93. Santos, M.F., Lutterbach, L.G., Davidovich, L.: Probing entanglement in phase space: signature of GHZ states in the Wigner function. J. Opt. B Quantum Semiclassical Opt. 3, S55 (2001)

    Article  Google Scholar 

  94. Fan, H.-Y., Jiang, N.-Q.: Tripartite entangled Wigner operator, the Wigner function and its marginal distributions. J. Opt. B Quantum Semiclassical Opt. 5, 283 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  95. Ateto, M.S.: Atom-atom entanglement dynamics enhancement via classically driven atoms coupled to a non-resonance single mode cavity field filled with nonlinear Kerr media. Int. J. Quant. Inf. 13(5), 1550034 (2015)

    Article  MATH  Google Scholar 

  96. Solano, E., Agarwal, G.S., Walther, H.: Strong-driving-assisted multipartite entanglement in cavity QED. Phys. Rev. Lett. 90, 027903 (2003)

    Article  ADS  Google Scholar 

  97. Akhtarshenas, S.J., Khezrian, M.: Entanglement dynamics and decoherence of an atom coupled to a dissipative cavity field. Eur. Phys. J. D 57, 271 (2010)

    Article  ADS  Google Scholar 

  98. Burlak, G., Starostenko, O., Hernandez, J.A.: The dynamics of coupled atom and field assisted by continuous external pumping. Rev. Mex. Fis. 52(3), 213 (2006)

    Google Scholar 

  99. Zheng, S.-B.: Jaynes–Cummings model with a collective atomic mode. Phys. Rev. A 77, 045802 (2008)

    Article  ADS  Google Scholar 

  100. Escudero-Jiménez, J.L., Juárez-Amaro, R., Mar-Sarao, R., Moya-Cessa, H.: Effective Hamiltonian for a two-level atom interacting with two fields. I. R. E. Phys. 2, 281 (2008)

    Google Scholar 

  101. Klimov, A.B., Sainz, I., Saavedra, C.: Effective resonant interactions via a driving field. J. Opt. B Quantum Semiclassical Opt. 6, 448 (2004)

    Article  ADS  Google Scholar 

  102. Moya-Cessa, H.: Decoherence in atomfield interactions: a treatment using superoperator techniques. Phys. Rep. 432, 1 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  103. Ateto, M.S.: Optimizing of maximally-entangled state by means of nonlinearity. Int. J. Quant. Inf. 5(4), 535 (2007)

    Article  MATH  Google Scholar 

  104. Ateto, M.S.: An investigation of a nonlocal entanglement of two uncoupled atoms embedded in a coherent cavity field and the associated phase space distribution: one quantum nonlinear process. Int. J. Quant. Inf. 8(6), 1045 (2010)

    Article  MATH  Google Scholar 

  105. Alsing, P., Zubairy, M.S.: Collapse and revivals in a two-photon absorption process. J. Opt. Soc. Am. B 4, 177 (1987)

    Article  ADS  Google Scholar 

  106. Puri, R.R., Bullough, R.K.: Quantum electrodynamics of an atom making two-photon transitions in an ideal cavity. J. Opt. Soc. Am. B 5, 2021 (1988)

    Article  ADS  Google Scholar 

  107. Joshi, A., Puri, R.R.: Quantum electrodynamics of a rydberg atom making two-photon transitions in the binomial state of the field in a lossless cavity. J. Mod. Opt. 36, 215 (1989)

    Article  ADS  Google Scholar 

  108. Gantsog, Ts, Joshi, A., Tanaś, R.: Phase properties of one- and two-photon Jaynes–Cummings models with a Kerr medium. Quantum Semiclassical Opt. 8, 445 (1996)

    Article  ADS  Google Scholar 

  109. Demkowicz-Dobrzański, R., Jarzyna, M., Kolodyński, J.: Quantum limits in optical interferometry. arXiv:1405.7703v2 [quant-ph] 8 Oct (2014)

  110. Wootters, W.K.: Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245 (1998)

    Article  ADS  MATH  Google Scholar 

  111. Hudson, R.L.: When is the Wigner quasi-probability density non-negative? Rep. Math. Phys. 6, 249 (1974)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  112. Verma, A., Manchanda, P., Varshney, A.D., Chauhan, P.K.: Phase space distribution functions for qudit states using QUTIP. Int. J. Res. Eng. Tech. Manag. 3(3), 1 (2015). ID: IJRETM-2015-03-03-009

    Google Scholar 

  113. de León-Montiel, R.J., Moya-Cessa, H.M., Soto-Eguibar, F.: Nonlinear coherent states for the Susskind–Glogower operators. Rev. Mex. Fis. 57(3), 133 (2011)

    Google Scholar 

  114. de León-Montiel, R.J., Moya-Cessa, H.M.: Generation of squeezed Schrdinger cats in a tunable cavity filled with a Kerr medium. J. Opt. 17(6), 065202 (2015)

    Article  ADS  Google Scholar 

  115. Tuguldur, B., Gantsog, T.S.: Some features of the Driven Jaynes–Cummings system. arXiv:1212.3211 [quant-ph] 13 Dec (2012)

  116. Wilson-Gordon, A.D., Buzek, V., Knight, P.L.: Statistical and phase properties of displaced Kerr states. Phys. Rev. 44(11), 7647 (1991)

    Article  ADS  Google Scholar 

  117. Miranowicz, A., Bartkiewicz, K., Pathak, A., Peirina Jr., J., Chen, Y.-N., Nori, F.: Statistical mixtures of states can be more quantum than their superpositions: comparison of nonclassicality measures for single-qubit states. Phys. Rev. A 91, 042309 (2015)

    Article  ADS  Google Scholar 

  118. Boyd, R.W.: Nonlinear Optics. Academic, San Diego (1992)

    Google Scholar 

  119. Paris, M.G.A.: Generation of mesoscopic quantum superpositions through Kerr-stimulated degenerate downconversion. J. Opt. B Quantum Semiclassical Opt. 1, 662 (1999)

    Article  ADS  Google Scholar 

  120. Anderson, D., Desaix, M., Lisak, M., Quiroga-Teixeiro, M.L.: Wave breaking in nonlinear-optical fibers. J. Opt. Soc. Am. B. 9(8), 1358 (1992)

    Article  ADS  Google Scholar 

  121. Gevorgyan, T.V., Shahinyan, A.R., Kryuchkyan, G.Y.: Quantum interference and sub-Poissonian statistics for time-modulated driven dissipative nonlinear oscillators. Phys. Rev. A 79, 053828 (2009)

    Article  ADS  Google Scholar 

  122. Stobińska, M., Villar, A.S., Leuchs, G.: Generation of Kerr non-Gaussian motional states of trapped ions. EPL 94, 54002 (2011). doi:10.1209/0295-5075/94/54002

    Article  ADS  Google Scholar 

  123. Yukawa, M., Miyata, K., Mizuta, T., Yonezawa, H., Marek, P., Filip, R., Furusawa, A.: Generating superposition of up-to three photons for continuous variable quantum information processing. Opt. Express 21, 5529 (2013)

    Article  ADS  Google Scholar 

  124. L’Huillier, A., Piraux, B., Rzazewski, K.: Super-Intense Laser-Atom Physics. Springer. ISBN 978-1-4615-7963-2

  125. Zuppardo, M., Santos, J.P., De Chiara, G., Paternostro, M., Semião, F.L., Palma, G.M.: Cavity-aided quantum parameter estimation in a bosonic double-well Josephson junction. Phys. Rev. A 91, 033631 (2015)

    Article  ADS  Google Scholar 

  126. Eggleton, B.J., Lenz, G., Slusher, R.E., Litchinitser, N.M.: Compression of optical pulses spectrally broadened by self-phase modulation with a fiber Bragg grating in transmission. App. Opt. 37(30), 7055 (1998)

    Article  ADS  Google Scholar 

  127. Liu, B., Yamilov, A., Caoa, H.: Effect of Kerr nonlinearity on defect lasing modes in weakly disordered photonic crystals. Appl. Phys. Lett. 83(6), 1092 (2003)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The author would like to express his great thanks to the reviewer for precious comments and remarks which have contributed effectively in improving the manuscript in many ways. Also, the author is grateful to the Editor for helpful advice.

Author information

Authors and Affiliations

  1. Mathematics Department, Faculty of Science at Qena, South Valley University, Qena, 83523, Egypt

    M. S. Ateto

  2. Mathematics Department, Faculty of Science, Gazan University, Gazan, Kingdom of Saudi Arabia

    M. S. Ateto

Authors
  1. M. S. Ateto
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to M. S. Ateto.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ateto, M.S. Qubit–qubit entanglement dynamics control via external classical pumping and Kerr nonlinearity mediated by a single detuned cavity field powered by two-photon processes. Quantum Inf Process 16, 267 (2017). https://doi.org/10.1007/s11128-017-1714-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-017-1714-8

Keywords