Renormalization of global entanglement and Bell nonlocality in the Ising model with a transverse field

Abstract

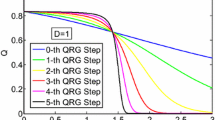
By combining quantum renormalization group approach and critical theory, we investigate the performance of global entanglement and Bell nonlocality in quantum phase transition (QPT) that occurred in Ising model with a transverse field (ITF). After several iterations, both of them gradually develop two different saturated values relevant to the Ising phase and paramagnetic phase. Moreover, we proved that the inherent block–block correlation is strong enough to violate the quantum nonlocality. What is more, we derive an exact relation between global entanglement and Bell nonlocality for the given case. To serve further insight, the nonanalytic and scaling behaviors are analyzed.

Appendix

In this appendix, we will first detail how the ITF model is renormalized by exploiting the QRG method. The Hamiltonian of the ITF model in the z direction on a periodic chain of N site is

$$\begin{aligned} H=-J\sum _{i=1}^N {\left[ {\sigma _i^x \sigma _{i+1}^x +g\sigma _i^z } \right] }, \end{aligned}$$

(A1)

By implementing the Kadanoff’s block method, Hamiltonian (A1) can be rewritten as

$$\begin{aligned} H=H^\mathrm{B}+H^\mathrm{BB}, \end{aligned}$$

(A2)

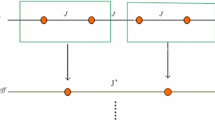
where $H^\mathrm{B}$ is the block Hamiltonian and $H^\mathrm{BB}$ is the interblock Hamiltonian. Here, we choose two sites as a block and the decomposition is shown in Fig. 5.

Fig. 5

(Color online) The decomposition of ITF model by implementing the Kadanoff’s block approach. The Hamiltonian of the system is divided into two parts, i.e., block Hamiltonian $H^\mathrm{B}$ and interblock Hamiltonian $H^\mathrm{BB}$

Simultaneously, the specific forms of Hamiltonian $H^\mathrm{B}$ and $H^\mathrm{BB}$ are

$$\begin{aligned} H^\mathrm{B}= & {} \sum _L^{N/2} {h_L^A }, \end{aligned}$$

(A3)

$$\begin{aligned} H^\mathrm{BB}= & {} -J\sum _L^{N/2} {\left[ {\sigma _{L,2}^x \sigma _{L+1,1}^x +g\sigma _L^z } \right] }, \end{aligned}$$

(A4)

with $h_L^A =-J\left[ {\sigma _{L,1}^x \sigma _{L,2}^x +g\sigma L^z } \right]$ is the Lth block Hamiltonian. A remark is in order; choosing two-site block is essential here to get a self-similarity Hamiltonian after each iterative step.

In terms of the matrix product states, the Lth block Hamiltonian can be exactly diagonalized and solved. Then, we can obtain two degenerate ground states which are used to construct the projection operators. With $\left| \uparrow \right\rangle$ and $\left| \downarrow \right\rangle$ defined as the eigenstates of operator $\sigma ^{z}$, both degenerate ground states are

$$\begin{aligned} \left| {\phi _0 } \right\rangle= & {} \frac{1}{\sqrt{1+\left( {g+\sqrt{1+g^{2}}} \right) ^{2}}}\left[ {\left( {g+\sqrt{1+g^{2}}} \right) \left| {\downarrow \downarrow } \right\rangle +\left| {\uparrow \uparrow } \right\rangle } \right] , \end{aligned}$$

(A5)

$$\begin{aligned} \left| {\phi _0 ^{\prime }} \right\rangle= & {} \frac{1}{\sqrt{1+\left( {g+\sqrt{1+g^{2}}} \right) ^{2}}}\left[ {\left( {g+\sqrt{1+g^{2}}} \right) \left| {\downarrow \uparrow } \right\rangle +\left| {\uparrow \downarrow } \right\rangle } \right] . \end{aligned}$$

(A6)

To eliminate the higher energy of the system and retain the lower, the projection operator $P_0$ is composed of its lowest energy eigenstates. Then, the effective Hamiltonian $H^\mathrm{eff}$ and original Hamiltonian H have in common the low-lying spectrum, which can be given by the projection operator, i.e., $H^\mathrm{eff}=P_0^\dagger HP_0$ wherein $P_0^\dagger$ is the Hermitian operator of $P_0$. In the effective Hamiltonian, we consider only the first-order correction in the perturbation theory, which is

$$\begin{aligned} H^\mathrm{eff}=H_0^\mathrm{eff} +H_1^\mathrm{eff} =P_0^\dagger H^\mathrm{B}P_0 +P_0^\dagger H^\mathrm{BB}P_0. \end{aligned}$$

(A7)

At the same time, the projection operator $P_0$ can be put in a factorized form

$$\begin{aligned} P_0 =\prod _{i=1}^{N/2} {P_0^L }, \end{aligned}$$

(A8)

where the specific form of $P_0^L$ is

$$\begin{aligned} P_0^L =\left| \Uparrow \right\rangle _L \left\langle {\phi _0 } \right| +\left| \Downarrow \right\rangle _L \left\langle {\phi _0 } \right| \end{aligned}$$

(A9)

with $\left| \Uparrow \right\rangle _L$ and $\left| \Downarrow \right\rangle _L$ are the renamed states of the Lth block to represent the effective site degrees of freedom. Then, the effective Hamiltonian of the renormalized ITF model can be cast into with the scaled couplings.

Now, we analytically present the derivation of global entanglement for the pure state $\rho$. Explicitly, in the orthonormal product basis $\left\{ {\left| {\downarrow \downarrow } \right\rangle ,\left| {\downarrow \uparrow } \right\rangle ,\left| {\uparrow \downarrow } \right\rangle ,\left| {\uparrow \uparrow } \right\rangle } \right\}$, the state $\rho$ can be rewritten in the matrix form

$$\begin{aligned} \rho =\frac{1}{1+\left( {g+\sqrt{1+g^{2}}} \right) ^{2}}\left[ {{\begin{array}{cccc} {\left( {g+\sqrt{1+g^{2}}} \right) ^{2}}&{}\quad 0&{}\quad 0&{}\quad {g+\sqrt{1+g^{2}}} \\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ {g+\sqrt{1+g^{2}}}&{}\quad 0&{}\quad 0&{}\quad 1 \\ \end{array} }} \right] .\qquad \end{aligned}$$

(A10)

Then, the reduced density matrices $\rho _k$ for the subsystem k are

$$\begin{aligned} \rho _1 =\rho _2 =\frac{1}{1+\left( {g+\sqrt{1+g^{2}}} \right) ^{2}}\left[ {{\begin{array}{cc} {\left( {g+\sqrt{1+g^{2}}} \right) ^{2}}&{}\quad 0 \\ 0&{}\quad 1 \\ \end{array} }} \right] . \end{aligned}$$

(A11)

Correspondingly,

$$\begin{aligned} \rho _1^2 =\rho _2^2 =\frac{1}{\left[ {1+\left( {g+\sqrt{1+g^{2}}} \right) ^{2}} \right] ^{2}}\left[ {{\begin{array}{cc} {\left( {g+\sqrt{1+g^{2}}} \right) ^{4}}&{}\quad 0 \\ 0&{}\quad 1 \\ \end{array} }} \right] . \end{aligned}$$

(A12)

Based on Eq. (A12), we can readily calculate the global entanglement.