Skip to main content

Advertisement

Springer Nature Link
Log in

Public-key quantum digital signature scheme with one-time pad private-key

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

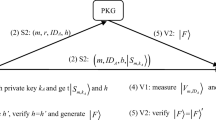
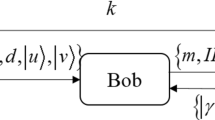
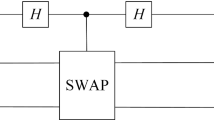
A quantum digital signature scheme is firstly proposed based on public-key quantum cryptosystem. In the scheme, the verification public-key is derived from the signer’s identity information (such as e-mail) on the foundation of identity-based encryption, and the signature private-key is generated by one-time pad (OTP) protocol. The public-key and private-key pair belongs to classical bits, but the signature cipher belongs to quantum qubits. After the signer announces the public-key and generates the final quantum signature, each verifier can verify publicly whether the signature is valid or not with the public-key and quantum digital digest. Analysis results show that the proposed scheme satisfies non-repudiation and unforgeability. Information-theoretic security of the scheme is ensured by quantum indistinguishability mechanics and OTP protocol. Based on the public-key cryptosystem, the proposed scheme is easier to be realized compared with other quantum signature schemes under current technical conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Okamoto, T., Tanaka, K., Uchiyama, S.: Quantum public-key cryptosystems. In: Bellare, M. (ed.) Advances in Cryptology–CRYPTO 2000. LNCS, vol. 1880, pp. 147–165. Springer, Berlin (2000)

  2. Nikolopoulos, G.M.: Applications of single-qubit rotations in quantum public-key cryptography. Phys. Rev. A 77(3), 032348 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  3. Seyfarth, U., Nikolopoulos, G.M., Alber, G.: Symmetries and security of a quantum-public-key encryption based on single-qubit rotations. Phys. Rev. A 85(2), 022342 (2012)

    Article  ADS  Google Scholar 

  4. Yang, L., Liang, M., Li, B., Hu, L., Feng, D. G.: Quantum public-key cryptosystems based on induced trapdoor one-way transformations. arXiv:quant-ph/1012.5249 (2011)

  5. Pan, J., Yang, L.: Quantum public-key encryption with information theoretic security. In: Proceedings of SPIE—The International Society for Optical Engineering, p. 8440 (2012)

  6. Yang, L., Yang, B., Xiang, C.: Quantum public-key encryption schemes based on conjugate coding. arXiv:quant-ph/1112.0421 (2013)

  7. Li, X.Y., Zhang, D.: Quantum public-key cryptosystem based on super dense coding technology. J. Comput. 8(12), 3168 (2013)

    Google Scholar 

  8. Gottesman, D., Chuang, I.: Quantum digital signatures. arXiv:quant-ph/0105032 (2001)

  9. Lamport, L.: Constructing digital signatures from a one-way function. In: Technical Report CSL-98, SRI International (1979)

  10. Zeng, G.H., Keitel, C.H.: Arbitrated quantum-signature scheme. Phys. Rev. A 65(4), 042312 (2002)

    Article  ADS  Google Scholar 

  11. Lee, H., Hong, C.H., Kim, H., Lim, J., Yang, H.J.: Arbitrated quantum signature scheme with message recovery. Phys. Lett. A 321(5), 295–300 (2004)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  12. Lu, X., Feng, D.G.: An arbitrated quantum message signature scheme. In: Lecture Notes in Computer Science, Vol. 3314, pp. 1054–1060. Springer, Berlin (2004)

  13. Lu, X., Feng, D.G.: Quantum digital signature based on quantum one-way functions. In: The International Conference on Advanced Communication Technology, Vol. 1, pp. 514–517. IEEE (2004)

  14. Yang, Y.G., Wen, Q.Y.: Arbitrated quantum signature of classical messages against collective amplitude damping noise. Opt. Commun. 283(16), 3198–3201 (2010)

    Article  ADS  Google Scholar 

  15. Yang, Y.G., Wen, Q.Y.: Erratum: arbitrated quantum signature of classical messages against collective amplitude damping noise. Opt. Commun. 283(19), 3830 (2010)

    Article  ADS  Google Scholar 

  16. Luo, Y.P., Hwang, T.: Arbitrated quantum signature of classical messages without using authenticated classical channels. Quantum Inf. Process. 13(1), 113–120 (2013)

    Article  ADS  Google Scholar 

  17. Li, Q., Li, C., Wen, Z., Zhao, W., Chan, W.H.: On the security of arbitrated quantum signature schemes. J. Phys. A-Math. Theor. 46(1), 015307 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. Dunjko, V., Wallden, P., Andersson, E.: Quantum digital signatures without quantum memory. Phys. Rev. Lett. 112(4), 040502 (2014)

    Article  ADS  Google Scholar 

  19. Collins, R.J., Donaldson, R.J., Dunjko, V., Wallden, P., Clarke, P.J., Andersson, E., et al.: Realization of quantum digital signatures without the requirement of quantum memory. Phys. Rev. Lett. 113(4), 040502 (2014)

    Article  ADS  Google Scholar 

  20. Amiri, R., Wallden, P., Kent, A., Andersson, E.: Secure quantum signatures using insecure quantum channels. Phys. Rev. A 93(3), 032325 (2016)

    Article  ADS  Google Scholar 

  21. Shamir, A.: Identity-Based Cryptosystems and Signature Schemes. In: The Workshop on the Theory and Application of Cryptographic Techniques, Vol. 21, pp. 47–53. Springer, Berlin Heidelberg (1984)

  22. Boneh, D., Franklin, M.: Identity based encryption from the weil pairing. SIAM J. Comput. 32(3), 213–229 (2001)

    MathSciNet  MATH  Google Scholar 

  23. Shannon, C.E.: Communication theory of secrecy systems. Bell Syst. Tech. J. 28, 656–715 (1949)

    Article  MathSciNet  MATH  Google Scholar 

  24. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information, pp. 531–536. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  25. Boykin, P.O., Roychowdhury, V.: Optimal encryption of quantum bits. Phys. Rev. A 67(4), 042317 (2003)

    Article  ADS  Google Scholar 

  26. Zhou, N.Y., Liu, Y., Zeng, G.H., Xiong, J., Zhou, F.C.: Novel qubit block encryption algorithm with hybrid keys. Phys. A 375(2), 693–698 (2007)

    Article  Google Scholar 

  27. Buhrman, H., Cleve, R., Watrous, J., de Wolf, R.: Quantum fingerprinting. Phys. Rev. Lett. 87(16), 167902 (2001)

    Article  ADS  Google Scholar 

  28. Menezes, A.J., Oorschot, P.V., Vanstone, S.A.: Handbook of Applied Cryptography. CRC Press, Boca Raton (1996)

    Book  MATH  Google Scholar 

  29. Goldreich, O.: Foundations of Cryptography: Basic Applications. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  30. Pan, J., Yang, L.: Quantum public-key encryption with information theoretic security. In: Proceedings of SPIE—The International Society for Optical Engineering, p. 8440 (2010)

  31. Yang, L., Xiang, C., Li, B.: Quantum probabilistic encryption scheme based on conjugate coding. China Commun. 10(2), 19–26 (2013)

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the Natural Science Foundation of the Education Department of Anhui Province (Grant Nos. KJ2015A266, KJ2014A144), National Natural Science Foundation of China (Grant No. 61702012) and University Outstanding Young Talent Support Project of Anhui Province of China (Grant No. gxyq2017026).

Author information

Authors and Affiliations

  1. School of Mathematics and Computation Science, AnQing Normal University, Anqing, 246011, China

    Feng-Lin Chen, Su-Gen Chen & Zhi-Hua Wang

  2. School of Physics and Electric Engineering, AnQing Normal University, Anqing, 246011, China

    Wan-Fang Liu

  3. School of Mathematical Sciences, University of Science and Technology of China, Hefei, 230026, China

    Zhi-Hua Wang

Authors
  1. Feng-Lin Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Wan-Fang Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Su-Gen Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Zhi-Hua Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Feng-Lin Chen.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, FL., Liu, WF., Chen, SG. et al. Public-key quantum digital signature scheme with one-time pad private-key. Quantum Inf Process 17, 10 (2018). https://doi.org/10.1007/s11128-017-1778-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-017-1778-5

Keywords