Violation of Bell inequalities for arbitrary-dimensional bipartite systems

Abstract

In this paper, we consider the violation of Bell inequalities for quantum system $\mathbb {C}^K\otimes \mathbb {C}^K$ (integer $K\ge 2$) with group theoretical method. For general M possible measurements, and each measurement with K outcomes, the Bell inequalities based on the choice of two orbits are derived. When the observables are much enough, the quantum bounds are only dependent on M and approximate to the classical bounds. Moreover, the corresponding nonlocal games with two different scenarios are analyzed.

Appendices

Appendix 1

Below we give the explicit calculation procedure of $\lambda _{\max }^O$ (4), the largest eigenvalue of O (3).

To be connivent, we choose

$$\begin{aligned} U= & {} | w_0 \rangle \langle w_0|+e^{-i2\pi /MK} | w_1 \rangle \langle w_1|+e^{-i4\pi /MK} | w_2 \rangle \langle w_2| \nonumber \\&+ \cdots + e^{i4\pi /MK} | w_{K-2} \rangle \langle w_{K-2}|+ e^{i2\pi /MK} | w_{K-1} \rangle \langle w_{K-1}|. \end{aligned}$$

(8)

Note that the eigenstates of $U\otimes U$ are states of the form $\left| \left. w_kw_l\right\rangle \right.$ for $k,l=0,1,2,\ldots , K-1$, and all eigenvalues are degenerate. There is a spectral decomposition for $U\otimes U$,

$$\begin{aligned} U\otimes U= \sum _\lambda \lambda P_\lambda , \end{aligned}$$

(9)

where $P_\lambda$ is the projector onto the eigenspace of $U\otimes U$ with eigenvalue $\lambda$, and $P_\lambda$ satisfy properties $\sum _\lambda P_\lambda =Id$ and $P_\lambda P_{\lambda '} =\delta _{\lambda \lambda '}P_\lambda$. Thus, the operator O can be simplified as follows:

$$\begin{aligned} O= & {} \sum _{j=0}^{MK-1}(U\otimes U)^j\left( \left| \left. 0v_1^0\right\rangle \right. \left. \left\langle 0v_1^0\right. \right| +\left| \left. 0v_1^1\right\rangle \right. \left. \left\langle 0v_1^1\right. \right| \right) (U^{\dag }\otimes U^{\dag })^j \nonumber \\= & {} \sum _{j=0}^{MK-1}\left( \sum _\lambda \lambda P_\lambda \right) ^j\left( \left| \left. 0v_1^0\right\rangle \right. \left. \left\langle 0v_1^0\right. \right| +\left| \left. 0v_1^1\right\rangle \right. \left. \left\langle 0v_1^1\right. \right| \right) \left( \sum _{\lambda '} \lambda '^* P_{\lambda '} ^{\dag }\right) ^j \nonumber \\= & {} MK\sum _\lambda P_\lambda \left( \left| \left. 0v_1^0\right\rangle \right. \left. \left\langle 0v_1^0\right. \right| +\left| \left. 0v_1^1\right\rangle \right. \left. \left\langle 0v_1^1\right. \right| \right) P_{\lambda }. \end{aligned}$$

(10)

Denote by $L(\lambda )$ the subspace spanned by all eigenvectors $\{u_\lambda ^{\lambda _j} \}$ of $U\otimes U$ corresponding to the eigenvalue $\lambda$. Then the eigenvector corresponding to the largest eigenvalue of O lies in the subspace $P_\lambda (\left| \left. 0v_1^0\right\rangle \right. \left. \left\langle 0v_1^0\right. \right| +\left| \left. 0v_1^1\right\rangle \right. \left. \left\langle 0v_1^1\right. \right| ) P_{\lambda }$ when $L(\lambda )$ has maximal dimension.

The case I

If integer $K>1$ is odd, the eigenvector corresponding to the largest eigenvalue of O lies in the subspace $P_1$. The eigenvectors of $U\otimes U$ corresponding to eigenvalue 1 are as follows:

$$\begin{aligned} \begin{array}{ccccc} |w_1w_{K-1} \rangle , &{} |w_2w_{K-2} \rangle , &{} \ldots &{} |w_{\frac{K-1}{2}}w_{\frac{K+1}{2}} \rangle , &{} |w_0w_0 \rangle ,\\ |w_{K-1}w_1 \rangle , &{} |w_{K-2}w_2 \rangle , &{} \ldots &{} |w_{\frac{K+1}{2}}w_{\frac{K-1}{2}} \rangle . &{} \end{array} \end{aligned}$$

Denote

$$\begin{aligned} R=P_{1}\left( \left| \left. 0v_1^0\right\rangle \right. \left. \left\langle 0v_1^0\right. \right| +\left| \left. 0v_1^1\right\rangle \right. \left. \left\langle 0v_1^1\right. \right| \right) P_{1}, \quad \left| \left. \psi _1\right\rangle \right. =P_{1}\left| \left. 0v_1^0\right\rangle \right. , \quad \left| \left. \psi _2\right\rangle \right. =P_{1}\left| \left. 0v_1^1\right\rangle \right. .\nonumber \\ \end{aligned}$$

(11)

Suppose that the eigenvectors of R corresponding to eigenvalue $\mu$ are $\sum _{j=1}^{2}x_j\left| \left. \psi _j\right\rangle \right.$, then the eigenvalue equation implies that $\sum _{j=1}^{2}x_j\langle \psi _k | \psi _j\rangle =\mu x_k$. Set the matrix

$$\begin{aligned} \Omega =\left[ \begin{array}{cc} \langle \psi _1 | \psi _1\rangle &{}\quad \langle \psi _1 | \psi _2\rangle \\ \langle \psi _2 | \psi _1\rangle &{}\quad \langle \psi _2 | \psi _2\rangle \\ \end{array} \right] , \end{aligned}$$

then we have

$$\begin{aligned} \Omega \left[ \begin{array}{c} x_1 \\ x_2\\ \end{array} \right] =\mu \left[ \begin{array}{c} x_1 \\ x_2\\ \end{array} \right] . \end{aligned}$$

The eigenvalues of $\Omega$ are exactly the ones of R. For $j=0,\ 1$, since

$$\begin{aligned} \left| \left. v_1^j\right\rangle \right.= & {} \frac{1}{\sqrt{K}}\left( \left| \left. w_0\right\rangle \right. +e^{-\frac{i\pi 2(M+j)}{MK}}\left| \left. w_1\right\rangle \right. +e^{-\frac{i\pi 4(M+j)}{MK}}\left| \left. w_2\right\rangle \right. +\cdots \right. \\&\left. +\,e^{\frac{i\pi 4(M+j)}{MK}}\left| \left. w_{K-2}\right\rangle \right. +e^{\frac{i\pi 2(M+j)}{MK}}\left| \left. w_{K-1}\right\rangle \right. \right) , \end{aligned}$$

it implies that

$$\begin{aligned} \left| \left. \mu _1\right\rangle \right.= & {} P_1\left| \left. 0v_1^0\right\rangle \right. =\frac{1}{K}\left( \left| \left. w_0w_0\right\rangle \right. +e^{\frac{i\pi 2}{K}}\left| \left. w_1w_{K-1}\right\rangle \right. +e^{-\frac{i\pi 2}{K}}\left| \left. w_{K-1}w_1\right\rangle \right. +e^{\frac{i\pi 4}{K}}\left| \left. w_2w_{K-2}\right\rangle \right. \right. \\&\left. +\,e^{\frac{-i\pi 4}{K}}\left| \left. w_{K-2}w_2\right\rangle \right. +\cdots +e^{\frac{i\pi (K-1)}{K}}|w_{\frac{K-1}{2}}w_{\frac{K+1}{2}}\rangle + e^{-\frac{i\pi (K-1)}{K}}|w_{\frac{K+1}{2}}w_{\frac{K-1}{2}}\rangle \right) , \end{aligned}$$

and

$$\begin{aligned} \left| \left. \mu _2\right\rangle \right.= & {} P_1\left| \left. 0v_1^1\right\rangle \right. =\frac{1}{K}(\left| \left. w_0w_0\right\rangle \right. +e^{\frac{i\pi 2(M+1)}{MK}}\left| \left. w_1w_{K-1}\right\rangle \right. +e^{-\frac{i\pi 2(M+1)}{MK}}\left| \left. w_{K-1}w_1\right\rangle \right. \\&+\,e^{\frac{i\pi 4(M+1)}{MK}}\left| \left. w_2w_{K-2}\right\rangle \right. +e^{-\frac{i\pi 4(M+1)}{MK}}\left| \left. w_{K-2}w_2\right\rangle \right. +\cdots \\&+\,e^{\frac{i\pi (K-1)(M+1)}{MK}}|w_{\frac{K-1}{2}}w_{\frac{K+1}{2}}\rangle + e^{-\frac{i\pi (K-1)(M+1)}{MK}}|w_{\frac{K+1}{2}}w_{\frac{K-1}{2}}\rangle ). \end{aligned}$$

Thus, $\langle \mu _1|\mu _1 \rangle =\langle \mu _2|\mu _2 \rangle =\frac{1}{K}$,

$$\begin{aligned} \langle \mu _1|\mu _2\rangle= & {} \frac{1}{K^2}\left( 1+e^{\frac{i\pi 2}{MK}}+e^{-\frac{i\pi 2}{MK}}+e^{\frac{i\pi 4}{MK}} +e^{-\frac{i\pi 4}{MK}}+\cdots +e^{\frac{i\pi (K-1)}{MK}}+e^{-\frac{i\pi (K-1)}{MK}}\right) \\= & {} \frac{1}{K^2}\left( 1+\cos \frac{(M-2)\pi }{2M}\csc \frac{\pi }{MK}- \cos \frac{(MK-2)\pi }{2MK}\csc \frac{\pi }{MK}\right) \\= & {} \frac{1}{K^2}\sin \frac{\pi }{M}\csc \frac{\pi }{MK}=\langle \mu _2|\mu _1\rangle . \end{aligned}$$

The largest eigenvalue of $\Omega$ is $(K+\sin \frac{\pi }{M}\csc \frac{\pi }{MK})/K^2$. Thus, the largest eigenvalue $\lambda _{\max }^O$ of O is

$$\begin{aligned} \lambda _{\max }^O= M\left( K+\sin \frac{\pi }{M}\csc \frac{\pi }{MK}\right) /K. \end{aligned}$$

The case II

If integer $K>1$ is even, the eigenvector corresponding to the largest eigenvalue of O lies in the subspace $P_{e^{i2\pi /MK}}$. The eigenvectors of $U\otimes U$ corresponding to eigenvalue $e^{i2\pi /MK}$ are as follows:

$$\begin{aligned} \begin{array}{ccccc} |w_0w_{K-1} \rangle , &{} |w_1w_{K-2} \rangle , &{} \ldots &{} |w_{\frac{K-2}{2}}w_{\frac{K}{2}} \rangle , \\ |w_{K-1}w_0 \rangle , &{} |w_{K-2}w_1 \rangle , &{} \ldots &{} |w_{\frac{K}{2}}w_{\frac{K-2}{2}} \rangle . &{} \end{array} \end{aligned}$$

The calculation procedure is similar to Case I. Although the form of matrix $\Omega$ is different,

$$\begin{aligned} \Omega =\left[ \begin{array}{cc} \frac{1}{K} &{}\quad \frac{1}{K^2} \left( \sin \frac{(K-1)\pi }{MK}\csc \frac{\pi }{MK}+e^{i\pi /M}\right) \\ \frac{1}{K^2} (\sin \frac{(K-1)\pi }{MK}\csc \frac{\pi }{MK}+e^{-i\pi /M}) &{}\quad \frac{1}{K} \\ \end{array} \right] , \end{aligned}$$

we have same the result of eigenvalues of $\Omega$. Hence, for any integer K, the largest eigenvalue $\lambda _{\max }^O$ of O is

$$\begin{aligned} \lambda _{\max }^O=M\left( K+\sin \frac{\pi }{M}\csc \frac{\pi }{MK}\right) \Big /K. \end{aligned}$$

Appendix 2

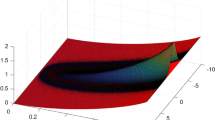
Below we show that the quantum bounds $\lambda _{\max }^O$ (4) only depend on M when M is large enough.

The partial derivative of function f(x, y) with respect to y is as follows:

$$\begin{aligned} \frac{\partial f(x,y) }{\partial y}=\csc (\pi x y) \sin (\pi x) - \pi x y \cot (\pi x y) \csc (\pi x y)\sin (\pi x), \end{aligned}$$

(12)

which always exceeds 0. Thus, the continuous function f(x, y) is a monotonic increasing function for any fixed x.

For the functions

$$\begin{aligned} f\left( x,\frac{1}{2}\right) = 1+\cos \frac{ \pi x}{2} \quad {\text{ a }nd } \quad f(x,0) := \lim _{y\rightarrow 0}f(x,y)= 1+\frac{1}{\pi x}\sin (\pi x), \end{aligned}$$

we draw the graphs of functions $f(x,\frac{1}{2})$ and f(x, 0) in Fig. 2, function $f(x,\frac{1}{2})$ is solid, and function f(x, 0) is dotted. From Fig. 2, we see that when x is near to 0, f(x, 0) approaches $f(x,\frac{1}{2})$.

Fig. 2

Graphs of f(x, 0) and $f(x,\frac{1}{2})$

That is to say, when the number of measurements is large enough, the violation of Bell inequality is determined by the number of measurements M and independent of K, the number of outcomes.