Skip to main content

Advertisement

Springer Nature Link
Log in

Improved quantum circuit modelling based on Heisenberg representation

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

Heisenberg model allows a more compact representation of certain quantum states and enables efficient modelling of stabilizer gates operation and single-qubit measurement in computational basis on classical computers. Since generic quantum circuit modelling appears intractable on classical computers, the Heisenberg representation that makes the modelling process at least practical for certain circuits is crucial. This paper proposes efficient algorithms to facilitate accurate global phase maintenance for both stabilizer and non-stabilizer gates application that play a vital role in the stabilizer frames data structure, which is based on the Heisenberg representation. The proposed algorithms are critical as maintaining global phase involves compute-intensive operations that are necessary for the modelling of each quantum gate. In addition, the proposed work overcomes the limitations of prior work where the phase factors due to non-stabilizer gates application was not taken into consideration. The verification of the proposed algorithms is made against the golden reference model that is constructed based on the conventional state vector approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Notes

  1. The terms Heisenberg model and stabilizer formalism are used interchangeably in this paper.

  2. Global phase is important in quantum mechanics when the differences in phase factors between two interacting quantum states are measurable [21].

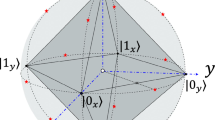
  3. A three-dimensional sphere of radius 1 that provides a way of visualizing a single-qubit state.

  4. Recall that the eigenvalue \(\lambda \) and eigenvector v of an n-by-n square matrix A are defined as \(Av = \lambda v\).

  5. The complexities stated in the caption of Algorithms 2–4 are for the computation of a complete set of N basis amplitudes. In the case of global phase maintenance, it only requires to obtain the amplitude of one or more basis indexes depending on the quantum gate type, regardless of the qubit size of the quantum circuit.

References

  1. Aaronson, S., Gottesman, D.: Improved simulation of stabilizer circuits. Phys. Rev. A 70(5), 052,328 (2004)

    Article  Google Scholar 

  2. Abubakar, M.Y., Jung, L.T., Zakaria, M.N., Younesy, A., Abdel-Atyz, A.H.: New universal gate library for synthesizing reversible logic circuit using genetic programming. In: International Conference on Computer and Information Sciences (ICCOINS), pp. 316–321. IEEE (2016)

  3. Abubakar, M.Y., Jung, L.T., Zakaria, N., Younes, A., Abdel-Aty, A.H.: Reversible circuit synthesis by genetic programming using dynamic gate libraries. Quantum Inf. Process. 16(6), 160 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. Barenco, A., Deutsch, D., Ekert, A., Jozsa, R.: Conditional quantum dynamics and logic gates. Phys. Rev. Lett. 74(20), 4083 (1995)

    Article  ADS  Google Scholar 

  5. Bennink, R.S., Ferragut, E.M., Humble, T.S., Laska, J.A., Nutaro, J.J., Pleszkoch, M.G., Pooser, R.C.: Unbiased simulation of near-Clifford quantum circuits. Phys. Rev. A 95(6), 062,337 (2017)

    Article  MathSciNet  Google Scholar 

  6. Bravyi, S., Gosset, D.: Improved classical simulation of quantum circuits dominated by Clifford gates. Phys. Rev. Lett. 116(25), 250,501 (2016)

    Article  Google Scholar 

  7. García, H.J., Markov, I.L.: Simulation of quantum circuits via stabilizer frames. IEEE Trans. Comput. 64(8), 2323–2336 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  8. García-Ramírez, H.J.: Hybrid techniques for simulating quantum circuits using the Heisenberg representation. Ph.D. thesis, The University of Michigan (2014)

  9. Gershenfeld, N.A., Chuang, I.L.: Bulk spin-resonance quantum computation. Science 275(5298), 350–356 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  10. Gottesman, D.: Stabilizer codes and quantum error correction. Ph.D. thesis, California Institute of Technology (1997)

  11. Gottesman, D.: The Heisenberg representation of quantum computers. arXiv:quant-ph/9807006 (1998)

  12. Homid, A., Abdel-Aty, A., Abdel-Aty, M., Badawi, A., Obada, A.S.: Efficient realization of quantum search algorithm using quantum annealing processor with dissipation. JOSA B 32(9), 2025–2033 (2015)

    Article  ADS  Google Scholar 

  13. Johansson, N., Larsson, J.Å.: Efficient classical simulation of the Deutsch–Jozsa and Simons algorithms. Quantum Inf. Process. 16(9), 233 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  14. Khalid, A.U., Zilic, Z., Radecka, K.: FPGA emulation of quantum circuits. In: IEEE International Conference on Computer Design: VLSI in Computers and Processors. ICCD 2004, pp. 310–315. IEEE (2004)

  15. Khalil-Hani, M., Lee, Y.H., Marsono, M.N.: An accurate FPGA-based hardware emulation on quantum fourier transform. In: Australasian Symposium on Parallel and Distributed Computing (AusPDC), vol. 1, p. a1b3 (2015)

  16. Kliuchnikov, V., Maslov, D.: Optimization of Clifford circuits. Phys. Rev. A 88(5), 052,307 (2013)

    Article  Google Scholar 

  17. Kliuchnikov, V., Maslov, D., Mosca, M.: Asymptotically optimal approximation of single qubit unitaries by Clifford and T circuits using a constant number of ancillary qubits. Phys. Rev. Lett. 110(19), 190,502 (2013)

    Article  Google Scholar 

  18. Knill, E., Leibfried, D., Reichle, R., Britton, J., Blakestad, R., Jost, J., Langer, C., Ozeri, R., Seidelin, S., Wineland, D.: Randomized benchmarking of quantum gates. Phys. Rev. A 77(1), 012,307 (2008)

    Article  MATH  Google Scholar 

  19. Lee, Y.H.: QCM: Quantum circuit modelling using state vector and Heisenberg representations. https://github.com/yeehui1988/QCM (2017)

  20. Lee, Y.H., Khalil-Hani, M., Marsono, M.N.: An FPGA-based quantum computing emulation framework based on serial-parallel architecture. Int. J. Reconfigurable Comput. 2016, 1–18 (2016)

  21. Messiah, A.: Quantum Mechanics. Dover Publications, New York (1999)

    MATH  Google Scholar 

  22. Miller, D.M., Thornton, M.A.: QMDD: a decision diagram structure for reversible and quantum circuits. In: 36th International Symposium on Multiple-Valued Logic, pp. 30–30. IEEE (2006)

  23. Monroe, C., Meekhof, D., King, B., Itano, W., Wineland, D.: Demonstration of a fundamental quantum logic gate. Phys. Rev. Lett. 75(25), 4714 (1995)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. Mooij, J., Orlando, T., Levitov, L., Tian, L., Van der Wal, C.H., Lloyd, S.: Josephson persistent-current qubit. Science 285(5430), 1036–1039 (1999)

    Article  Google Scholar 

  25. Muñoz-Coreas, E., Thapliyal, H.: Design of quantum circuits for galois field squaring and exponentiation. In: IEEE Computer Society Annual Symposium on VLSI (ISVLSI), pp. 68–73. IEEE (2017)

  26. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2010)

    Book  MATH  Google Scholar 

  27. Shiou-An, W., Chin-Yung, L., Sy-Yen, K., et al.: An XQDD-based verification method for quantum circuits. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 91(2), 584–594 (2008)

    Google Scholar 

  28. Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In: 35th Annual Symposium on Foundations of Computer Science, 1994 Proceedings, pp. 124–134. IEEE (1994)

  29. Simon, D.R.: On the power of quantum computation. SIAM J. Comput. 26(5), 1474–1483 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  30. Smelyanskiy, M., Sawaya, N.P., Aspuru-Guzik, A.: qHiPSTER: the quantum high performance software testing environment. arXiv:1601.07195 (2016)

  31. Viamontes, G.F., Markov, I.L., Hayes, J.P.: Improving QuIDD-based simulation. In: Quantum Circuit Simulation, pp. 133–152. Springer, Dordrecht (2009)

  32. Yanofsky, N.S., Mannucci, M.A.: Quantum Computing for Computer Scientists. Cambridge University Press, Cambridge (2008)

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Electrical and Information Engineering, The University of Sydney, Darlington, NSW, 2006, Australia

    Y. H. Lee

  2. VeCAD Research Laboratory, Faculty of Electrical Engineering, Universiti Teknologi Malaysia, 81310 UTM, Skudai, Johor Bahru, Malaysia

    M. Khalil-Hani & M. N. Marsono

Authors
  1. Y. H. Lee
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. M. Khalil-Hani
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. M. N. Marsono
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Y. H. Lee.

Additional information

This work is supported by the Ministry of Higher Education (MOHE) and Universiti Teknologi Malaysia (UTM) under Fundamental Research Grant Scheme (FRGS) Vote No. 4F422.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lee, Y.H., Khalil-Hani, M. & Marsono, M.N. Improved quantum circuit modelling based on Heisenberg representation. Quantum Inf Process 17, 36 (2018). https://doi.org/10.1007/s11128-017-1806-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-017-1806-5

Keywords