Heralded noiseless amplification for single-photon entangled state with polarization feature

Abstract

Heralded noiseless amplification is a promising method to overcome the transmission photon loss in practical noisy quantum channel and can effectively lengthen the quantum communication distance. Single-photon entanglement is an important resource in current quantum communications. Here, we construct two single-photon-assisted heralded noiseless amplification protocols for the single-photon two-mode entangled state and single-photon three-mode W state, respectively, where the single-photon qubit has an arbitrary unknown polarization feature. After the amplification, the fidelity of the single-photon entangled state can be increased, while the polarization feature of the single-photon qubit can be well remained. Both the two protocols only require the linear optical elements, so that they can be realized under current experimental condition. Our protocols may be useful in current and future quantum information processing.

Appendix

1.1 Amplification for single-photon two-mode entangled state

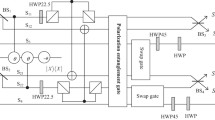
The schematic drawing of the amplification protocol is shown in Fig. 1. Due to the photon transmission loss, the single-photon two-mode entangled state degrades to a mixed state of

$$\begin{aligned} \rho _\mathrm{in}=\eta |\Phi \rangle _{AB}\langle \Phi |+(1-\eta )|vac\rangle \langle vac|. \end{aligned}$$

(19)

Here, $|\Phi \rangle _{AB}$ represents a single-photon two-mode entangled state, while the single-photon qubit has an arbitrary polarization feature. $|\Phi \rangle _{AB}$ can be written as

$$\begin{aligned} |\Phi \rangle _{AB}=\frac{1}{\sqrt{2}}(\alpha |H0\rangle _{a_{1}b_{1}}+\beta |V0\rangle _{a_{1}b_{1}}+\alpha |0H\rangle _{a_{1}b_{1}}+\beta |0V\rangle _{a_{1}b_{1}}). \end{aligned}$$

(20)

Here, $\alpha$ and $\beta$ meet $|\alpha |^{2}+|\beta |^{2}=1$.

We first consider that the single-photon qubit does not lose. By passing the single photon through a polarization beam splitter (PBS), which can fully transmit the photon in $|H\rangle$ and reflect the photon in $|V\rangle$, $|\Phi \rangle _{AB}$ evolves to

$$\begin{aligned} |\Phi _{1}\rangle= & {} \frac{1}{\sqrt{2}}\left( \alpha |H0\rangle _{a_{2}b_{2}}+\beta |V0\rangle _{a_{3}b_{3}}+\alpha |0H\rangle _{a_{2}b_{2}}+\beta |0V\rangle _{a_{3}b_{3}}\right) \nonumber \\= & {} \alpha |\Phi ^{+}\rangle _{a_{2}b_{2}}+\beta |\Phi ^{-}\rangle _{a_{3}b_{3}}, \end{aligned}$$

(21)

where

$$\begin{aligned} |\Phi ^{+}\rangle _{a_{2}b_{2}}= & {} \frac{1}{\sqrt{2}}\left( |H0\rangle _{a_{2}b_{2}}+|0H\rangle _{a_{2}b_{2}}\right) ,\nonumber \\ |\Phi ^{-}\rangle _{a_{3}b_{3}}= & {} \frac{1}{\sqrt{2}}\left( |V0\rangle _{a_{3}b_{3}}+|0V\rangle _{a_{3}b_{3}}\right) . \end{aligned}$$

(22)

Next, Alice and Bob make four single-photon sources $S_{2}\sim S_{5}$ emit four auxiliary photons. The two auxiliary photons in $a_{4}$ and $b_{4}$ modes are in $|H\rangle$, while the other two in $a_{7}$ and $b_{7}$ modes are in $|V\rangle$. It is noticed that single photons in $a_{2}a_{4}b_{2}b_{4}$ spatial modes should be indistinguishable, while the photons in $a_{3}a_{7}b_{3}b_{7}$ should be indistinguishable. Then, by making each of auxiliary photons pass through a variable beam splitter (VBS) with the transmittance of t, Alice and Bob can generate two auxiliary SPE states as

$$\begin{aligned} |\phi _{1}\rangle= & {} (\sqrt{1-t}|0H\rangle _{a_{5}a_{6}}+\sqrt{t}|H0\rangle _{a_{5}a_{6}})\otimes (\sqrt{1-t}|V0\rangle _{a_{8}a_{9}}+\sqrt{t}|0V\rangle _{a_{8}a_{9}}), \qquad \end{aligned}$$

(23)

$$\begin{aligned} |\phi _{2}\rangle= & {} (\sqrt{1-t}|0H\rangle _{b_{5}b_{6}}+\sqrt{t}|H0\rangle _{b_{5}b_{6}})\otimes (\sqrt{1-t}|V0\rangle _{b_{8}b_{9}}+\sqrt{t}|0V\rangle _{b_{8}b_{9}}).\qquad \end{aligned}$$

(24)

In this way, $|\Phi _{1}\rangle$ combined with the auxiliary photon states can be written as

$$\begin{aligned} |\Phi _{2}\rangle= & {} (\alpha |\Phi ^{+}\rangle _{a_{2}b_{2}}+\beta |\Phi ^{-}\rangle _{a_{3}b_{3}})\otimes |\phi _{1}\rangle \otimes |\phi _{2}\rangle \nonumber \\= & {} \alpha |\Phi ^{+}\rangle _{a_{2}b_{2}}\otimes |\phi _{1}\rangle \otimes |\phi _{2}\rangle +\beta |\Phi ^{-}\rangle _{a_{3}b_{3}}\otimes |\phi _{1}\rangle \otimes |\phi _{2}\rangle \nonumber \\= & {} \frac{1}{\sqrt{2}}\alpha [(1-t)|H00H0H\rangle +\sqrt{t(1-t)}|H00HH0\rangle +\sqrt{t(1-t)}|H0H00H\rangle \nonumber \\&+\,t|H0H0H0\rangle +(1-t)|0H0H0H\rangle +\sqrt{t(1-t)}|0H0HH0\rangle \nonumber \\&+\,\sqrt{t(1-t)}|0HH00H\rangle +\,t|0HH0H0\rangle ]_{a_{2}b_{2}a_{5}a_{6}b_{5}b_{6}}]\nonumber \\& \otimes [(1-t)|V0V0\rangle +\sqrt{t(1-t)}|V00V\rangle \nonumber \\&+\,\sqrt{t(1-t)}|0VV0\rangle +t|0V0V\rangle ]_{a_{8}a_{9}b_{8}b_{9}} +\frac{1}{\sqrt{2}}\beta [(1-t)|V0V0V0\rangle \nonumber \\&+\,\sqrt{t(1-t)}|V0V00V\rangle +\sqrt{t(1-t)}|V00VV0\rangle +t|V00V0V\rangle \nonumber \\&+\,(1-t)|0VV0V0\rangle +\sqrt{t(1-t)}|0VV00V\rangle \nonumber \\&+\,\sqrt{t(1-t)}|0V0VV0\rangle +t|0V0V0V\rangle ]_{a_{3}b_{3}a_{8}a_{9}b_{8}b_{9}}\otimes [(1-t)|0H0H\rangle \nonumber \\&+\,\sqrt{t(1-t)}|0HH0\rangle +\sqrt{t(1-t)}|H00H\rangle +t|H0H0\rangle ]_{a_{5}a_{6}b_{5}b_{6}}. \end{aligned}$$

(25)

Then, Alice and Bob make the photons in the $a_{2}a_{6}$, $a_{3}a_{8}$, $b_{2}b_{6}$, and $b_{3}b_{8}$ modes pass through four BSs, respectively, which

$$\begin{aligned} |1\rangle _{a_{2}}= & {} \frac{1}{\sqrt{2}}(|1\rangle _{d_{1}}+|1\rangle _{d_{2}}),\qquad |1\rangle _{a_{6}}=\frac{1}{\sqrt{2}}(|1\rangle _{d_{1}}-|1\rangle _{d_{2}}),\nonumber \\ |1\rangle _{a_{3}}= & {} \frac{1}{\sqrt{2}}(|1\rangle _{d_{3}}+|1\rangle _{d_{4}}),\qquad |1\rangle _{a_{8}}=\frac{1}{\sqrt{2}}(|1\rangle _{d_{3}}-|1\rangle _{d_{4}}).\nonumber \\ |1\rangle _{b_{2}}= & {} \frac{1}{\sqrt{2}}(|1\rangle _{d_{5}}+|1\rangle _{d_{6}}),\qquad |1\rangle _{b_{6}}=\frac{1}{\sqrt{2}}(|1\rangle _{d_{5}}-|1\rangle _{d_{6}}),\nonumber \\ |1\rangle _{b_{3}}= & {} \frac{1}{\sqrt{2}}(|1\rangle _{d_{7}}+|1\rangle _{d_{8}}),\qquad |1\rangle _{b_{8}}=\frac{1}{\sqrt{2}}(|1\rangle _{d_{7}}-|1\rangle _{d_{8}}). \end{aligned}$$

(26)

It can be found that if both the two input spatial modes of a BS contain a photon, after passing through the BS, the two photons will be both in either one of the two output modes. It is also called the Hong-Ou-Mandel (HOM) bunching effect. On the other hand, if only an input spatial mode of a BS contains a photon, the output photon will be in either of the two output modes. Alice and Bob select the cases where only one of the two output modes of each BS contains exactly one photon. After the BSs, the selected state in Eq. (25) will evolve to

$$\begin{aligned} |\Phi _{3}\rangle= & {} \frac{\alpha \sqrt{t(1-t)}}{2\sqrt{2}}[(|H\rangle _{d_{1}}+|H\rangle _{d_{2}})(|H\rangle _{d_{5}}-|H\rangle _{d_{6}})|H0\rangle _{a_{5}b_{5}}\nonumber \\&+\,(|H\rangle _{d_{1}}-|H\rangle _{d_{2}})(|H\rangle _{d_{5}}+|H\rangle _{d_{6}})|0H\rangle _{a_{5}b_{5}}]\nonumber \\&\otimes \frac{1-t}{2}(|V\rangle _{d_{3}}-|V\rangle _{d_{4}})(|V\rangle _{d_{7}}-|V\rangle _{d_{8}})\nonumber \\&+\,\frac{\beta \sqrt{t(1-t)}}{2\sqrt{2}}[(|V\rangle _{d_{3}}\nonumber \\&+\,|V\rangle _{d_{4}})(|V\rangle _{d_{7}}-|V\rangle _{d_{8}})|V0\rangle _{a_{9}b_{9}} +(|V\rangle _{d_{3}}-|V\rangle _{d_{4}})(|V\rangle _{d_{7}}+|V\rangle _{d_{8}})|0V\rangle _{a_{9}b_{9}}]\nonumber \\&\otimes \frac{1-t}{2}(|H\rangle _{d_{1}}-|H\rangle _{d_{2}})(|H\rangle _{d_{5}}-|H\rangle _{d_{6}}). \end{aligned}$$

(27)

Next, the photons in the eight output modes $d_{i}$ $(i=1, 2, \ldots , 8)$ are detected by the single-photon detectors $D_{i}$ $(i=1, 2, \ldots , 8)$, respectively. There are sixteen detection results corresponding to the successful cases of our protocol, which are shown in Table 1.

We take the detection result of $D_{1}D_{3}D_{5}D_{7}$ for an example. From Eq. (27), if $D_{1}D_{3}D_{5}D_{7}$ each registers a single photon, the parties will obtain the state as

$$\begin{aligned} |\Phi _{4}\rangle =\frac{\alpha }{\sqrt{2}}(|H0\rangle _{a_{5}b_{5}}+|0H\rangle _{a_{5}b_{5}}) +\frac{\beta }{\sqrt{2}}(|V0\rangle _{a_{9}b_{9}}+|0V\rangle _{a_{9}b_{9}}), \end{aligned}$$

(28)

with the probability of $\frac{ t(1-t)^{3}}{16}$.

If the parties obtain one of the other fifteen detection results shown in Table 1, they can also finally obtain $|\Phi _{4}\rangle$ with the help of the phase-flip operation. Therefore, under the case that the single photon does not lose, the success probability of our protocol is

$$\begin{aligned} P_{1}=\eta \frac{ t(1-t)^{3}}{16}\times 16=\eta t(1-t)^{3}. \end{aligned}$$

(29)

Finally, the parties make the photons in $a_{5}a_{9}$ and $b_{5}b_{9}$ modes enter PBS$_{2}$ and PBS$_{4}$, respectively. After the PBSs, they can obtain

$$\begin{aligned} |\Phi _{5}\rangle =\frac{1}{\sqrt{2}}(\alpha |H0\rangle _{a_{10}b_{10}}+\alpha |0H\rangle _{a_{10}b_{10}}+\beta |V0\rangle _{a_{10}b_{10}}+\beta |0V\rangle _{a_{10}b_{10}}) =|\Phi \rangle _{AB}.\nonumber \\ \end{aligned}$$

(30)

On the other hand, under the case that the photon is lost with the probability of $1-\eta$. Combined with the four auxiliary single photons, the whole photon state can be written as

$$\begin{aligned} |vac\rangle \otimes |\phi _{1}\rangle \otimes |\phi _{2}\rangle= & {} [(\sqrt{1-t}|0H\rangle _{a_{5}a_{6}}+\sqrt{t}|H0\rangle _{a_{5}a_{6}}) \otimes (\sqrt{1-t}|0H\rangle _{b_{5}b_{6}}\nonumber \\&\quad +\,\sqrt{t}|H0\rangle _{b_{5}b_{6}})]\nonumber \\&\otimes [(\sqrt{1-t}|V0\rangle _{a_{8}a_{9}}+\sqrt{t}|0V\rangle _{a_{8}a_{9}}) \otimes (\sqrt{1-t}|V0\rangle _{b_{8}b_{9}}\nonumber \\&\quad +\,\sqrt{t}|0V\rangle _{b_{8}b_{9}})]\nonumber \\= & {} [(1-t)|0H0H\rangle +\sqrt{t(1-t)}|0HH0\rangle +\sqrt{t(1-t)}|H00H\rangle \nonumber \\&\quad +\,t|H0H0\rangle ]_{a_{5}a_{6}b_{5}b_{6}}\nonumber \\&\otimes [(1-t)|V0V0\rangle +\sqrt{t(1-t)}|V00V\rangle +\sqrt{t(1-t)}|0VV0\rangle \nonumber \\&\quad +\,t|0V0V\rangle ]_{a_{8}a_{9}b_{8}b_{9}}. \end{aligned}$$

(31)

After making the photons in $a_{2}a_{6}$, $a_{3}a_{8}$, $b_{2}b_{6}$, and $b_{3}b_{8}$ modes pass through four BSs, respectively, and selecting one of the sixteen detection results shown in Table 1, the state in Eq. (31) will finally collapse to

$$\begin{aligned} |\Phi _{6}\rangle =(1-t)^{2}|vac\rangle , \end{aligned}$$

(32)

with the probability of $\frac{(1-t)^{4}}{16}$. In this way, the total success probability of our protocol corresponding to the initial vacuum state is

$$\begin{aligned} P_{2}=(1-\eta )\frac{(1-t)^{4}}{16}\times 16=(1-\eta )(1-t)^{4}. \end{aligned}$$

(33)

Therefore, for the initial mixed state $\rho _\mathrm{in}$, the total success probability of our protocol is

$$\begin{aligned} P=P_{1}+P_{2}=\eta t(1-t)^{3}+(1-\eta )(1-t)^{4}. \end{aligned}$$

(34)

After choosing the successful cases, the parties will finally obtain a new mixed state as

$$\begin{aligned} \rho _\mathrm{out}=\eta '|\Phi \rangle _{AB}\langle \Phi |+(1-\eta ')|vac\rangle \langle vac|. \end{aligned}$$

(35)

Here,

$$\begin{aligned} \eta '=\frac{\eta t(1-t)^{3}}{\eta t(1-t)^{3}+(1-\eta )(1-t)^{4}}=\frac{\eta t}{\eta t+(1-\eta )(1-t)}. \end{aligned}$$

(36)

We define the amplification factor G as $G=\frac{\eta '}{\eta }$. In this way, in our protocol, the amplification factor G is

$$\begin{aligned} G=\frac{\eta '}{\eta }=\frac{t}{\eta t+(1-\eta )(1-t)}. \end{aligned}$$

(37)

1.2 Amplification for single-photon three-mode W state

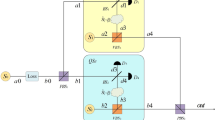
The schematic drawing of the amplification protocol is shown in Fig. 2. The initial input mixed state has the form of

$$\begin{aligned} \rho _{\mathrm{in}W}=\eta |\Psi \rangle _{ABC}\langle \Psi |+(1-\eta )|vac\rangle \langle vac|. \end{aligned}$$

(38)

Here, $|\Psi \rangle _{ABC}$ can be written as

$$\begin{aligned} |\Psi \rangle _{ABC}= & {} \frac{1}{\sqrt{3}}(\alpha |H00\rangle +\beta |V00\rangle +\alpha |0H0\rangle +\beta |0V0\rangle +\alpha |00H\rangle +\beta |00V\rangle )_{a_{1}b_{1}c_{1}}.\nonumber \\ \end{aligned}$$

(39)

As shown in Fig. 2, we also first consider the case that the single photon does not lose. Alice, Bob, and Charlie make the photon in the $a_{1}$, $b_{1}$, and $c_{1}$ modes pass through the PBS$_{1}$, PBS$_{3}$, and PBS$_{5}$, respectively. After that, $|\Psi \rangle _{ABC}$ will evolve to

$$\begin{aligned} |\Psi _{1}\rangle _{ABC}= & {} \frac{1}{\sqrt{3}}(\alpha |H00\rangle _{a_{2}b_{2}c_{2}}+\beta |V00\rangle _{a_{3}b_{3}c_{3}}+\alpha |0H0\rangle _{a_{2}b_{2}c_{2}}+\beta |0V0\rangle _{a_{3}b_{3}c_{3}}\nonumber \\&+\,\alpha |00H\rangle _{a_{2}b_{2}c_{2}}+\beta |00V\rangle _{a_{3}b_{3}c_{3}})\nonumber \\= & {} \alpha |\Psi _{1}^{+}\rangle _{a_{2}b_{2}c_{2}}+\beta |\Psi _{1}^{-}\rangle _{a_{3}b_{3}c_{3}}, \end{aligned}$$

(40)

where

$$\begin{aligned} |\Psi _{1}^{+}\rangle _{a_{2}b_{2}c_{2}}= & {} \frac{1}{\sqrt{3}}(|H00\rangle +|0H0\rangle +|00H\rangle )_{a_{2}b_{2}c_{2}},\nonumber \\ |\Psi _{1}^{-}\rangle _{a_{3}b_{3}c_{3}}= & {} \frac{1}{\sqrt{3}}(|V00\rangle +|0V0\rangle +|00V\rangle )_{a_{3}b_{3}c_{3}}. \end{aligned}$$

(41)

For realizing the amplification, each of the three parties should prepare two auxiliary photons. The photons in $a_{4}$, $b_{4}$, and $c_{4}$ modes are in $|H\rangle$, while those in $a_{7}$, $b_{7}$, and $c_{7}$ modes are in $|V\rangle$. Similarly, all the photons in $|H\rangle$ and all the photons in $|V\rangle$ should be indistinguishable. Then, the three parties pass each of the auxiliary single photons through a VBS with the transmittance of t. In this way, $|\Psi _{1}\rangle _{ABC}$ combined with the auxiliary photon states can be written as

$$\begin{aligned} |\Psi _{2}\rangle= & {} \frac{1}{\sqrt{3}}\alpha (|H00\rangle +|0H0\rangle +|00H\rangle )_{a_{2}b_{2}c_{2}} \otimes [(\sqrt{1-t}|0H\rangle +\sqrt{t}|H0\rangle )_{a_{5}a_{6}}\nonumber \\&\otimes (\sqrt{1-t}|0H\rangle +\sqrt{t}|H0\rangle )_{b_{5}b_{6}} \otimes (\sqrt{1-t}|0H\rangle +\sqrt{t}|H0\rangle )_{c_{5}c_{6}}]\nonumber \\&\otimes [(\sqrt{1-t}|V0\rangle +\sqrt{t}|0V\rangle )_{a_{8}a_{9}} \otimes (\sqrt{1-t}|V0\rangle +\sqrt{t}|0V\rangle )_{b_{8}b_{9}}\nonumber \\&\otimes (\sqrt{1-t}|V0\rangle +\sqrt{t}|0V\rangle )_{c_{8}c_{9}}] +\frac{1}{\sqrt{3}}\beta (|V00\rangle +|0V0\rangle +|00V\rangle )_{a_{3}b_{3}c_{3}}\nonumber \\&\otimes [(\sqrt{1-t}|0H\rangle +\sqrt{t}|H0\rangle )_{a_{5}a_{6}} \otimes (\sqrt{1-t}|0H\rangle +\sqrt{t}|H0\rangle )_{b_{5}b_{6}}\nonumber \\&\otimes (\sqrt{1-t}|0H\rangle +\sqrt{t}|H0\rangle )_{c_{5}c_{6}}]\nonumber \\&\otimes [(\sqrt{1-t}|V0\rangle +\sqrt{t}|0V\rangle )_{a_{8}a_{9}}\nonumber \\&\otimes (\sqrt{1-t}|V0\rangle +\sqrt{t}|0V\rangle )_{b_{8}b_{9}} \otimes (\sqrt{1-t}|V0\rangle +\sqrt{t}|0V\rangle )_{c_{8}c_{9}}]. \end{aligned}$$

(42)

After that, they make the photons in $a_{2}a_{6}$, $a_{3}a_{8}$, $b_{2}b_{6}$, $b_{3}b_{8}$, $c_{2}c_{6}$, and $c_{3}c_{8}$ modes enter BSs, respectively. Similar to the protocol in Sect. 2, the parties also select the items which make only one of the two output modes in each BS has exactly one photon. In this way, $|\Psi _{2}\rangle$ will finally evolve to

$$\begin{aligned} |\Psi _{3}\rangle= & {} \frac{1}{8\sqrt{3}}\alpha (1-t)^{2}\sqrt{t(1-t)}(|V\rangle _{d_{3}}-|V\rangle _{d_{4}}) (|V\rangle _{d_{7}}-|V\rangle _{d_{8}}) (|V\rangle _{d_{11}}-|V\rangle _{d_{12}})\nonumber \\&\otimes [(|H\rangle _{d_{1}}+|H\rangle _{d_{2}})(|H\rangle _{d_{5}}-|H\rangle _{d_{6}})(|H\rangle _{d_{9}}-|H\rangle _{d_{10}}) |H00\rangle _{a_{5}b_{5}c_{5}}\nonumber \\&\quad +\,(|H\rangle _{d_{1}}-|H\rangle _{d_{2}})(|H\rangle _{d_{5}}+|H\rangle _{d_{6}}) (|H\rangle _{d_{9}}-|H\rangle _{d_{10}}) |0H0\rangle _{a_{5}b_{5}c_{5}}\nonumber \\&\quad +\,(|H\rangle _{d_{1}}-|H\rangle _{d_{2}})(|H\rangle _{d_{5}}-|H\rangle _{d_{6}}) (|H\rangle _{d_{9}}+|H\rangle _{d_{10}}) |00H\rangle _{a_{5}b_{5}c_{5}}]\nonumber \\&\quad +\,\frac{1}{8\sqrt{3}}\beta (1-t)^{2}\sqrt{t(1-t)}(|H\rangle _{d_{1}}-|H\rangle _{d_{2}}) (|H\rangle _{d_{5}}-|H\rangle _{d_{6}}) (|H\rangle _{d_{9}}-|H\rangle _{d_{10}})\nonumber \\&\otimes [(|V\rangle _{d_{3}}+|V\rangle _{d_{4}})(|V\rangle _{d_{7}}-|V\rangle _{d_{8}})(|V\rangle _{d_{11}}-|V\rangle _{d_{12}}) |V00\rangle _{a_{9}b_{9}c_{9}}\nonumber \\&\quad +\,(|V\rangle _{d_{3}}-|V\rangle _{d_{4}})(|V\rangle _{d_{7}}+|V\rangle _{d_{8}})(|V\rangle _{d_{11}}-|V\rangle _{d_{12}}) |0V0\rangle _{a_{9}b_{9}c_{9}}\nonumber \\&\quad +\,(|V\rangle _{d_{3}}-|V\rangle _{d_{4}})(|V\rangle _{d_{7}}-|V\rangle _{d_{8}})(|V\rangle _{d_{11}}+|V\rangle _{d_{12}}) |00V\rangle _{a_{9}b_{9}c_{9}}] \end{aligned}$$

(43)

with the probability of $t(1-t)^{5}$.

Then, the photons in all the twelve output modes $d_{i}$ $(i=1, 2, \ldots , 12)$ are detected by the single-photon detectors $D_{i}$ $(i=1, 2, \ldots , 12)$, respectively. $|\Psi _{3}\rangle$ will cause Alice to obtain $D_{1}D_{3}$, $D_{1}D_{4}$, $D_{2}D_{3}$, or $D_{2}D_{4}$ each registering a single photon, Bob obtain $D_{5}D_{7}$, $D_{5}D_{8}$, $D_{6}D_{7}$, or $D_{6}D_{8}$ each registering a single photon, and Charlie obtain $D_{9}D_{11}$, $D_{9}D_{12}$, $D_{10}D_{11}$, or $D_{10}D_{12}$ each registering a single photon. Therefore, there are sixty-four successful detection results in total.

Here, we take the detection result of $D_{1}D_{3}D_{5}D_{7}D_{9}D_{11}$ each registering a single photon for example. Under this detection result, the state in Eq. (43) will evolve to

$$\begin{aligned} |\Psi _{4}\rangle _{ABC}=\frac{\alpha }{\sqrt{3}}(|H00\rangle +|0H0\rangle +|00H\rangle )_{a_{5}b_{5}c_{5}} +\frac{\beta }{\sqrt{3}}(|V00\rangle +|0V0\rangle +|00V\rangle )_{a_{9}b_{9}c_{9}}.\nonumber \\ \end{aligned}$$

(44)

If the parties obtain one of the other sixty-three successful detection results, they can finally obtain $|\Psi _{4}\rangle _{ABC}$ by the phase-flip operation.

Finally, the parties make the photons in $a_{5}a_{9}$, $b_{5}b_{9}$, and $c_{5}c_{9}$ modes enter PBS$_{2}$, PBS$_{4}$, and PBS$_{6}$, respectively. After the PBSs, $|\Psi _{4}\rangle _{ABC}$ will finally evolve to

$$\begin{aligned} |\Psi _{5}\rangle= & {} \frac{1}{\sqrt{3}}(\alpha |H00\rangle +\alpha |0H0\rangle +\alpha |00H\rangle +\beta |V00\rangle +\beta |0V0\rangle +\beta |00V\rangle )_{a_{10}b_{10}c_{10}}\nonumber \\= & {} \frac{1}{\sqrt{3}}(|\varphi 00\rangle +|0\varphi 0\rangle +|00\varphi \rangle )_{a_{10}b_{10}c_{10}}. \end{aligned}$$

(45)

Considering the single photon does not lose with the probability of $\eta$, the success probability of our protocol can be written as

$$\begin{aligned} P_{1W}=\eta t(1-t)^{5}. \end{aligned}$$

(46)

Next, we deal with the case that the photon is lost with the probability of $1-\eta$. Combined with the three auxiliary single photons in $|H\rangle$ and the three auxiliary single photons in $|V\rangle$, the whole photon state can be written as

$$\begin{aligned} |\Psi _{6}\rangle= & {} [(\sqrt{1-t}|0H\rangle +\sqrt{t}|H0\rangle )_{a_{5}a_{6}} \otimes (\sqrt{1-t}|0H\rangle +\sqrt{t}|H0\rangle )_{b_{5}b_{6}}\nonumber \\&\otimes (\sqrt{1-t}|0H\rangle +\sqrt{t}|H0\rangle )_{c_{5}c_{6}}] \otimes [(\sqrt{1-t}|V0\rangle +\sqrt{t}|0V\rangle )_{a_{8}a_{9}}\nonumber \\&\otimes (\sqrt{1-t}|V0\rangle +\sqrt{t}|0V\rangle )_{b_{8}b_{9}} \otimes (\sqrt{1-t}|V0\rangle +\sqrt{t}|0V\rangle )_{c_{8}c_{9}}]. \end{aligned}$$

(47)

After the whole above operation, only the item $|0H0H0HV0V0V0\rangle _{a_{5}a_{6}b_{5}b_{6}c_{5}c_{6}a_{8}a_{9}b_{8}b_{9}c_{8}c_{9}}$ will make the three parties obtain one of the above sixty-four successful detection results. In this way, the state in Eq. (47) will collapse to

$$\begin{aligned} |\Psi _{7}\rangle =(1-t)^{3}|0H0H0HV0V0V0\rangle _{a_{5}a_{6}b_{5}b_{6}c_{5}c_{6}a_{8}a_{9}b_{8}b_{9}c_{8}c_{9}}, \end{aligned}$$

(48)

with the probability of $(1-t)^{6}$. After the BSs, the output photons are detected by the single-photon detectors, and the photon state in Eq. (48) will finally evolve to the vacuum state.

Based on above description, the total success probability of our protocol corresponding to the initial vacuum state is

$$\begin{aligned} P_{2W}=(1-\eta )(1-t)^{6}. \end{aligned}$$

(49)

Therefore, for the initial mixed state $\rho _{\mathrm{in}W}$, the total success probability of our protocol is

$$\begin{aligned} P_{W}=P_{1W}+P_{2W}=\eta t(1-t)^{5}+(1-\eta )(1-t)^{6}. \end{aligned}$$

(50)

After choosing the success cases, the parties will finally obtain a new mixed state as

$$\begin{aligned} \rho _{\mathrm{out}W}=\eta '_{W}|\Psi \rangle _{ABC}\langle \Psi |+(1-\eta '_{W})|vac\rangle \langle vac|. \end{aligned}$$

(51)

Here,

$$\begin{aligned} \eta _{W}'=\frac{\eta t(1-t)^{5}}{\eta t(1-t)^{5}+(1-\eta )(1-t)^{6}}=\frac{\eta t}{\eta t+(1-\eta )(1-t)}. \end{aligned}$$

(52)

We also define the amplification factor $G_{W}$ as $G_{W}=\frac{\eta '}{\eta }$. In this way, in our protocol, the amplification factor G is

$$\begin{aligned} G_{W}=\frac{\eta _{W}'}{\eta }=\frac{t}{\eta t+(1-\eta )(1-t)}, \end{aligned}$$

(53)

which equals to the amplification factor for the single-photon two-mode entangled state.