Dynamics of tripartite quantum correlations and decoherence in flux qubit systems under local and non-local static noise

Abstract

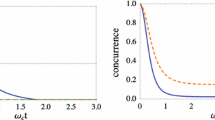
We investigate the dynamics of entanglement, decoherence and quantum discord in a system of three non-interacting superconducting flux qubits (fqubits) initially prepared in a Greenberger–Horne–Zeilinger (GHZ) state and subject to static noise in different, bipartite and common environments, since it is recognized that different noise configurations generally lead to completely different dynamical behavior of physical systems. The noise is modeled by randomizing the single fqubit transition amplitude. Decoherence and quantum correlations dynamics are strongly affected by the purity of the initial state, type of system–environment interaction and the system–environment coupling strength. Specifically, quantum correlations can persist when the fqubits are commonly coupled to a noise source, and reaches a saturation value respective to the purity of the initial state. As the number of decoherence channels increases (bipartite and different environments), decoherence becomes stronger against quantum correlations that decay faster, exhibiting sudden death and revival phenomena. The residual entanglement can be successfully detected by means of suitable entanglement witness, and we derive a necessary condition for entanglement detection related to the tunable and non-degenerated energy levels of fqubits. In accordance with the current literature, our results further suggest the efficiency of fqubits over ordinary ones, as far as the preservation of quantum correlations needed for quantum processing purposes is concerned.

Appendix: Explicit forms of the various density matrices

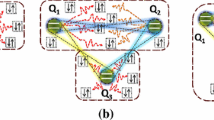
• Different environments coupling: For the case of local coupling to different environments with a static noise, we set $x_A \ne x_B \ne x_C$, and the density matrix for the global system at time t is derived from:

  $$\begin{aligned} {\rho _{de}}\left( t\right) =\int _{d^{-}}^{d^{+}}\int _{d^{-}}^ {d^{+}}\int _{d^{-}}^{d^{+}}{\hbox {d}{x_{A}}\hbox {d}{x_{B}}\hbox {d}{x_{C}}P\left( {x_{A}}\right) P\left( {x_{B}}\right) P\left( {x_{C}}\right) \rho \left( {{x_{A}},{x_{B}},{x_{C}},t}\right) }\nonumber \\ \end{aligned}$$

  (29)

  where $d^{\pm } = x_0 \pm \frac{{x_{m}}}{2}$ and $\rho \left( {{x_{A}},{x_{B}},{x_{C}},t}\right) ={U}\left( {{x_{A}},{x_{B}},{x_{C}},t}\right) \rho (0)U^{\dagger }({x_{A}},{x_{B}},{x_{C}},t).$ Explicitly, $\rho _{de}(t)$ reads:

  $$\begin{aligned} \rho _{de}(t)=\frac{1}{2}\begin{pmatrix} \alpha _{de} &{} \gamma _{de} &{} \gamma _{de} &{} \mu _{de} &{} \gamma _{de} &{} \mu _{de} &{} \mu _{de} &{} \alpha _{de}e^{6i\theta }\\ \gamma _{de}^{*} &{} \vartheta _{de} &{} \tau _{de} &{} \kappa _{de} &{} \tau _{de} &{} \kappa _{de} &{} \chi _{de} &{} \pi _{de}\\ \gamma _{de}^{*} &{} \tau _{de} &{} \vartheta _{de} &{} \kappa _{de} &{} \tau _{de} &{} \chi _{de} &{} \kappa _{de} &{} \pi _{de}\\ \mu _{de}^{*} &{} \kappa _{de}^{*} &{} \kappa _{de}^{*} &{} \vartheta _{de} &{} \chi _{de}^{*} &{} \tau _{de} &{} \tau _{de} &{} \varepsilon _{de}\\ \gamma _{de}^{*} &{} \tau _{de} &{} \tau _{de} &{} \chi _{de} &{} \vartheta _{de} &{} \kappa _{de} &{} \kappa _{de} &{} \pi _{de}\\ \mu _{de}^{*} &{} \kappa _{de}^{*} &{} \chi _{de}^{*} &{} \tau _{de} &{} \kappa _{de}^{*} &{} \vartheta _{de} &{} \tau _{de} &{} \varepsilon _{de}\\ \mu _{de}^{*} &{} \chi _{de}^{*} &{} \kappa _{de}^{*} &{} \tau _{de} &{} \kappa _{de}^{*} &{} \tau _{de} &{} \vartheta _{de} &{} \varepsilon _{de}\\ \alpha _{de}e^{-6i\theta } &{} \pi _{de}^{*} &{} \pi _{de}^{*} &{} \varepsilon _{de}^{*} &{} \pi _{de}^{*} &{} \varepsilon _{de}^{*} &{} \varepsilon _{de}^{*} &{} \alpha _{de} \end{pmatrix} \end{aligned}$$

  (30)

  where

  $$\begin{aligned} \alpha _{de}=\frac{1}{4}\left[ 1+3p\beta _{de}\cos ^{2}(\nu tx_{0})\right] ,\quad \tau _{de}=\frac{p}{4}\beta _{de}\sin ^{2}\left( \nu tx_{0}\right) ,\\ \pi _{de}=\frac{p}{4}e^{4i\theta }\beta _{de}\left[ i\sin (2\nu tx_{0})-\sin ^{2}(\nu tx_{0})\right] ,\quad \chi _{de}=\pi _{de}e^{2i\theta } \\ \gamma _{de}=-\frac{p}{4}e^{2i\theta }\beta _{de}\left[ \sin ^{2}(\nu tx_{0})+i\sin (2\nu tx_{0})\right] ,\quad \mu _{de}=\gamma _{de}e^{2i\theta } \\ \varepsilon _{de}=\frac{p}{4}e^{2i\theta }\beta _{de}\left[ -\sin ^{2}(\nu tx_{0})+i\sin (2\nu tx_{0})\right] ,\quad \kappa _{de}=\tau _{de}e^{2i\theta }\\ \vartheta _{de}=\frac{1}{4}\left[ 1-p\beta _{de}\cos ^{2}(\nu tx_{0})\right] ,\quad \beta _{de}=\left( \frac{2\sin \left( \nu tx_{m}/2\right) }{\nu tx_{m}}\right) ^{2} \end{aligned}$$

• Common environment coupling: Here we set $x_A = x_B = x_C = x$. The time-evolved state is derived from:

  $$\begin{aligned} {\rho _{ce}}\left( t\right) =\int _{d^{-}}^{d^{+}}{\hbox {d}{x} P\left( {x}\right) \rho \left( {{x},,t}\right) }, \end{aligned}$$

  (31)

  where $\rho \left( {{x},t}\right) ={U}\left( {{x},t}\right) \rho (0) U^{\dag }\left( {x,t}\right) ,$ and reads:

  $$\begin{aligned} \rho _{ce}(t)=\frac{1}{2}\begin{pmatrix}\alpha _{ce} &{} \,\,\gamma _{ce}\,\, &{} \,\,\gamma _{ce}\,\, &{} \,\,\mu _{ce}\,\, &{} \,\,\gamma _{ce}\,\, &{} \,\,\mu _{ce}\,\, &{} \,\,\mu _{ce}\,\, &{} \,\alpha _{ce}e^{6i\theta }\\ \gamma _{ce}^{*} &{} \vartheta _{ce} &{} \tau _{ce} &{} \chi _{ce} &{} \tau _{ce} &{} \chi _{ce} &{} \chi _{ce} &{} \pi _{ce}\\ \gamma _{ce}^{*} &{} \tau _{ce} &{} \vartheta _{ce} &{} \chi _{ce} &{} \tau _{ce} &{} \chi _{ce} &{} \chi _{ce} &{} \pi _{ce}\\ \mu _{ce}^{*} &{} \chi _{ce}^{*} &{} \chi _{ce}^{*} &{} \vartheta _{ce} &{} \chi _{ce}^{*} &{} \tau _{ce} &{} \tau _{ce} &{} \varepsilon _{ce}\\ \gamma _{ce}^{*} &{} \tau _{ce} &{} \tau _{ce} &{} \chi _{ce} &{} \vartheta _{ce} &{} \chi _{ce} &{} \chi _{ce} &{} \pi _{ce}\\ \mu _{ce}^{*} &{} \chi _{ce}^{*} &{} \chi _{ce}^{*} &{} \tau _{ce} &{} \chi _{ce}^{*} &{} \vartheta _{ce} &{} \tau _{ce} &{} \varepsilon _{ce}\\ \mu _{ce}^{*} &{} \chi _{ce}^{*} &{} \chi _{ce}^{*} &{} \tau _{ce} &{} \chi _{ce}^{*} &{} \tau _{ce} &{} \vartheta _{ce} &{} \varepsilon _{ce}\\ \alpha _{ce}e^{-6i\theta } &{} \pi _{ce}^{*} &{} \pi _{ce}^{*} &{} \varepsilon _{ce}^{*} &{} \pi _{ce}^{*} &{} \varepsilon _{ce}^{*} &{} \varepsilon _{ce}^{*} &{} \alpha _{ce} \end{pmatrix} \end{aligned}$$

  (32)

  with

  $$\begin{aligned} \alpha _{ce}= & {} \frac{1}{8}\left[ 2+3p\left\{ 1+\beta _{ce}\cos (2\nu tx_{0})\right\} \right] , \\ \gamma _{ce}= & {} -\frac{p}{8}e^{2i\theta }\left[ 1-\beta _{ce}\left\{ \cos (2\nu tx_{0})-2i\sin (2\nu tx_{0})\right\} \right] , \\ \tau _{ce}= & {} \frac{p}{8}\left[ 1-\beta _{ce}\cos (2\nu tx_{0})\right] ,\quad \mu _{ce}=\gamma _{ce}e^{2i\theta },\quad \varepsilon _{ce}=\pi _{ce}e^{-2i\theta }, \\ \pi _{ce}= & {} \frac{p}{8}e^{4i\theta }\left[ -1+\beta _{ce}\left\{ \cos (2\nu tx_{0})+2i\sin (2\nu tx_{0})\right\} \right] ,\quad \chi _{ce}=\tau _{ce}e^{2i\theta }, \\ \vartheta _{ce}= & {} \frac{1}{8}\left[ 2-p\left\{ 1+\beta _{ce}\cos (2\nu tx_{0})\right\} \right] \quad \text {and} \quad \beta _{ce}=\frac{\sin (\nu tx_{m})}{\nu tx_{m}}. \end{aligned}$$

• Bipartite environments coupling: Here, $x_A = x_B \ne x_C$, and the density matrix $\rho _{be}$ is derived from:

  $$\begin{aligned} {\rho _{be}}\left( t\right) =\int _{d^{-}}^{d^{+}} {\int _{d^{-}}^{d^{+}}}{\hbox {d}{x_{A}}\hbox {d}{x_{C}} P\left( {x_{A}}\right) P\left( {x_{C}}\right) \rho \left( {{x_{A}},{x_{C}},t}\right) } \end{aligned}$$

  (33)

  where $\rho \left( {{x_{A}},{x_{C}},t}\right) ={\mathcal {U}}\left( {{x_{A}},{x_{C}},t}\right) \rho (0)\mathcal {U}^{\dag }\left( {{x_{A}},{x_{C}},t}\right) .$ It finally reads:

  $$\begin{aligned} \rho _{be}(t)=\frac{1}{2}\begin{pmatrix}\alpha _{be} &{} \,\,\gamma _{be}\,\, &{} \,\,\mu _{be}\,\, &{} \,\,\lambda _{be}\,\, &{} \,\,\mu _{be}\,\, &{} \,\,\lambda _{be}\,\, &{} \,\,\pi _{be}\,\, &{} \,\tau _{be}\\ \gamma _{be}^{*} &{} \vartheta _{be} &{} \kappa _{be} &{} \xi _{be} &{} \kappa _{be} &{} \xi _{be} &{} \chi _{be} &{} \varLambda _{be}\\ \mu _{be}^{*} &{} \kappa _{be}^{*} &{} \varpi _{be} &{} \varXi _{de} &{} \eta _{be} &{} \varXi _{de} &{} \varDelta _{be} &{} \varepsilon _{be}\\ \lambda _{be}^{*} &{} \xi _{be}^{*} &{} \varXi _{de}^{*} &{} \varpi _{be} &{} \varXi _{de}^{*} &{} \eta _{be} &{} \kappa _{be}^{*} &{} T\\ \mu _{be}^{*} &{} \kappa _{be}^{*} &{} \eta _{be} &{} \varXi _{de} &{} \varpi _{be} &{} \varXi _{de} &{} \varDelta _{be} &{} \varepsilon _{be}\\ \lambda _{be}^{*} &{} \xi _{be}^{*} &{} \varXi _{de}^{*} &{} \eta _{be} &{} \varXi _{de}^{*} &{} \varpi _{be} &{} \kappa _{be}^{*} &{} T\\ \pi _{be}^{*} &{} \chi _{be}^{*} &{} \varDelta _{be}^{*} &{} \kappa _{be} &{} \varDelta _{be}^{*} &{} \kappa _{be} &{} \vartheta _{be} &{} \nu _{de}\\ \tau _{be}^{*} &{} \varLambda _{be}^{*} &{} \varepsilon _{be}^{*} &{} T^{*} &{} \varepsilon _{be}^{*} &{} T^{*} &{} \nu _{de}^{*} &{} \alpha _{be} \end{pmatrix}, \end{aligned}$$

  (34)

  where

  $$\begin{aligned} \alpha _{be}= & {} \frac{1}{8}\left[ 2+p\left\{ 1+\beta _{ce}\cos (2\nu tx_{0})+4\beta _{de}\cos ^{2}(\nu tx_{0})\right\} \right] , \\ \gamma _{be}= & {} \frac{p}{8}e^{2i\theta }\left[ -1+\beta _{ce}\cos (2\nu tx_{0})-2i\beta _{de}\sin (2\nu tx_{0})\right] ,\quad \pi _{be}=\gamma _{be}e^{2i\theta }, \\ \tau _{be}= & {} \frac{p}{8}e^{6i\theta }\left[ 3+\beta _{ce}\cos (2\nu tx_{0})+4\beta _{de}\cos ^{2}(\nu tx_{0})\right] ,\quad \varLambda _{be}=\gamma _{be}^{*}e^{6i\theta }, \\ \chi _{be}= & {} \frac{p}{8}e^{2i\theta }\left[ 3+\beta _{ce}\cos (2\nu tx_{0})-4\beta _{de}\cos ^{2}(\nu tx_{0})\right] ,\quad \nu _{de}=\varLambda _{be}e^{-2i\theta }, \\ \vartheta _{be}= & {} \frac{1}{8}\left[ 2+p\left\{ 1+\beta _{ce}\cos (2\nu tx_{0})-4\beta _{de}\cos ^{2}(\nu tx_{0})\right\} \right] , \\ \kappa _{be}= & {} \frac{ip}{8}\left[ -\beta _{ce}\sin (2\nu tx_{0})+2\beta _{de}\sin (\nu tx_{0})e^{-i\nu tx_{0}}\right] ,\quad \xi _{be}=\kappa _{be}e^{2i\theta }, \\ \mu _{be}= & {} -\frac{ip}{8}e^{2i\theta }\left[ \beta _{ce}\sin (2\nu tx_{0})+2\beta _{de}\sin (\nu tx_{0})e^{-i\nu tx_{0}}\right] ,\quad \varDelta _{be}=\kappa _{be}^{*}e^{2i\theta } \\ \varpi _{be}= & {} \frac{1}{8}\left[ 2-p\left\{ 1+\beta _{ce}\cos (2\nu tx_{0})\right\} \right] ,\quad \lambda _{be}=\mu _{be}e^{2i\theta }, \\ \eta _{be}= & {} \frac{p}{8}\left[ 1-\beta _{ce}\cos (2\nu tx_{0})\right] ,\quad \varXi _{de}=\eta _{be}e^{2i\theta }, \\ \varepsilon _{be}= & {} \frac{ip}{8}e^{4i\theta }\left[ \beta _{ce}\sin (2\nu tx_{0})+2\beta _{de}\sin (\nu tx_{0})e^{i\nu tx_{0}}\right] . \end{aligned}$$