Skip to main content

Advertisement

Springer Nature Link
Log in

Generalized quantum no-go theorems of pure states

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

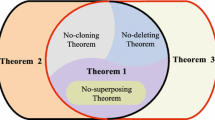
Various results of the no-cloning theorem, no-deleting theorem and no-superposing theorem in quantum mechanics have been proved using the superposition principle and the linearity of quantum operations. In this paper, we investigate general transformations forbidden by quantum mechanics in order to unify these theorems. First, we prove that any useful information cannot be created from an unknown pure state which is randomly chosen from a Hilbert space according to the Harr measure. And then, we propose a unified no-go theorem based on a generalized no-superposing result. The new theorem includes the no-cloning theorem, no-anticloning theorem, no-partial-erasure theorem, no-splitting theorem, no-superposing theorem or no-encoding theorem as a special case. Moreover, it implies various new results. Third, we extend the new theorem into another form that includes the no-deleting theorem as a special case.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Wootters, W.K., Zurek, W.H.: A single quantum cannot be cloned. Nature 299, 802 (1982)

    Article  ADS  MATH  Google Scholar 

  2. Diecks, D.: Communication by EPR devices. Phys. Lett. A 92, 271 (1982)

    Article  ADS  Google Scholar 

  3. Yuen, H.P.: Amplification of quantum states and noiseless photon amplifiers. Phys. Lett. A 113, 405–407 (1986)

    Article  ADS  MathSciNet  Google Scholar 

  4. Peres, A.: Quantum Theory: Concepts and Methods. Kluwer Academic Publishers, Norwell (1995)

    MATH  Google Scholar 

  5. Barnum, H., Caves, C.M., Fuchs, C.A., Jozsa, R., Schumacher, B.: Noncommuting mixed states cannot be broadcast. Phys. Rev. Lett. 76, 2818 (1996)

    Article  ADS  Google Scholar 

  6. Barnum, H., Barrett, J., Leifer, M., Wilce, A.: Generalized no-broadcasting theorem. Phys. Rev. Lett. 99, 240501 (2007)

    Article  ADS  Google Scholar 

  7. Kalev, A., Hen, I.: No-broadcasting theorem and its classical counterpart. Phys. Rev. Lett. 100, 210502 (2008)

    Article  ADS  Google Scholar 

  8. Piani, M., Horodecki, P., Horodecki, R.: No-local-broadcasting theorem for multipartite quantum correlations. Phys. Rev. Lett. 100, 090502 (2008)

    Article  ADS  Google Scholar 

  9. Luo, S.L.: On quantum no-broadcasting. Lett. Math. Phys. 92, 143 (2010)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. Luo, S.L., Sun, W.: Decomposition of bipartite states with applications to quantum no-broadcasting theorems. Phys. Rev. A 82, 012338 (2010)

    Article  ADS  Google Scholar 

  11. Einstein, A., Podolsky, B., Rosen, N.: Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777 (1935)

    Article  ADS  MATH  Google Scholar 

  12. Bell, J.S.: On the Einstein Podolsky Rosen paradox. Physics 1, 195 (1964)

    Article  MathSciNet  Google Scholar 

  13. Greenberger, D.M., Horne, M.A., Zeilinger, A.: Bell’s theorem without inequalities. In: Kafatos, M. (ed.) Bell’s Theorem, Quantum Theory and Conceptions of the Universe, pp. 69–72. Springer, Dordrecht (1989)

    Google Scholar 

  14. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. Gisin, N.: Bell’s inequality holds for all non-product states. Phys. Lett. A 154, 201 (1991)

    Article  ADS  MathSciNet  Google Scholar 

  16. Branciard, C., Rosset, D., Gisin, N., Pironio, S.: Bilocal versus nonbilocal correlations in entanglement-swapping experiments. Phys. Rev. A 85, 032119 (2012)

    Article  ADS  Google Scholar 

  17. Chaves, R.: Polynomial bell inequalities. Phys. Rev. Lett. 116, 010402 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. Luo, M.: Computationally efficient nonlinear Bell inequalities for general quantum networks. Phys. Rev. Lett. 120, 140402 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  19. Lindblad, G.: A general no-cloning theorem. Lett. Math. Phys. 47, 189 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  20. Barnum, H., Barrett, J., Leifer, M., Wilce, A.: Cloning and broadcasting in generic probabilistic theories. arXiv:quant-ph/0611295 (2006)

  21. Barnum, H., Barrett, J., Leifer, M., Wilce, A.: Generalized no-broadcasting theorem. Phys. Rev. Lett. 99, 240501 (2007)

    Article  ADS  Google Scholar 

  22. Kaniowski, K., Lubnauer, K., Łuczak, A.: Multicloning and multibroadcasting in operator algebras. Q. J. Math. 66, 191–192 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  23. Stinespring, W.F.: Positive functions on \(C^*\)-algebras. Proc. Am. Math. Soc. 6, 211–216 (1955)

    MathSciNet  MATH  Google Scholar 

  24. Choi, M.-D.: Completely positive maps on complex matrices. Linear Algebra Appl. 10, 285–290 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  25. Kraus, K.: States, Effects and Operations: Fundamental Notions of Quantum Theory. Springer, Berlin (1983)

    Book  MATH  Google Scholar 

  26. Miyadera, T., Imai, H.: No-cloning theorem on quantum logics. J. Math. Phys. 50, 1063 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  27. Niestegge, G.: Non-classical conditional probability and the quantum no-cloning theorem. Phys. Scr. 90, 095101 (2015)

    Article  ADS  Google Scholar 

  28. D’Ariano, G.M., Perinotti, P.: Quantum no-stretching: a geometrical interpretation of the no-cloning theorem. Phys. Lett. A 373, 2416–2419 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  29. Abramsky, S.: No-cloning in categorical quantum mechanics. In: Gay, S., Mackie, I. (eds.) Semantic Techniques in Quantum Computation, pp. 1–28. Cambridge University Press, Cambridge (2010)

    Google Scholar 

  30. Bennett, C.H., Brassard, G.: In: Proceedings IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, p. 175. IEEE, New York (1984)

  31. Shor, P.W., Preskill, J.: Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441 (2000)

    Article  ADS  Google Scholar 

  32. Lo, H.-K., Chau, H.F.: Unconditional security of quantum key distribution over arbitrarily long distances. Science 283, 2050–2056 (1999)

    Article  ADS  Google Scholar 

  33. Cerf, N.J., Bourennane, M., Karlsson, A., Gisin, N.: Security of quantum key distribution using \(d\)-level systems. Phys. Rev. Lett. 88(12), 127902 (2002)

    Article  ADS  Google Scholar 

  34. Scarani, V., Bechmann-Pasquinucci, H., Cerf, N.J., Dužek, M., Lütkenhaus, N., Peev, M.: The security of practical quantum key distribution. Rev. Mod. Phys. 81(3), 1301 (2009)

    Article  ADS  Google Scholar 

  35. Gisin, N., Ribordy, G., Tittel, W., Zbinden, H.: Towards practical and fast quantum cryptography. Rev. Mod. Phys. 74, 145 (2002)

    Article  ADS  MATH  Google Scholar 

  36. Pati, A.K., Braunstein, S.L.: Impossibility of deleting an unknown quantum state. Nature 404, 104 (2000)

    Google Scholar 

  37. Oszmaniec, M., Grudka, A., Horodecki, M., Wójcik, A.: Creation of superposition of unknown quantum states. Phys. Rev. Lett. 116, 110403 (2016)

    Article  ADS  Google Scholar 

  38. Alvarez-Rodriguez, U., Sanz, M., Lamata, L., Solano, E.: The forbidden quantum adder. Sci. Rep. 5, 11983 (2015)

    Article  ADS  Google Scholar 

  39. Luo, M.L., Li, H.R., Lai, H., Wang, X.: Unified quantum no-go theorems and transforming of quantum pure states in a restricted set. Quantum Inf. Process. 16, 297 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  40. Amico, L., Fazio, R., Osterloh, A., Vedral, V.: Entanglement in many-body systems. Rev. Mod. Phys. 80, 517–576 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  41. Pati, A.K.: General impossible operations in quantum information. Phys. Rev. A 66, 062319 (2002)

    Article  ADS  Google Scholar 

  42. Pati, A.K., Sanders, B.C.: No-partial erasure of quantum information. Phys. Lett. A 359, 31–36 (2006)

    Article  ADS  Google Scholar 

  43. Zhou, D.L., Zeng, B., You, L.: Quantum information cannot be split into complementary parts. Phys. Lett. A 352, 41 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  44. Riesz, F.C.: Sur les operations fonctionelles lineaires. R. Acad. Sci. Paris. 149, 974–977 (1909)

    MATH  Google Scholar 

  45. Duan, L.M., Guo, G.C.: A probabilistic cloning machine for replicating two non-orthogonal states. Phys. Lett. A 243, 261 (1998)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  46. Duan, L.M., Guo, G.C.: Probabilistic cloning and identification of linearly independent quantum states. Phys. Rev. Lett. 80, 4999 (1998)

    Article  ADS  Google Scholar 

  47. Chefles, A., Barnett, S.M.: Quantum state separation, unambiguous discrimination and exact cloning. J. Phys. A 31, 10097 (1998)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  48. Chefles, A.: Unambiguous discrimination between linearly independent quantum states. Phys. Lett. A 239, 339–347 (1998)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  49. Chefles, A., Jozsa, R., Winter, A.: On the existence of physical transformations between sets of quantum states. Int. J. Quantum Inf. 02, 11–21 (2004)

    Article  MATH  Google Scholar 

  50. Braunstein, S.L., Pati, A.K.: Quantum information cannot be completely hidden in correlations: implications for the black-hole information paradox. Phys. Rev. Lett. 98, 080502 (2007)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  51. Bennett, C.H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  52. Hillery, M., Bužek, V., Berthiaume, A.: Quantum secret sharing. Phys. Rev. A 59, 1829 (1999)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  53. Cleve, R., Gottesman, D., Lo, H.-K.: How to share a quantum secret? Phys. Rev. Lett. 83, 648 (1999)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank Luming Duan and Yaoyun Shi. This work was supported by the National Natural Science Foundation of China (Nos. 61772437, 61702427), Sichuan Youth Science and Technique Foundation (No. 2017JQ0048) and Fundamental Research Funds for the Central Universities (No. XDJK2016C043), Chuying Fellowship and the Doctoral Program of Higher Education (No. SWU115091).

Author information

Authors and Affiliations

  1. Information Security and National Computing Grid Laboratory, Southwest Jiaotong University, Chengdu, 610031, China

    Hui-Ran Li & Ming-Xing Luo

  2. School of Computer and Information Science, Southwest University, Chongqing, 400715, China

    Hong Lai

Authors
  1. Hui-Ran Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ming-Xing Luo
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Hong Lai
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ming-Xing Luo.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, HR., Luo, MX. & Lai, H. Generalized quantum no-go theorems of pure states. Quantum Inf Process 17, 168 (2018). https://doi.org/10.1007/s11128-018-1936-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-018-1936-4

Keywords