Free and bound entanglement dynamics in qutrit systems under Markov and non-Markov classical noise

Abstract

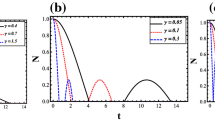
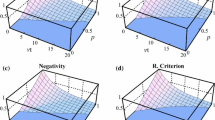
We investigate in detail the dynamics of decoherence, free and bound entanglements, and the conversion from one to another (quantum state transitions), in a two non-interacting qutrits system initially entangled and subject to independents or a common classical noise. Both Markovian and non-Markovian environments are considered. Furthermore, isotropic and bound entangled states for qutrits systems are considered as initial states. We show the efficiency of the formers over the latters against decoherence, and in preserving quantum entanglement. The loss of coherence increases monotonically with time up to a saturation value depending upon the initial state parameter and is stronger in a collective Markov environment. For the non-Markov regime the presence or absence of entanglement revival and entanglement sudden death phenomena is deduced depending on both the peculiar characteristics of the noise, the physical setup and the initial state of the system. We demonstrate distillability sudden death for conveniently selected parameters in bound entangled states; meanwhile, it is completely absent for isotropic states, where entanglement sudden death is avoided for dynamic noise independently of the noise regime and the physical setup. Our results indicate that distillability sudden death under the Markov/non-Markov noise considered can be avoided depending upon the physical setup.

Appendix: Explicit forms of the time-evolved states

We present the explicit forms of the various time-evolved states under the effects of the classical noise models considered, initially entangled in either state of Eqs. (5) and (6), and for both physical setups considered.

1.1 Static noise

1.1.1 Isotropic states

When the subsystems are initially entangled in isotropic states and subject to static noise, their density matrices from Eqs. (10) and (11) take the following form:

$$\begin{aligned}&\rho _{\text {de(ce)}}(p,t)\nonumber \\&\quad =\frac{1}{72}\left( \begin{array}{ccccccccc} \rho _{11}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{13}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{15}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{13}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{19}^{\text {de(ce)}}\\ -\rho _{12}^{\text {de(ce)}} &{} \rho _{22}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{25}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} -\rho _{12}^{\text {de(ce)}}\\ \rho _{13}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{33}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{35}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{37}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{13}^{\text {de(ce)}}\\ -\rho _{12}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{22}^{\text {de(ce)}} &{} \rho _{25}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} -\rho _{12}^{\text {de(ce)}}\\ \rho _{15}^{\text {de(ce)}} &{} -\rho _{25}^{\text {de(ce)}} &{} \rho _{35}^{\text {de(ce)}} &{} -\rho _{25}^{\text {de(ce)}} &{} \rho _{55}^{\text {de(ce)}} &{} -\rho _{25}^{\text {de(ce)}} &{} \rho _{35}^{\text {de(ce)}} &{} -\rho _{25}^{\text {de(ce)}} &{} \rho _{15}^{\text {de(ce)}}\\ -\rho _{12}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{25}^{\text {de(ce)}} &{} \rho _{22}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} -\rho _{12}^{\text {de(ce)}}\\ \rho _{13}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{37}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{35}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{33}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{13}^{\text {de(ce)}}\\ -\rho _{12}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{25}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{22}^{\text {de(ce)}} &{} -\rho _{12}^{\text {de(ce)}}\\ \rho _{19}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{13}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{15}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{13}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{11}^{\text {de(ce)}} \end{array}\right) \nonumber \\ \end{aligned}$$

(15)

where

$$\begin{aligned} \rho _{11}^{\text {de(ce)}}= & {} \text {X}^{+};\quad \rho _{33}^{\text {de(ce)}}=\text {X}^{-}\quad \text {with}\quad \text {X}^{\pm }=8+p\left( 1\pm 12\alpha _{\text {de(ce)}}+3\xi _{\text {de(ce)}}\right) \\ \rho _{12}^{\text {de(ce)}}= & {} -\text {Y}^{+};\quad \rho _{23}^{\text {de(ce)}}=\text {Y}^{-}\quad \text {with}\quad \text {Y}^{\pm }=6ip\sqrt{2}\left( \Omega _{\text {de(ce)}}C_{2}(t)\pm \Pi _{\text {de(ce)}}\right) S_{2}(t)\\ \rho _{13}^{\text {de(ce)}}= & {} -\rho _{24}^{\text {de(ce)}}=3p\left( -1+\xi _{\text {de(ce)}}\right) ;\quad \rho _{22}^{\text {de(ce)}}=2\left( 4-p(1+3\xi _{\text {de(ce)}})\right) \\ \rho _{15}^{\text {de(ce)}}= & {} \text {B}^{+};\quad \rho _{35}^{\text {de(ce)}}=\text {B}^{-}\quad \text {with}\quad \text {B}^{\pm }=6p\left( 1\pm 2\alpha _{\text {de(ce)}}+\xi _{\text {de(ce)}}\right) \\ \rho _{19}^{\text {de(ce)}}= & {} \text {Z}^{+};\quad \rho _{37}^{\text {de(ce)}}=\text {Z}^{-}\quad \text {with}\quad \text {Z}^{\pm }=3p\left( 3\pm 4\alpha _{\text {de(ce)}}+\xi _{\text {de(ce)}}\right) \\ \rho _{25}^{\text {de(ce)}}= & {} 6ip\sqrt{2}\Omega _{\text {de(ce)}}S_{4}(t);\quad \rho _{55}^{\text {de(ce)}}=4\left( 2+p(1+3\xi _{\text {de(ce)}})\right) \end{aligned}$$

where

$$\begin{aligned} \alpha _{\text {de(ce)}}= & {} \Pi _{\text {de(ce)}}C_{2}(t);\quad \xi _{\text {de(ce)}}=\Omega _{\text {de(ce)}}C_{4}(t);\quad \Pi _{\text {de}}=K_{(1)}^{2};\quad \Pi _{\text {ce}}=K_{(2)};\\ \Omega _{\text {de}}= & {} K_{(2)}^{2};\quad \Omega _{\text {ce}}=K_{(4)}\\ \Pi _{\text {de}}= & {} K_{(1)}^{2};\quad \Pi _{\text {ce}}=K_{(2)};\quad \Omega _{\text {de}}=K_{(2)}^{2};\quad \Omega _{\text {ce}}=K_{(4)}\\ C_{n}(t)= & {} \cos (ngt\vartheta _{0});\quad S_{n}(t)=\sin (ngt\vartheta _{0});\\&K_{(n)}=\frac{2\sin (ngt\vartheta _{m}/2)}{ngt\vartheta _{m}},\quad n\in \left\{ 1,2,4\right\} \end{aligned}$$

1.1.2 Bound entangled states

When the subsystems are initially prepared in bound entangled states and then subject to a static noise, Eqs. (10) and (11) give:

$$\begin{aligned}&\rho _{\text {de(ce)}}(\alpha ,t)\nonumber \\&\quad =\frac{1}{2688}\left( \begin{array}{ccccccccc} s_{11}^{\text {de(ce)}} &{} s_{12}^{\text {de(ce)}} &{} s_{13}^{\text {de(ce)}} &{} s_{14}^{\text {de(ce)}} &{} s_{15}^{\text {de(ce)}} &{} s_{16}^{\text {de(ce)}} &{} s_{17}^{\text {de(ce)}} &{} s_{18}^{\text {de(ce)}} &{} s_{19}^{\text {de(ce)}}\\ -s_{12}^{\text {de(ce)}} &{} s_{22}^{\text {de(ce)}} &{} s_{23}^{\text {de(ce)}} &{} s_{24}^{\text {de(ce)}} &{} s_{25}^{\text {de(ce)}} &{} s_{26}^{\text {de(ce)}} &{} s_{27}^{\text {de(ce)}} &{} s_{28}^{\text {de(ce)}} &{} -s_{16}^{\text {de(ce)}}\\ s_{13}^{\text {de(ce)}} &{} -s_{23}^{\text {de(ce)}} &{} s_{33}^{\text {de(ce)}} &{} s_{34}^{\text {de(ce)}} &{} s_{35}^{\text {de(ce)}} &{} -s_{23}^{\text {de(ce)}} &{} s_{37}^{\text {de(ce)}} &{} s_{34}^{\text {de(ce)}} &{} s_{13}^{\text {de(ce)}}\\ -s_{14}^{\text {de(ce)}} &{} s_{24}^{\text {de(ce)}} &{} -s_{34}^{\text {de(ce)}} &{} s_{44}^{\text {de(ce)}} &{} s_{45}^{\text {de(ce)}} &{} s_{28}^{\text {de(ce)}} &{} s_{47}^{\text {de(ce)}} &{} s_{48}^{\text {de(ce)}} &{} -s_{18}^{\text {de(ce)}}\\ s_{15}^{\text {de(ce)}} &{} -s_{25}^{\text {de(ce)}} &{} s_{35}^{\text {de(ce)}} &{} -s_{45}^{\text {de(ce)}} &{} s_{55}^{\text {de(ce)}} &{} -s_{25}^{\text {de(ce)}} &{} s_{57}^{\text {de(ce)}} &{} -s_{45}^{\text {de(ce)}} &{} s_{15}^{\text {de(ce)}}\\ -s_{16}^{\text {de(ce)}} &{} s_{26}^{\text {de(ce)}} &{} s_{23}^{\text {de(ce)}} &{} s_{28}^{\text {de(ce)}} &{} s_{25}^{\text {de(ce)}} &{} s_{22}^{\text {de(ce)}} &{} s_{27}^{\text {de(ce)}} &{} s_{24}^{\text {de(ce)}} &{} -s_{12}^{\text {de(ce)}}\\ s_{17}^{\text {de(ce)}} &{} -s_{27}^{\text {de(ce)}} &{} s_{37}^{\text {de(ce)}} &{} -s_{47}^{\text {de(ce)}} &{} s_{57}^{\text {de(ce)}} &{} -s_{27}^{\text {de(ce)}} &{} s_{77}^{\text {de(ce)}} &{} -s_{47}^{\text {de(ce)}} &{} s_{17}^{\text {de(ce)}}\\ -s_{18}^{\text {de(ce)}} &{} s_{28}^{\text {de(ce)}} &{} -s_{34}^{\text {de(ce)}} &{} s_{48}^{\text {de(ce)}} &{} s_{45}^{\text {de(ce)}} &{} s_{24}^{\text {de(ce)}} &{} s_{47}^{\text {de(ce)}} &{} s_{44}^{\text {de(ce)}} &{} -s_{14}^{\text {de(ce)}}\\ s_{19}^{\text {de(ce)}} &{} s_{16}^{\text {de(ce)}} &{} s_{13}^{\text {de(ce)}} &{} s_{18}^{\text {de(ce)}} &{} s_{15}^{\text {de(ce)}} &{} s_{12}^{\text {de(ce)}} &{} s_{17}^{\text {de(ce)}} &{} s_{14}^{\text {de(ce)}} &{} s_{11}^{\text {de(ce)}} \end{array}\right) \nonumber \\ \end{aligned}$$

(16)

with

$$\begin{aligned} s_{11}^{\text {de}}= & {} 306-80\Pi _{\text {de}}+C_{2}(t)\left( -20\Pi _{\text {ce}}+48\Pi _{\text {de}}\right) +\left( -15+17C_{4}(t)\right) \Omega _{\text {de}}\\ s_{15}^{\text {de}}= & {} 64+8\Pi _{\text {de}}\left( 5+11C_{2}(t)\right) +2\Omega _{\text {de}}\left( 15+17C_{4}(t)\right) \\ s_{24}^{\text {de}}= & {} 64+40\Pi _{\text {de}}\left( -1+C_{2}(t)\right) -2\Omega _{\text {de}}\left( 15+17C_{4}(t)\right) \\ s_{25}^{\text {de}}= & {} -8i\sqrt{2}S_{1}\left( \Pi _{\text {ce}}C_{1}(t)\left( 5-17\Pi _{\text {ce}}C_{2}(t)\right) -(1+3C_{2}(t)\Pi _{\text {ce}})y_{1}(\alpha )\right) \\ s_{28}^{\text {de}}= & {} 44-40\Pi _{\text {ce}}C_{2}(t)+2\Omega _{\text {de}}\left( 15-17C_{4}(t)\right) \\ s_{45}^{\text {de}}= & {} 4i\sqrt{2}S_{1}(t)\left( -10\Pi _{\text {ce}}C_{1}(t)+17\Omega _{\text {de}}\left( C_{1}(t)+C_{3}(t)\right) -2(1+3\Pi _{\text {ce}}C_{2}(t))y_{1}(\alpha )\right) \\ s_{55}^{\text {de}}= & {} 328-80\Pi _{\text {ce}}C_{2}(t)+4\Omega _{\text {de}}\left( -15+17C_{4}(t)\right) \\ s_{12}^{\text {de}}= & {} \text {A}_{\text {de}}^{+};\quad s_{14}^{\text {de}}=\text {A}_{\text {de}}^{-};\quad s_{16}^{\text {de}}=\text {B}_{\text {de}}^{+};\quad s_{34}^{\text {de}}=\text {B}_{\text {de}}^{-};\quad s_{18}^{\text {de}}=\text {D}_{\text {de}}^{+};\quad s_{27}^{\text {de}}=-\text {D}_{\text {de}}^{-};\\ s_{35}^{\text {de}}= & {} \text {E}_{\text {de}}^{-}\\ s_{57}^{\text {de}}= & {} \text {E}_{\text {de}}^{+};\quad s_{19}^{\text {de}}=\text {F}_{\text {de}}^{+};\quad s_{37}^{\text {de}}=\text {F}_{\text {de}}^{-};\quad s_{33}^{\text {de}}=\text {G}_{\text {de}}^{+};\quad s_{77}^{\text {de}}=\text {G}_{\text {de}}^{-};\quad s_{26}^{\text {de}}=\text {H}_{\text {de}}^{+};\\ s_{48}^{\text {de}}= & {} \text {H}_{\text {de}}^{-}\\ s_{13}^{\text {de}}= & {} \text {I}_{\text {de}}^{+};\quad s_{17}^{\text {de}}=\text {I}_{\text {de}}^{-};\quad s_{22}^{\text {de}}=\text {J}_{\text {de}}^{-};\quad s_{44}^{\text {de}}=\text {J}_{\text {de}}^{+};\quad s_{23}^{\text {de}}=\text {L}_{\text {de}}^{+};\quad s_{47}^{\text {de}}=\text {L}_{\text {de}}^{-} \end{aligned}$$

with

$$\begin{aligned} \text {A}_{\text {de}}^{\pm }= & {} i\sqrt{2}\left( -17S_{4}(t)\Omega _{\text {de}}+2S_{2}(t)\left( 5\Pi _{\text {ce}}-12\Pi _{\text {de}}\right) \right. \\&\left. \pm \,2\left( -2S_{1}(t)+3\left( 3S_{1}(t)+S_{3}(t)\right) \Pi _{\text {ce}}\right) y_{1}(\alpha )\right) \\ \text {B}_{\text {de}}^{\pm }= & {} -i\sqrt{2}\left( 17S_{4}(t)\Omega _{\text {de}}+S_{2}(t)\left( 30\Pi _{\text {ce}}\pm 64\Pi _{\text {de}}\right) \right. \\&\left. -\,6\left( -S_{3}\Pi _{\text {ce}}+S_{1}(2+\Pi _{\text {ce}})\right) y_{1}(\alpha )\right) \\ \text {D}_{\text {de}}^{\pm }= & {} -2i\sqrt{2}S_{1}(t)\left( C_{1}(t)\left( \Pi _{\text {ce}}(30+17\Pi _{\text {ce}})\pm 64\Pi _{\text {de}}\right) +17C_{3}(t)\Omega _{\text {de}}\right. \\&\left. -\,6\left( -1+C_{2}\Pi _{\text {ce}}\right) y_{1}(\alpha )\right) \\ \text {E}_{\text {de}}^{\pm }= & {} 64-8\left( 5+11C_{2}\right) \Pi _{\text {de}}+\left( 30+34C_{4}\right) \Omega _{\text {de}}\pm 24\left( C_{1}-C_{3}\right) \Pi _{\text {ce}}y_{1}(\alpha )\\ \text {F}_{\text {de}}^{\pm }= & {} 66+4C_{2}(t)\left( 15\Pi _{\text {ce}}\pm 32\Pi _{\text {de}}\right) +\left( -15+17C_{4}(t)\right) \Omega _{\text {de}}\\ \text {G}_{\text {de}}^{\pm }= & {} 306+80\Pi _{\text {de}}-4C_{2}\left( 5\Pi _{\text {ce}}+12\Pi _{\text {de}}\right) +\left( -15+17C_{4}\right) \Omega _{\text {de}}\\&\pm \,8\left( 2C_{1}+3(C_{1}+C_{3})\Pi _{\text {ce}}\right) y_{1}(\alpha )\\ \text {H}_{\text {de}}^{\pm }= & {} 64-40\left( -1+C_{2}(t)\right) \Pi _{\text {de}}-2\left( 15+17C_{4}(t)\right) \Omega _{\text {de}}\\&\pm \,24\left( C_{1}(t)-C_{3}(t)\right) \Pi _{\text {ce}}y_{1}(\alpha )\\ \text {I}_{\text {de}}^{\pm }= & {} -22+20\Pi _{\text {ce}}C_{2}(t)-\Omega _{\text {de}}\left( 15-17C_{4}(t)\right) \\&\pm \,12\left( -2C_{1}(t)+\left( C_{1}(t)+C_{3}(t)\right) \Pi _{\text {ce}}\right) y_{1}(\alpha )\\ \text {J}_{\text {de}}^{\pm }= & {} 2\left( 142+20\Pi _{\text {ce}}C_{2}(t)-17\Omega _{\text {de}}C_{4}(t)+15\Omega _{\text {de}}\right. \\&\left. \pm \,4\left( 2C_{1}(t)+3\Pi _{\text {ce}}\left( C_{1}(t)+C_{3}(t)\right) \right) y_{1}(\alpha )\right) \\ \text {L}_{\text {de}}^{\pm }= & {} i\sqrt{2}\left( 17S_{4}(t)\Omega _{\text {de}}-2S_{2}(t)(5\Pi _{\text {ce}}+12\Pi _{\text {de}})\right. \\&\left. \pm \,2\left( 2S_{1}(t)+3\left( S_{1}(t)+3S_{3}(t)\right) \Pi _{\text {ce}}\right) y_{1}(\alpha )\right) \end{aligned}$$

where

$$\begin{aligned} y_{1}(\alpha )= & {} K_{(1)}(5-2\alpha )\\ y_{3}(\alpha )= & {} K_{(3)}(5-2\alpha ) \end{aligned}$$

and

$$\begin{aligned} s_{11}^{\text {ce}}= & {} 211+28\Pi _{\text {ce}}C_{2}(t)+17\Omega _{\text {ce}}C_{4}(t);\quad s_{15}^{\text {ce}}=2\left( 67+44\Pi _{\text {ce}}C_{2}(t)+17\Omega _{\text {ce}}C_{4}(t)\right) \\ s_{19}^{\text {ce}}= & {} 51+188\Pi _{\text {ce}}C_{2}(t)+17\Omega _{\text {ce}}C_{4}(t);\quad s_{24}^{\text {ce}}=-3+20\Pi _{\text {ce}}C_{2}(t)-17\Omega _{\text {ce}}C_{4}(t)\\ s_{28}^{\text {ce}}= & {} 2\left( 37-20\Pi _{\text {ce}}C_{2}(t)-17\Omega _{\text {ce}}C_{4}(t)\right) ;\quad s_{37}^{\text {ce}}=17\left( 3-4\Pi _{\text {ce}}C_{2}(t)+\Omega _{\text {ce}}C_{4}(t)\right) \\ s_{55}^{\text {ce}}= & {} 4\left( 67-20\Pi _{\text {ce}}C_{2}(t)+17\Omega _{\text {ce}}C_{4}(t)\right) ;\quad s_{12}^{\text {ce}}=\text {A}_{ce}^{+};\quad s_{14}^{\text {ce}}=\text {A}_{\text {ce}}^{-}\\ s_{16}^{\text {ce}}= & {} \text {B}_{\text {ce}}^{-};\quad s_{18}^{\text {ce}}=\text {B}_{\text {ce}}^{+};\quad s_{13}^{\text {ce}}=\text {D}_{\text {ce}}^{-};\quad s_{17}^{\text {ce}}=\text {D}_{\text {ce}}^{+};\quad s_{27}^{\text {ce}}=\text {E}_{\text {ce}}^{-};\quad s_{34}^{\text {ce}}=-\text {E}_{\text {ce}}^{+};\\ s_{22}^{\text {ce}}= & {} \text {F}_{\text {ce}}^{-};\quad s_{44}^{\text {ce}}=\text {F}_{\text {ce}}^{+};\quad s_{33}^{\text {ce}}=\text {G}_{\text {ce}}^{+};\quad s_{77}^{\text {ce}}=\text {G}_{\text {ce}}^{-};\quad s_{23}^{\text {ce}}=\text {H}_{\text {ce}}^{-};\quad s_{47}^{\text {ce}}=\text {H}_{\text {ce}}^{+};\\ s_{26}^{\text {ce}}= & {} \text {I}_{\text {ce}}^{+};\quad s_{48}^{\text {ce}}=\text {I}_{\text {ce}}^{-};\quad s_{35}^{\text {ce}}=\text {J}_{\text {ce}}^{-};\quad s_{57}^{\text {ce}}=\text {J}_{\text {ce}}^{+};\quad s_{35}^{\text {ce}}=\text {L}_{\text {ce}}^{-};\quad s_{57}^{\text {ce}}=\text {L}_{\text {ce}}^{+} \end{aligned}$$

with

$$\begin{aligned} \text {A}_{\text {ce}}^{\pm }= & {} -i\sqrt{2}\left( 14\Pi _{\text {ce}}S_{2}(t)+17\Omega _{\text {ce}}S_{4}(t)\pm 2\left( 7y_{1}(\alpha )S_{1}(t)+3S_{3}(t)y_{3}(\alpha )\right) \right) \\ \text {B}_{\text {ce}}^{\pm }= & {} -i\sqrt{2}\left( 94\Pi _{\text {ce}}S_{2}(t)+17\Omega _{\text {ce}}S_{4}(t)\pm \left( 18y_{1}(\alpha )S_{1}(t)-6S_{3}(t)y_{3}(\alpha )\right) \right) \\ \text {D}_{\text {ce}}^{\pm }= & {} -37+20\Pi _{\text {ce}}C_{2}(t)+17\Omega _{\text {ce}}S_{4}(t)\pm 12\left( C_{1}(t)y_{1}(\alpha )-C_{3}(t)y_{3}(\alpha )\right) \\ \text {E}_{\text {ce}}^{\pm }= & {} -i\sqrt{2}\left( 34\Pi _{\text {ce}}S_{2}(t)-17\Omega _{\text {ce}}S_{4}(t)\pm 6\left( 3y_{1}(\alpha )S_{1}(t)-S_{3}(t)y_{3}(\alpha )\right) \right) \\ \text {F}_{\text {ce}}^{\pm }= & {} 314+40\Pi _{\text {ce}}C_{2}(t)-34\Omega _{\text {ce}}C_{4}(t)\pm 8\left( 5C_{1}(t)y_{1}(\alpha )+3C_{3}(t)y_{3}(\alpha )\right) \\ \text {G}_{\text {ce}}^{\pm }= & {} 371-68\Pi _{\text {ce}}C_{2}(t)+17\Omega _{\text {ce}}C_{4}(t)\pm 8\left( 5C_{1}(t)y_{1}(\alpha )+3C_{3}(t)y_{3}(\alpha )\right) \\ \text {H}_{\text {ce}}^{\pm }= & {} -i\sqrt{2}\left( 34\Pi _{\text {ce}}S_{2}(t)-17\Omega _{\text {ce}}S_{4}(t)\pm 2\left( 5y_{1}(\alpha )S_{1}(t)+9S_{3}(t)y_{3}(\alpha )\right) \right) \\ \text {I}_{\text {ce}}^{\pm }= & {} 74-40\Pi _{\text {ce}}C_{2}(t)-34\Omega _{\text {ce}}C_{4}(t)\pm 24\left( C_{1}(t)y_{1}(\alpha )-C_{3}(t)y_{3}(\alpha )\right) \\ \text {J}_{\text {ce}}^{\pm }= & {} 54-88\Pi _{\text {ce}}C_{2}(t)+34\Omega _{\text {ce}}C_{4}(t)\pm 24\left( C_{1}(t)y_{1}(\alpha )-C_{3}(t)y_{3}(\alpha )\right) \\ \text {L}_{\text {ce}}^{\pm }= & {} 2i\sqrt{2}\left( -10\Pi _{\text {ce}}S_{2}(t)+17\Omega _{\text {ce}}S_{4}(t)\pm 2\left( y_{1}(\alpha )S_{1}(t)-3S_{3}(t)y_{3}(\alpha )\right) \right) \end{aligned}$$

1.2 Dynamic noise

1.2.1 Isotropic states

For the dynamic noise model, when the system is initially prepared in state of Eq. (5), density matrices from Eq. (12) take the following form:

$$\begin{aligned}&\rho _{\text {de(ce)}}(t)\nonumber \\&\quad =\frac{1}{72}\left( \begin{array}{ccccccccc} A_{\text {de(ce)}}^{+} &{} 0 &{} B_{\text {de(ce)}} &{} 0 &{} C_{\text {de(ce)}}^{+} &{} 0 &{} B_{\text {de(ce)}} &{} 0 &{} D_{\text {de(ce)}}^{+}\\ 0 &{} E_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0\\ B_{\text {de(ce)}} &{} 0 &{} A_{\text {de(ce)}}^{-} &{} 0 &{} C_{\text {de(ce)}}^{-} &{} 0 &{} D_{\text {de(ce)}}^{-} &{} 0 &{} B_{\text {de(ce)}}\\ 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} E_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0\\ C_{\text {de(ce)}}^{+} &{} 0 &{} C_{\text {de(ce)}}^{-} &{} 0 &{} F_{\text {de(ce)}} &{} 0 &{} C_{\text {de(ce)}}^{-} &{} 0 &{} C_{\text {de(ce)}}^{+}\\ 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} E_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0\\ B_{\text {de(ce)}} &{} 0 &{} D_{\text {de(ce)}}^{-} &{} 0 &{} C_{\text {de(ce)}}^{-} &{} 0 &{} A_{\text {de(ce)}}^{-} &{} 0 &{} B_{\text {de(ce)}}\\ 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} E_{\text {de(ce)}} &{} 0\\ D_{\text {de(ce)}}^{+} &{} 0 &{} B_{\text {de(ce)}} &{} 0 &{} C_{\text {de(ce)}}^{+} &{} 0 &{} B_{\text {de(ce)}} &{} 0 &{} A_{\text {de(ce)}}^{+} \end{array}\right) \nonumber \\ \end{aligned}$$

(17)

where

$$\begin{aligned} A_{\text {de(ce)}}^{\pm }= & {} 8+p\left( 1\pm 12\Phi _{\text {de(ce)}}+3\Psi _{\text {de(ce)}}\right) \\ B_{\text {de(ce)}}= & {} 3p\left( \Psi _{\text {de(ce)}}-1\right) \\ C_{\text {de(ce)}}^{\pm }= & {} 6p\left( 1\pm 2\Phi _{\text {de(ce)}}+\Psi _{\text {de(ce)}}\right) \\ D_{\text {de(ce)}}^{\pm }= & {} 3p\left( 3\pm 4\Phi _{\text {de(ce)}}+\Psi _{\text {de(ce)}}\right) \\ E_{\text {de(ce)}}= & {} 2\left( 4-p(1+3\Psi _{\text {de(ce)}})\right) \\ F_{\text {de(ce)}}= & {} 4\left( 2+p\left( 1+3\Psi _{\text {de(ce)}}\right) \right) \\ \Phi _{\text {de}}= & {} \Gamma _{1}^{2}(t);\quad \Psi _{\text {de}}=\Gamma _{2}^{2}(t);\quad \Phi _{\text {ce}}=\Gamma _{2}(t);\quad \Psi _{\text {ce}}=\Gamma _{4}(t). \end{aligned}$$

1.2.2 Bound entangled states

Here Eq. (12) gives:

$$\begin{aligned} \tilde{\rho }_{\text {de}}(t)= & {} \frac{1}{1344}\left( \begin{array}{ccccccccc} A_{1} &{} 0 &{} B_{1}^{-} &{} 0 &{} C_{1} &{} 0 &{} B_{1}^{+} &{} 0 &{} D_{1}^{+}\\ 0 &{} E_{1}^{+} &{} 0 &{} F_{1} &{} 0 &{} F_{1} &{} 0 &{} G_{1} &{} 0\\ B_{1}^{-} &{} 0 &{} H_{1}^{-} &{} 0 &{} J_{1} &{} 0 &{} D_{1}^{-} &{} 0 &{} B_{1}^{-}\\ 0 &{} F_{1} &{} 0 &{} E_{1}^{-} &{} 0 &{} G_{1} &{} 0 &{} F_{1} &{} 0\\ C_{1} &{} 0 &{} J_{1} &{} 0 &{} K_{1} &{} 0 &{} J_{1} &{} 0 &{} C_{1}\\ 0 &{} F_{1} &{} 0 &{} G_{1} &{} 0 &{} E_{1}^{+} &{} 0 &{} F_{1} &{} 0\\ B_{1}^{+} &{} 0 &{} D_{1}^{-} &{} 0 &{} J_{1} &{} 0 &{} H_{1}^{+} &{} 0 &{} B_{1}^{+}\\ 0 &{} G_{1} &{} 0 &{} F_{1} &{} 0 &{} F_{1} &{} 0 &{} E_{1}^{-} &{} 0\\ D_{1}^{+} &{} 0 &{} B_{1}^{-} &{} 0 &{} C_{1} &{} 0 &{} B_{1}^{+} &{} 0 &{} A_{1} \end{array}\right) \end{aligned}$$

(18)

$$\begin{aligned} \tilde{\rho }_{\text {ce}}(t)= & {} \frac{1}{2688}\left( \begin{array}{ccccccccc} A_{2} &{} 0 &{} B_{2}^{+} &{} 0 &{} C_{2} &{} 0 &{} B_{2}^{-} &{} 0 &{} D_{2}\\ 0 &{} E_{2}^{+} &{} 0 &{} F_{2} &{} 0 &{} -B_{2}^{+} &{} 0 &{} H_{2} &{} 0\\ B_{2}^{+} &{} 0 &{} I_{2}^{-} &{} 0 &{} J_{2}^{+} &{} 0 &{} K_{2} &{} 0 &{} B_{2}^{+}\\ 0 &{} F_{2} &{} 0 &{} E_{2}^{-} &{} 0 &{} H_{2} &{} 0 &{} -B_{2}^{-} &{} 0\\ C_{2} &{} 0 &{} J_{2}^{+} &{} 0 &{} L_{2} &{} 0 &{} J_{2}^{-} &{} 0 &{} C_{2}\\ 0 &{} -B_{2}^{+} &{} 0 &{} H_{2} &{} 0 &{} E_{2}^{+} &{} 0 &{} F_{2} &{} 0\\ B_{2}^{-} &{} 0 &{} K_{2} &{} 0 &{} J_{2}^{-} &{} 0 &{} I_{2}^{+} &{} 0 &{} B_{2}^{-}\\ 0 &{} H_{2} &{} 0 &{} -B_{2}^{-} &{} 0 &{} F_{2} &{} 0 &{} E_{2}^{-} &{} 0\\ D_{2} &{} 0 &{} B_{2}^{+} &{} 0 &{} C_{2} &{} 0 &{} B_{2}^{-} &{} 0 &{} A_{2} \end{array}\right) \end{aligned}$$

(19)

where

$$\begin{aligned} A_{1}= & {} 153-16\Phi _{\text {de}}-(10-\Phi _{\text {ce}})\Phi _{\text {ce}}\\ B_{1}^{\pm }= & {} \left( -1+\Phi _{\text {ce}}\right) \left( 11+\Phi _{\text {ce}}\pm 12f(\alpha )\Gamma _{1}(t)\right) \\ C_{1}= & {} 32\left( 1+2\Phi _{\text {de}}+\Psi _{\text {de}}\right) \\ D_{1}^{\pm }= & {} 33\pm 64\Phi _{\text {de}}+\Phi _{\text {ce}}\left( 30+\Phi _{\text {ce}}\right) \\ E_{1}^{\pm }= & {} 2\left( 71+\left( 10-\Phi _{\text {ce}}\right) \Phi _{\text {ce}}\pm 4\Gamma _{1}(t)\left( 1+3\Phi _{\text {ce}}\right) f(\alpha )\right) \\ F_{1}= & {} 64\left( 1-\Psi _{\text {de}}\right) \\ G_{1}= & {} 2\left( 1-\Phi _{\text {ce}}\right) \left( 11+\Phi _{\text {ce}}\right) \\ H_{1}^{\pm }= & {} 153+16\Phi _{\text {de}}-\left( 10-\Phi _{\text {ce}}\right) \Phi _{\text {ce}}\pm 8\Gamma _{1}(t)\left( 1+3\Phi _{\text {ce}}\right) f(\alpha )\\ J_{1}= & {} 32\left( 1-2\Phi _{\text {de}}+\Psi _{\text {de}}\right) \\ K_{1}= & {} 4\left( 41-(10-\Phi _{\text {ce}})\Phi _{\text {ce}}\right) \end{aligned}$$

and

$$\begin{aligned} A_{2}= & {} 211+28\Phi _{\text {ce}}+17\Psi _{\text {ce}}\\ B_{2}^{\pm }= & {} -37+20\Phi _{\text {ce}}+17\Psi _{\text {ce}}\pm 12\left( \Gamma _{1}(t)-\Gamma _{3}(t)\right) f(\alpha )\\ C_{2}= & {} 2\left( 67+44\Phi _{\text {ce}}+17\Psi _{\text {ce}}\right) \\ D_{2}= & {} 188\Phi _{\text {ce}}+17\left( 3+\Psi _{\text {ce}}\right) \\ E_{2}^{\pm }= & {} 2\left( 157+20\Phi _{\text {ce}}-17\Psi _{\text {ce}}\pm 4\left( 3\Gamma _{3}(t)+5\Gamma _{1}(t)\right) f(\alpha )\right) \\ F_{2}= & {} 2\left( -3+20\Phi _{\text {ce}}-17\Psi _{\text {ce}}\right) \\ H_{2}= & {} 2\left( 37-20\Phi _{\text {ce}}-17\Psi _{\text {ce}}\right) \\ I_{2}^{\pm }= & {} 371-68\Phi _{\text {ce}}+17\Psi _{\text {ce}}\pm 8\left( 5\Gamma _{1}(t)+3\Gamma _{3}(t)\right) f(\alpha )\\ J_{2}^{\pm }= & {} 2\left( 27-44\Phi _{\text {ce}}+17\Psi _{\text {ce}}\pm 12\left( \Gamma _{1}(t)-\Gamma _{3}(t)\right) f(\alpha )\right) \\ K_{2}= & {} 17\left( 3-4\Phi _{\text {ce}}+\Psi _{\text {ce}}\right) \\ L_{2}= & {} 4\left( 67-20\Phi _{\text {ce}}+17\Psi _{\text {ce}}\right) \end{aligned}$$

with

$$\begin{aligned} f(\alpha )=-5+2\alpha . \end{aligned}$$