Multiparty quantum key agreement protocol based on locally indistinguishable orthogonal product states

Abstract

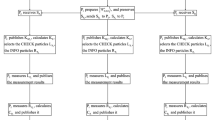
Based on locally indistinguishable orthogonal product states, we propose a novel multiparty quantum key agreement (QKA) protocol. In this protocol, the private key information of each party is encoded as some orthogonal product states that cannot be perfectly distinguished by local operations and classical communications. To ensure the security of the protocol with small amount of decoy particles, the different particles of each product state are transmitted separately. This protocol not only can make each participant fairly negotiate a shared key, but also can avoid information leakage in the maximum extent. We give a detailed security proof of this protocol. From comparison result with the existing QKA protocols, we can know that the new protocol is more efficient.

Appendix: a proof of Theorem 1

Proof

Now we prove the states (1) cannot be perfectly distinguished by LOCC if the first party goes first. If so, then by their symmetry these states cannot be perfectly distinguished with the second party going first.

Suppose that the first party performs a general measurement with a set of $3\times 3$ POVM elements $\{M^{\dag }_{k}M_{k};\,k=1,2,\ldots ,l_{1}\}$, where

$$\begin{aligned} \begin{aligned} M_{k}^{\dag }M_{k}= \left[ \begin{array}{ccc} m_{00}^{k} &{}\quad m_{01}^{k} &{}\quad m_{02}^{k}\\ m_{10}^{k} &{}\quad m_{11}^{k} &{}\quad m_{12}^{k}\\ m_{20}^{k} &{}\quad m_{21}^{k} &{}\quad m_{22}^{k} \end{array} \right] \end{aligned} \end{aligned}$$

under the basis $\{|0\rangle ,|1\rangle ,|2\rangle \}$.

It is noted that the postmeasurement states must be pairwise orthogonal for making further discrimination feasible. That is, the states that are orthogonal on the first side should maintain the orthogonality on the first side after the measurement.

For the states $|\psi _{1}\rangle$ and $|\psi _{5}\rangle$, we can get

$$\begin{aligned}&\langle \psi _{1}|M_{k}^{\dag }M_{k}\otimes (I_{3\times 3}^{\dag }I_{3\times 3})|\psi _{5}\rangle =0,\\&\langle \psi _{5}|M_{k}^{\dag }M_{k}\otimes (I_{3\times 3}^{\dag }I_{3\times 3})|\psi _{1}\rangle =0, \end{aligned}$$

i.e.,

$$\begin{aligned}&\frac{1}{2}[(\langle 0|+\langle 1|)M_{k}^{\dag }M_{k}|2\rangle ][\langle 1|I_{3\times 3}^{\dag } I_{3\times 3}(|0\rangle +|1\rangle )]=0,\\&\frac{1}{2}[\langle 2|M_{k}^{\dag }M_{k}(|0\rangle +|1\rangle )][(\langle 0|+\langle 1|)I_{3\times 3}^{\dag } I_{3\times 3}|1\rangle ]=0. \end{aligned}$$

Thus,

$$\begin{aligned}&m_{02}^{k}+m_{12}^{k}=0,\end{aligned}$$

(11)

$$\begin{aligned}&m_{20}^{k}+m_{21}^{k}=0. \end{aligned}$$

(12)

For the states $|\psi _{2}\rangle$ and $|\psi _{5}\rangle$, we can get

$$\begin{aligned}&\langle \psi _{2}|M_{k}^{\dag }M_{k}\otimes (I_{3\times 3}^{\dag }I_{3\times 3})|\psi _{5}\rangle =0,\\&\langle \psi _{5}|M_{k}^{\dag }M_{k}\otimes (I_{3\times 3}^{\dag }I_{3\times 3})|\psi _{2}\rangle =0, \end{aligned}$$

i.e.,

$$\begin{aligned}&\frac{1}{2}[(\langle 0|-\langle 1|)M_{k}^{\dag }M_{k}|2\rangle ][\langle 1|I_{3\times 3}^{\dag } I_{3\times 3}(|0\rangle +|1\rangle )]=0,\\&\frac{1}{2}[\langle 2|M_{k}^{\dag }M_{k}(|0\rangle -|1\rangle )][(\langle 0|+\langle 1|)I_{3\times 3}^{\dag } I_{3\times 3}|1\rangle ]=0. \end{aligned}$$

Thus,

$$\begin{aligned}&m_{02}^{k}-m_{12}^{k}=0,\end{aligned}$$

(13)

$$\begin{aligned}&m_{20}^{k}-m_{21}^{k}=0. \end{aligned}$$

(14)

So, we have

$$\begin{aligned} m_{02}^{k}=m_{12}^{k}=0 \end{aligned}$$

(15)

by Eqs. (11) and (13); and

$$\begin{aligned} m_{20}^{k}=m_{21}^{k}=0 \end{aligned}$$

(16)

by Eqs. (12) and (14).

For the states $|\psi _{3}\rangle$ and $|\psi _{7}\rangle$, we can get

$$\begin{aligned}&\langle \psi _{3}|M_{k}^{\dag }M_{k}\otimes (I_{3\times 3}^{\dag }I_{3\times 3})|\psi _{7}\rangle =0,\\&\langle \psi _{7}|M_{k}^{\dag }M_{k}\otimes (I_{3\times 3}^{\dag }I_{3\times 3})|\psi _{3}\rangle =0, \end{aligned}$$

i.e.,

$$\begin{aligned}&\frac{1}{2}[(\langle 0|+\langle 2|)M_{k}^{\dag }M_{k}|1\rangle ][\langle 2|I_{3\times 3}^{\dag } I_{3\times 3}(|0\rangle +|2\rangle )]=0,\\&\frac{1}{2}[\langle 1|M_{k}^{\dag }M_{k}(|0\rangle +|2\rangle )][(\langle 0|+\langle 2|)I_{3\times 3}^{\dag } I_{3\times 3}|2\rangle ]=0. \end{aligned}$$

Thus,

$$\begin{aligned}&m_{01}^{k}+m_{21}^{k}=0,\end{aligned}$$

(17)

$$\begin{aligned}&m_{10}^{k}+m_{12}^{k}=0. \end{aligned}$$

(18)

For the states $|\psi _{4}\rangle$ and $|\psi _{7}\rangle$, we can get

$$\begin{aligned}&\langle \psi _{4}|M_{k}^{\dag }M_{k}\otimes (I_{3\times 3}^{\dag }I_{3\times 3})|\psi _{7}\rangle =0,\\&\langle \psi _{7}|M_{k}^{\dag }M_{k}\otimes (I_{3\times 3}^{\dag }I_{3\times 3})|\psi _{4}\rangle =0, \end{aligned}$$

i.e.,

$$\begin{aligned}&\frac{1}{2}[(\langle 0|-\langle 2|)M_{k}^{\dag }M_{k}|1\rangle ][\langle 2|I_{3\times 3}^{\dag } I_{3\times 3}(|0\rangle +|2\rangle )]=0,\\&\frac{1}{2}[\langle 1|M_{k}^{\dag }M_{k}(|0\rangle -|2\rangle )][(\langle 0|+\langle 2|)I_{3\times 3}^{\dag } I_{3\times 3}|2\rangle ]=0. \end{aligned}$$

Thus,

$$\begin{aligned}&m_{01}^{k}-m_{21}^{k}=0,\end{aligned}$$

(19)

$$\begin{aligned}&m_{10}^{k}-m_{12}^{k}=0. \end{aligned}$$

(20)

So, we have

$$\begin{aligned} m_{01}^{k}=m_{21}^{k}=0 \end{aligned}$$

(21)

by Eqs. (17) and (19); and

$$\begin{aligned} m_{10}^{k}=m_{12}^{k}=0 \end{aligned}$$

(22)

by Eqs. (18) and (20).

For the states $|\psi _{1}\rangle$ and $|\psi _{2}\rangle$, we can get

$$\begin{aligned} \langle \psi _{1}|M_{k}^{\dag }M_{k}\otimes (I_{3\times 3}^{\dag }I_{3\times 3}) |\psi _{2}\rangle =0, \end{aligned}$$

i.e.,

$$\begin{aligned} \frac{1}{2}[(\langle 0|+\langle 1|)M_{k}^{\dag }M_{k}(|0\rangle -|1\rangle )][\langle 1|I_{3\times 3}^{\dag } I_{3\times 3}|1\rangle ]=0, \end{aligned}$$

Thus,

$$\begin{aligned} m_{00}^{k}-m_{01}^{k}+m_{10}^{k}-m_{11}^{k}=0. \end{aligned}$$

(23)

So, we have

$$\begin{aligned} m_{00}^{k}=m_{11}^{k} \end{aligned}$$

by Eqs. (21) and (22).

For the states $|\psi _{3}\rangle$ and $|\psi _{4}\rangle$, we can get

$$\begin{aligned} \langle \psi _{3}|M_{k}^{\dag }M_{k}\otimes (I_{3\times 3}^{\dag }I_{3\times 3})|\psi _{4}\rangle =0, \end{aligned}$$

i.e.,

$$\begin{aligned} \frac{1}{2}[(\langle 0|+\langle 2|)M_{k}^{\dag }M_{k}(|0\rangle -|2\rangle )][\langle 2|I_{3\times 3}^{\dag } I_{3\times 3}|2\rangle ]=0, \end{aligned}$$

Thus,

$$\begin{aligned} m_{00}^{k}-m_{02}^{k}+m_{20}^{k}-m_{22}^{k}=0. \end{aligned}$$

(24)

So, we have

$$\begin{aligned} m_{00}^{k}=m_{22}^{k} \end{aligned}$$

by Eqs. (15) and (16).

This means that any of the POVM elements of the first party should be in the form

$$\begin{aligned} \begin{aligned} M_{k}^{\dag }M_{k}= \left[ \begin{array}{ccc} m_{00}^{k} &{}\quad 0 &{}\quad 0\\ 0 &{}\quad m_{00}^{k} &{}\quad 0\\ 0 &{}\quad 0 &{}\quad m_{00}^{k} \end{array} \right] \end{aligned}. \end{aligned}$$

(25)

Consider the states $|\psi _{5}\rangle$ and $|\psi _{7}\rangle$. If the first party distinguishes the states outright then for one of states $|\psi _{5}\rangle$ and $|\psi _{7}\rangle$, $\langle \psi _{i}|M_{k}^{\dag }M_{k}\otimes (I_{3\times 3})^{\otimes 4}|\psi _{i}\rangle =0.$ But given (25), $\langle \psi _{i}|M_{k}^{\dag }M_{k}\otimes (I_{3\times 3})^{\otimes 4}|\psi _{i}\rangle =m_{00}^{k}.$ Thus, $m_{00}^{k}=0$ and, since POVM elements must be positive, $M_{k}^{\dag }M_{k}$ is the null matrix.

According to the above analysis, all of the first party’s POVM elements must be proportional to the identity. Thus, the first party cannot go first and by the symmetry of states (1), neither can the second party. Therefore, these states are locally indistinguishable. This completes the proof. $\square$