Entropic uncertainty relation under multiple bosonic reservoirs with filtering operator

Abstract

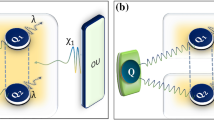
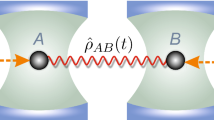
We study the dynamics of quantum-memory-assisted entropic uncertainty relation for an open quantum system of two qubits, which interact independently with their own multiple bosonic reservoirs at zero temperature. It is shown that the entropic uncertainty can be reduced with the increase in the number of reservoirs in both the weak and strong coupling regimes. This indicates a fact that the non-Markovianity may play a positive role in reducing entropic uncertainty. Furthermore, an unusual relation is found between the entropic uncertainty and mixedness of the quantum states. We finally reveal an effective manipulation of entropic uncertainty and mixedness by means of the local filtering operation.

Appendices

Appendix A: The detailed calculation process of Eq. (13)

Here, we will give a derivation of Eq. (13). By using Eqs. (7) and (12), we can obtain the analytical expression of $[F\otimes I]\rho _{AB}(t)[F\otimes I]^{\dagger }$ as

$$\begin{aligned}{}[F\otimes I]\rho _{AB}(t)[F\otimes I]^{\dagger }=&\,[(\sqrt{1-k}\left| 1\right\rangle \left\langle 1\right| +\sqrt{k}\left| 0\right\rangle \left\langle 0\right| )\otimes I](\rho _{11}(t)\left| 11\right\rangle \left\langle 11\right| \nonumber \\&+\rho _{14}(t)\left| 11\right\rangle \left\langle 00\right| +\rho _{22}(t)\left| 10\right\rangle \left\langle 10\right| \nonumber \\&+\rho _{33}(t)\left| 01\right\rangle \left\langle 01\right| +\rho _{41}(t)\left| 00\right\rangle \left\langle 11\right| \nonumber \\&+\rho _{44}(t)\left| 00\right\rangle \left\langle 00\right| )[(\sqrt{1-k}\left| 1\right\rangle \left\langle 1\right| +\sqrt{k}\left| 0\right\rangle \left\langle 0\right| )\otimes I]^{\dagger }. \end{aligned}$$

(14)

In virtue of the orthogonality relations that $\langle 1|1\rangle =\langle 0|0\rangle =1$ and $\langle 0|1\rangle =\langle 1|0\rangle =0$, ones have

$$\begin{aligned}{}[F\otimes I]\rho _{AB}(t)[F\otimes I]^{\dagger }=&\,\rho _{11}(t)(1-k)\left| 11\right\rangle \left\langle 11\right| +\rho _{14}(t)\sqrt{(1-k)k}\left| 11\right\rangle \left\langle 00\right| \nonumber \\&+\rho _{22}(t)(1-k)\left| 10\right\rangle \left\langle 10\right| +\rho _{33}(t)k\left| 01\right\rangle \left\langle 01\right| \nonumber \\&+\rho _{41}(t)\sqrt{(1-k)k}\left| 00\right\rangle \left\langle 11\right| +\rho _{44}(t)k\left| 00\right\rangle \left\langle 00\right| . \end{aligned}$$

(15)

Consequently, the trace of Eq. (15) can be evaluated easily as

$$\begin{aligned} Tr[[F\otimes I]\rho _{AB}(t)[F\otimes I]^{\dagger }]= & {} \rho _{11}(t)(1-k)+\rho _{22}(t)(1-k)\nonumber \\&+\,(\rho _{33}(t)+\rho _{44}(t))k . \end{aligned}$$

(16)

Finally, Eq. (13) is formulated by combining Eqs. (15)–(16) and the expressions of matrix elements in Eq. (7).

Appendix B

As a matter of fact, the time evolution of a single qubit subjected to the multiple bosonic reservoirs [44] can also be expressed by the following quantum dynamical map [53]

$$\begin{aligned}&|0\rangle _{S}|\bar{0}\rangle _{E}\rightarrow |0\rangle _{S}|\bar{0}\rangle _{E},\nonumber \\&|1\rangle _{S}|\bar{0}\rangle _{E}\rightarrow C_{1}(t)|1\rangle _{S}|\bar{0}\rangle _{E}+\sqrt{1-|C_{1}(t)|^{2}}|0\rangle _{S}|\bar{1}\rangle _{E}, \end{aligned}$$

(17)

where $C_{1}(t)$ is given by Eq. (5). $|\bar{0}\rangle _{E}$ and $|\bar{1}\rangle _{E}$ correspond to the vacuum state and the collective state containing only one excited mode of the multiple bosonic reservoirs, respectively.

For two identical quantum objects constrained by the same form of Hamiltonian as Eq. (3), when the global state of qubits A and B with their corresponding reservoirs a and b is prepared initially in

$$\begin{aligned} |\Phi (0)\rangle _{ABab}=|\psi (0)\rangle _{AB}\otimes |\bar{0}\bar{0}\rangle _{ab}, \end{aligned}$$

(18)

we can obtain its joint evolution with the help of Eq. (17), namely,

$$\begin{aligned} |\Phi (t)\rangle _{ABab}= & {} \frac{1}{\sqrt{2}}(|00\bar{0}\bar{0}\rangle +x_{1}|11\bar{0}\bar{0}\rangle +x_{2}|10\bar{0}\bar{1}\rangle +x_{3}|01\bar{1}\bar{0}\rangle \nonumber \\&+\,x_{4}|00\bar{1}\bar{1}\rangle )_{ABab}, \end{aligned}$$

(19)

where $|\psi (0)\rangle _{AB}$ is the Bell state of Eq. (6), and the relevant parameters in above equation are

$$\begin{aligned} x_{1}=C_{1}(t)^{2}, x_{2}=x_{3}=C_{1}(t)^{2}\sqrt{1-|C_{1}(t)|^{2}},x_{4}=1-|C_{1}(t)|^{2}. \end{aligned}$$

(20)

When the filtering operation is performed on qubit A of the total quantum state $|\Phi (t)\rangle _{ABab}$, the final state will evolve to

$$\begin{aligned} |\Psi (t)\rangle _{ABab}= & {} \frac{1}{\sqrt{2}}\{\sqrt{1-k}[x_{1}|11\bar{0}\bar{0}\rangle +x_{2}|10\bar{0}\bar{1}\rangle ] +\sqrt{k}[|00\bar{0}\bar{0}\rangle +x_{3}|01\bar{1}\bar{0}\rangle \nonumber \\&+\,x_{4}|00\bar{1}\bar{1}\rangle ]\}_{ABab}. \end{aligned}$$

(21)

By tracing the total evolved state $|\Phi (t)\rangle _{{ABab}}$ over the unrelated freedoms, the (unnormalized) reduced density matrices for two subsystems read

$$\begin{aligned} \rho _{ab}^{\Phi }=&\, Tr_{AB}[|\Phi (t)\rangle _{{ABab}{ABab}}\langle \Phi (t)|] \nonumber \\ =&\, \frac{1}{2}\{|x_{4}|^{2}|\bar{1}\bar{1}\rangle \langle \bar{1}\bar{1}| +|x_{3}|^{2}|\bar{1}\bar{0}\rangle \langle \bar{1}\bar{0}|+|x_{2}|^{2}|\bar{0} \bar{1}\rangle \langle \bar{0}\bar{1}|+(1+|x_{1}|^{2})|\bar{0}\bar{0}\rangle \langle \bar{0}\bar{0}|\nonumber \\&+x_{4}|\bar{1}\bar{1}\rangle \langle \bar{0}\bar{0}|+x_{4}^{*}|\bar{0}\bar{0}\rangle \langle \bar{1}\bar{1}|\}, \end{aligned}$$

(22)

$$\begin{aligned} \rho _{Ab}^{\Phi }=&\, Tr_{Ba}[|\Phi (t)\rangle _{{ABab}{ABab}}\langle \Phi (t)|] \nonumber \\ =&\, \frac{1}{2}\{|x_{2}|^{2}|1\bar{1}\rangle \langle 1\bar{1}| +|x_{1}|^{2}|1\bar{0}\rangle \langle 1\bar{0}|+|x_{4}|^{2}|0 \bar{1}\rangle \langle 0\bar{1}|+(1+|x_{3}|^{2})|0\bar{0}\rangle \langle 0\bar{0}|\nonumber \\&+x_{2}|1\bar{1}\rangle \langle 0\bar{0}|+x_{2}^{*}|0\bar{0}\rangle \langle 1\bar{1}|\},\end{aligned}$$

(23)

$$\begin{aligned} \rho _{Ba}^{\Phi }=&\, Tr_{Ab}[|\Phi (t)\rangle _{{ABab}{ABab}}\langle \Phi (t)|] \nonumber \\ =&\, \frac{1}{2}\{|x_{3}|^{2}|1\bar{1}\rangle \langle 1\bar{1}| +|x_{1}|^{2}|1\bar{0}\rangle \langle 1\bar{0}|+|x_{4}|^{2}|0\bar{1}\rangle \langle 0\bar{1}| +(1+|x_{2}|^{2})|0\bar{0}\rangle \langle 0\bar{0}|\nonumber \\&+x_{3}|1\bar{1}\rangle \langle 0\bar{0}| +x_{3}^{*}|0\bar{0}\rangle \langle 1\bar{1}|\}, \end{aligned}$$

(24)

$$\begin{aligned} \rho _{Aa}^{\Phi }=&\,Tr_{Bb}[|\Phi (t)\rangle _{{ABab}{ABab}}\langle \Phi (t)|] \nonumber \\ =&\,\frac{1}{2}\{(|x_{1}|^{2}+|x_{2}|^{2})|1\bar{0}\rangle \langle 1\bar{0}| +(|x_{3}|^{2}|+|x_{4}|^{2})|0\bar{1}\rangle \langle 0\bar{1}| +|0\bar{0}\rangle \langle 0\bar{0}|\nonumber \\&+(x_{1}x_{3}^{*}+x_{2}x_{4}^{*}) |1\bar{0}\rangle \langle 0\bar{1}|+(x_{1}^{*}x_{3}+x_{2}^{*}x_{4})|0\bar{1}\rangle \langle 1\bar{0}|\}. \end{aligned}$$

(25)

$$\begin{aligned} \rho _{Bb}^{\Phi }=&\,Tr_{Aa}[|\Phi (t)\rangle _{{ABab}{ABab}}\langle \Phi (t)|]\nonumber \\ =&\,\frac{1}{2}\{[|x_{1}|^{2}+|x_{3}|^{2}]|1\bar{0}\rangle \langle 1\bar{0}| +[|x_{2}|^{2}+|x_{4}|^{2}]|0\bar{1}\rangle \langle 0\bar{1}|+|0\bar{0}\rangle \langle 0\bar{0}|\nonumber \\&+[x_{1}x_{2}^{*}+x_{3}x_{4}^{*}]|1\bar{0}\rangle \langle 0\bar{1}|+[x_{2}x_{1}^{*}+x_{4}x_{3}^{*}]|0\bar{1}\rangle \langle 1\bar{0}|\}. \end{aligned}$$

(26)

$$\begin{aligned} \rho _{AB}^{\Phi }=&\,Tr_{ab}[|\Phi (t)\rangle _{{ABab}{ABab}}\langle \Phi (t)|]\nonumber \\ =&\,\frac{1}{2}\{|x_{1}|^{2}|11\rangle \langle 11| +|x_{3}|^{2}|01\rangle \langle 01|+|x_{2}|^{2}|10\rangle \langle 10|\nonumber \\&+(1+|x_{4}|^{2})|00\rangle \langle 00| +x_{1}^{*}|00\rangle \langle 11|+x_{1}|11\rangle \langle 00|\}. \end{aligned}$$

(27)

Meanwhile, the (unnormalized) reduced density matrices of two subsystems can also be obtained by tracing $|\Psi \rangle _{ABab}$ over the unrelated freedoms, i.e.,

$$\begin{aligned} \rho _{ab}^{\Psi }=&\,\frac{1}{2}\{k|x_{4}|^{2}|\bar{1}\bar{1}\rangle \langle \bar{1}\bar{1}| +k|x_{3}|^{2}|\bar{1}\bar{0}\rangle \langle \bar{1}\bar{0}|+|x_{2}|^{2}(1-k)|\bar{0} \bar{1}\rangle \langle \bar{0}\bar{1}|\nonumber \\&+(k+(1-k)|x_{1}|^{2})|\bar{0}\bar{0}\rangle \langle \bar{0}\bar{0}| +\sqrt{k}x_{4}|\bar{1}\bar{1}\rangle \langle \bar{0}\bar{0}|+\sqrt{k}x_{4}^{*}|\bar{0}\bar{0}\rangle \langle \bar{1}\bar{1}|\}, \end{aligned}$$

(28)

$$\begin{aligned} \rho _{Ab}^{\Psi }=&\,\frac{1}{2}\{(1-k)|x_{2}|^{2}|1\bar{1}\rangle \langle 1\bar{1}| +(1-k)|x_{1}|^{2}|1\bar{0}\rangle \langle 1\bar{0}|+k|x_{4}|^{2}|0\bar{1}\rangle \langle 0\bar{1}|\nonumber \\&+k(1+|x_{3}|^{2}) |0\bar{0}\rangle \langle 0\bar{0}|+\sqrt{k(1-k)}x_{2}|1\bar{1}\rangle \langle 0\bar{0}|+\sqrt{k(1-k)}x_{2}^{*}|0\bar{0}\rangle \langle 1\bar{1}|\}, \end{aligned}$$

(29)

$$\begin{aligned} \rho _{Ba}^{\Psi }=&\frac{1}{2}\{k|x_{3}|^{2}|1\bar{1}\rangle \langle 1\bar{1}| +(1-k)|x_{1}|^{2}|1\bar{0}\rangle \langle 1\bar{0}|+k|x_{4}|^{2}|0\bar{1}\rangle \langle 0\bar{1}|\nonumber \\&+(k+(1-k)|x_{2}|^{2}) |0\bar{0}\rangle \langle 0\bar{0}|+kx_{3}|1\bar{1}\rangle \langle 0\bar{0}|+kx_{3}^{*}|0\bar{0}\rangle \langle 1\bar{1}|\}, \end{aligned}$$

(30)

$$\begin{aligned} \rho _{Aa}^{\Psi }=&\,\frac{1}{2}\{(1-k)(|x_{1}|^{2}+|x_{2}|^{2})|1\bar{0}\rangle \langle 1\bar{0}| +k(|x_{3}|^{2}+|x_{4}|^{2})|0\bar{1}\rangle \langle 0\bar{1}| +k|0\bar{0}\rangle \langle 0\bar{0}|\nonumber \\&+\sqrt{k(1-k)}(x_{1}x_{3}^{*}+x_{2}x_{4}^{*})|1\bar{0}\rangle \langle 0\bar{1}|+\sqrt{k(1-k)}(x_{1}^{*}x_{3}+x_{2}^{*}x_{4})|0\bar{1}\rangle \langle 1\bar{0}|\}. \end{aligned}$$

(31)

$$\begin{aligned} \rho _{Bb}^{\Psi }=&\,\frac{1}{2}\{[(1-k)|x_{1}|^{2}+k|x_{3}|^{2}]|1\bar{0}\rangle \langle 1\bar{0}| +[(1-k)|x_{2}|^{2}+k|x_{4}|^{2}]|0\bar{1}\rangle \langle 0\bar{1}|\nonumber \\&+k|0\bar{0}\rangle \langle 0\bar{0}| +[(1-k)x_{1}x_{2}^{*}+kx_{3}x_{4}^{*}]|1\bar{0}\rangle \langle 0\bar{1}|+[(1-k)x_{2}x_{1}^{*}+kx_{4}x_{3}^{*}]|0\bar{1}\rangle \langle 1\bar{0}|\}. \end{aligned}$$

(32)

In addition, for the expression of $\rho _{AB}^{\Psi }$, please see Eq. (15).