Skip to main content
Springer Nature Link
Log in

One-step distillation of local-unitary-equivalent GHZ-type states

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

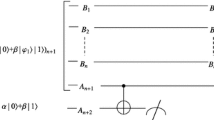
Abstract

Entanglement distillation plays a very important role in quantum information science. Distillation of high-purity Greenberger–Horne–Zeilinger (GHZ) states has been widely studied. We here show that a pure GHZ-type entangled state or its local unitary (LU)-equivalent state could be extracted from two copies of a particular multipartite mixed state (e.g., an X state) in a single step. Such one-step distillation schemes for LU-equivalent states are expected to shed light on mixed-state manipulation and purification, as well as establish a link between entanglement classification and distillation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Bennett, C.H., Brassard, G., Popescu, S., Schumacher, B., Smolin, J.A., Wootters, W.K.: Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76, 722–725 (1996)

    Article  ADS  Google Scholar 

  2. Bennett, C.H., DiVincenzo, D.P., Smolin, J.A., Wootters, W.K.: Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824–3851 (1996)

    Article  ADS  MathSciNet  Google Scholar 

  3. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  4. Pan, J.W., Chen, Z.B., Lu, C.Y., Weinfurter, H., Zeilinger, A., Żukowsk, M.: Multiphoton entanglement and interferometry. Rev. Mod. Phys. 84, 777–838 (2012)

    Article  ADS  Google Scholar 

  5. Pal, R., Bandyopadhyay, S., Ghosh, S.: Entanglement sharing through noisy qubit channels: one-shot optimal singlet fraction. Phys. Rev. A 90, 052304 (2014)

    Article  ADS  Google Scholar 

  6. Wallnöfer, J., Dür, W.: Measurement-based quantum communication with resource states generated by entanglement purification. Phys. Rev. A 95, 012303 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  7. Leditzky, F., Datta, N., Smith, G.: Useful states and entanglement distillation. arXiv preprint: arXiv:1701.03081 (2017)

  8. Chitambar, E., Hsieh, M.H.: Relating the resource theories of entanglement and quantum coherence. Phys. Rev. Lett. 117, 020402 (2016)

    Article  ADS  Google Scholar 

  9. Amico, L., Fazio, R., Osterloh, A., Vedral, V.: Entanglement in many-body systems. Rev. Mod. Phys. 80, 517–576 (2008)

    Article  ADS  MathSciNet  Google Scholar 

  10. Horodecki, M., Horodecki, P., Horodecki, R.: General teleportation channel, singlet fraction, and quasidistillation. Phys. Rev. A 60, 1888–1898 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  11. Tan, X., Zhang, X.: Controlled quantum secure direct communication by entanglement distillation or generalized measurement. Quantum Inf. Process. 15, 2137–2154 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  12. Deng, F.G., Long, G.L., Liu, X.S.: Two-step quantum direct communication protocol using the Einstein–Podolsky–Rosen pair block. Phys. Rev. A 68, 042317 (2003)

    Article  ADS  Google Scholar 

  13. Wang, X.W., Yang, G.J., Su, Y.H., Xie, M.: Simple schemes for quantum information processing with W-type entanglement. Quantum Inf. Process. 8, 431–442 (2009)

    Article  MathSciNet  Google Scholar 

  14. Wang, X.W., Zhang, D.Y., Yang, G.J., Tang, S.Q., Xie, L.J.: Remote information concentration and multipartite entanglement in multilevel systems. Phys. Rev. A 84, 042310 (2011)

    Article  ADS  Google Scholar 

  15. Sheng, Y.B., Zhou, L., Long, G.L.: Hybrid entanglement purification for quantum repeaters. Phys. Rev. A 88, 022302 (2013)

    Article  ADS  Google Scholar 

  16. Meng, F.X., Yu, X.T., Zhang, Z.C.: An economical state-dependent telecloning for a multiparticle GHZ state. Quantum Inf. Process. 17, 66 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  17. Murao, M., Plenio, M.B., Popescu, S., Vedral, V., Knight, P.L.: Multiparticle entanglement purification protocols. Phys. Rev. A 57, R4075–4078 (1998)

    Article  ADS  Google Scholar 

  18. Aschauer, H., Dür, W., Briegel, H.J.: Multiparticle entanglement purification for two-colorable graph states. Phys. Rev. A 71, 012319 (2005)

    Article  ADS  Google Scholar 

  19. Chen, K., Lo, H.K.: Multi-partite quantum cryptographic protocols with noisy GHZ states. Quantum Inf. Comput. 7, 689–715 (2007)

    MathSciNet  MATH  Google Scholar 

  20. Huber, M., Plesch, M.: Purification of genuine multipartite entanglement. Phys. Rev. A 83, 062321 (2011)

    Article  ADS  Google Scholar 

  21. Das, T., Kumar, A., Pal, A.K., Shukla, N., Sen(De), A., Sen, U.: Canonical distillation of entanglement. Phys. Lett. A 381, 3529–3535 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  22. Ruan, L., Dai, W., Win, M.Z.: Adaptive recurrence quantum entanglement distillation for two-Kraus-operator channels. arXiv preprint: arXiv:1706.07461 (2017)

  23. Fang, K., Wang, X., Tomamichel, M., Duan, R.: Non-asymptotic entanglement distillation. arXiv preprint arXiv:1706.06221 (2017)

  24. Krastanov, S., Albert, V.V., Jiang, L.: Optimized entanglement purification. arXiv preprint arXiv:1712.09762 (2017)

  25. Baghbanzadeh, S., Rezakhani, A.T.: Distillation of free entanglement from bound entangled states using weak measurements. Phys. Rev. A 88, 062320 (2013)

    Article  ADS  Google Scholar 

  26. Carle, T., Kraus, B., Dür, W., de Vicente, J.I.: Purification to locally maximally entangleable states. Phys. Rev. A 87, 012328 (2013)

    Article  ADS  Google Scholar 

  27. Chen, P.X., Liang, L.M., Li, C.Z., Huang, M.Q.: Necessary and sufficient condition for distillability with unit fidelity from finite copies of a mixed state: the most efficient purification protocol. Phys. Rev. A 66, 022309 (2002)

    Article  ADS  MathSciNet  Google Scholar 

  28. Chen, P.X., Li, C.Z.: Distilling multipartite pure states from a finite number of copies of multipartite mixed states. Phys. Rev. A 69, 012308 (2004)

    Article  ADS  Google Scholar 

  29. Czechlewski, M., Grudka, A., Ishizaka, S., Wójcik, A.: Entanglement purification protocol for a mixture of a pure entangled state and a pure product state. Phys. Rev. A 80, 014303 (2009)

    Article  ADS  Google Scholar 

  30. Wang, X.W., Tang, S.Q., Yuan, J.B., Zhang, D.Y.: Distilling perfect GHZ states from two copies of non-GHZ-diagonal mixed states. Opt. Commun. 392, 185–189 (2017)

    Article  ADS  Google Scholar 

  31. Dür, W., Vidal, G., Cirac, J.I.: Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 62, 062314 (2000)

    Article  ADS  MathSciNet  Google Scholar 

  32. Kraus, B.: Local unitary equivalence and entanglement of multipartite pure states. Phys. Rev. A 82, 032121 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  33. Liu, B., Li, J.L., Li, X., Qiao, C.F.: Local unitary classification of arbitrary dimensional multipartite pure states. Phys. Rev. Lett. 108, 050501 (2012)

    Article  ADS  Google Scholar 

  34. Greenberger, D.M., Horne, M.A., Shimony, A., Zeilinger, A.: Bells theorem without inequalities. Am. J. Phys. 58, 1131–1143 (1990)

    Article  ADS  MathSciNet  Google Scholar 

  35. Hillery, M., Bužek, V., Berthiaume, A.: Quantum secret sharing. Phys. Rev. A 59, 1829–1834 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  36. Xiao, L., Long, G.L., Deng, F.G., Pan, J.W.: Efficient multiparty quantum-secret-sharing schemes. Phys. Rev. A 69, 052307 (2004)

    Article  ADS  Google Scholar 

  37. Deng, F.G., Li, C.Y., Li, Y.S., Zhou, H.Y., Wang, Y.: Symmetric multiparty-controlled teleportation of an arbitrary two-particle entanglement. Phys. Rev. A 72, 022338 (2005)

    Article  ADS  Google Scholar 

  38. Yu, Y.F., Feng, J., Zhan, M.S.: Remote information concentration by a Greenberger–Horne–Zeilinger state and by a bound entangled state. Phys. Rev. A 68, 024303 (2003)

    Article  ADS  Google Scholar 

  39. Cunha, M.M., Fonseca, E.A., Moreno, M.G.M., Parisio, F.: Non-ideal teleportation of tripartite entanglement: Einstein–Podolsky–Rosen versus Greenberger–Horne–Zeilinger schemes. Quantum Inf. Process. 16, 254 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  40. Joy, D., Surendran, S.P., Sabir, M.: Efficient deterministic secure quantum communication protocols using multipartite entangled states. Quantum Inf. Process. 16, 157 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  41. Zhang, W., Qiu, D., Zou, X., Mateus, P.: Analyses and improvement of a broadcasting multiple blind signature scheme based on quantum GHZ entanglement. Quantum Inf. Process. 16, 150 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  42. Martins, A.M.: Necessary and sufficient conditions for local unitary equivalence of multiqubit states. Phys. Rev. A 91, 042308 (2015)

    Article  ADS  Google Scholar 

  43. Yu, T., Eberly, J.H.: Evolution from entanglement to decoherence of bipartite mixed “X” states. Quantum Inf. Comput. 7, 459 (2007)

    MathSciNet  MATH  Google Scholar 

  44. Hashemi Rafsanjani, S.M., Huber, M., Broadbent, C.J., Eberly, J.H.: Genuinely multipartite concurrence of N-qubit X matrices. Phys. Rev. A 86, 062303 (2012)

    Article  ADS  Google Scholar 

  45. Qu, C.C., Zhou, L., Sheng, Y.B.: Entanglement concentration for concatenated Greenberger–Horne–Zeilinger state. Quantum Inf. Process. 14, 4131–4146 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  46. Shukla, C., Banerjee, A., Pathak, A.: Protocols and quantum circuits for implementing entanglement concentration in cat state, GHZ-like state and nine families of 4-qubit entangled states. Quantum Inf. Process. 14, 2077–2099 (2015)

    Article  ADS  Google Scholar 

  47. Pan, J., Zhou, L., Gu, S.P., Wang, X.F., Sheng, Y.B., Wang, Q.: Efficient entanglement concentration for concatenated Greenberger–Horne–Zeilinger state with the cross-Kerr nonlinearity. Quantum Inf. Process. 15, 1669–1687 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  48. Nielsen, M., Chuang, I.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  49. Wang, X.W., Yu, S., Zhang, D.Y., Oh, C.H.: Effect of weak measurement on entanglement distribution over noisy channels. Sci. Rep. 6, 22408 (2016)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the NSFC (Gant No. 11647129), the Scientific Research Fund of Hunan Provincial Education Department (Grant Nos. 15A028 and 16B036), the HNNSF (Grant Nos. 2016JJ2009 and 2017JJ3005), the Science and Technology Plan Project of Hunan Province (2016TP1020), Open Fund Project of Hunan Provincial Key Laboratory of Intelligent Information Processing and Application for Hengyang Normal University (IIPA18K07), and Opening Fund of Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of Ministry of Education (QSQC1702).

Author information

Authors and Affiliations

  1. College of Physics and Electronic Engineering, and Hunan Provincial Key Laboratory of Intelligent Information Processing and Application, Hengyang Normal University, Hengyang, 421002, China

    Jibing Yuan, Shiqing Tang, Xinwen Wang & Dengyu Zhang

  2. Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of Ministry of Education, Hunan Normal University, Changsha, 410081, China

    Xinwen Wang

Authors
  1. Jibing Yuan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Shiqing Tang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Xinwen Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Dengyu Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xinwen Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yuan, J., Tang, S., Wang, X. et al. One-step distillation of local-unitary-equivalent GHZ-type states. Quantum Inf Process 17, 259 (2018). https://doi.org/10.1007/s11128-018-2034-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-018-2034-3

Keywords