Abstract
We address the problem of unambiguous discrimination of quantum channels (UDQC) without entanglement. As our main result, we show that even in the absence of entanglement, partial UDQC (PUDQC) can still be performed—depending on the unknown given channel. We provide a necessary and sufficient condition for PUDQC and put forth a method to perform the PUDQC once the said condition is met. We propose the performance metrics that capture the expected performance of the PUDQC independent of the specific channels to be distinguished. Finally, we perform PUDQC on several qubit channel pairs as concrete examples and derive the proposed performance metrics for these channel pairs.





Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
Unambiguous discrimination refers to the scenario where the margin of error is zero in the announced result. Such methods of unambiguous discrimination in quantum state discrimination are obtained at the expense of allowing a nonzero probability of inconclusive results at the end of the protocol.
This parameterization has a minor difference from standard parameterization on the Bloch sphere and leads to some redundant pairs of \(\phi \) and \(\theta \) values. We have made this choice because later in the article, we fix \(\phi = 0\), then the range of \(0 \le \theta \le 2\pi \) allows us to cover a whole circle in the X–Z plane.
A Bloch vector
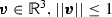 defines the location of a (possibly mixed) qubit in the Bloch sphere (ball). The density matrix corresponding to a Bloch vector is given by
defines the location of a (possibly mixed) qubit in the Bloch sphere (ball). The density matrix corresponding to a Bloch vector is given by  .
.We consider when \(\mathcal {N}_1\) is distinguishable from \(\mathcal {N}_2\). The other way round can be obtained using the same reasoning.
In fact we can choose
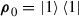 as well. The decisive event, then, will be observing the state \(|0\rangle \) at the output of the channel. This will not change the optimal POVMs and the value of \(\epsilon \).
as well. The decisive event, then, will be observing the state \(|0\rangle \) at the output of the channel. This will not change the optimal POVMs and the value of \(\epsilon \).
References
Xie, Y., Li, J., Malaney, R., Yuan, J.: Channel identification and its impact on quantum LDPC code performance. In: 2012 Australian Communications Theory Workshop (AusCTW), pp. 140–144 (2012)
ur Rehman, J., Qaisar, S., Jeong, Y., Shin, H.: Security of a control key in quantum key distribution. Mod. Phys. Lett. B 31(11), 1750119 (2017)
Qaisar, S., ur Rehman, J., Jeong, Y., Shin, H.: Practical deterministic secure quantum communication in a lossy channel. Prog. Theor. Exp. Phys. 2017(4), 041A01 (2017)
Shaham, A., Halevy, A., Dovrat, L., Megidish, E., Eisenberg, H.S.: Entanglement dynamics in the presence of controlled unital noise. Sci. Rep. 5, 10796 (2015)
Fischer, D.G., Mack, H., Cirone, M.A., Freyberger, M.: Enhanced estimation of a noisy quantum channel using entanglement. Phys. Rev. A 64, 022309 (2001)
Fujiwara, A., Imai, H.: Quantum parameter estimation of a generalized Pauli channel. J. Phys. A Math. Gen. 36(29), 8093 (2003)
Ji, Z., Wang, G., Duan, R., Feng, Y., Ying, M.: Parameter estimation of quantum channels. IEEE Trans. Inf. Theory 54(11), 5172–5185 (2008)
Hayashi, M.: Quantum channel estimation and asymptotic bound. J. Phys. Conf. Ser. 233(1), 012016 (2010)
Frey, M., Collins, D., Gerlach, K.: Probing the qudit depolarizing channel. J. Phys. A Math. Theor. 44(20), 205306 (2011)
Ruppert, L., Virosztek, D., Hangos, K.: Optimal parameter estimation of Pauli channels. J. Phys. A Math. Theor. 45(26), 265305 (2012)
Collins, D., Stephens, J.: Depolarizing-channel parameter estimation using noisy initial states. Phys. Rev. A 92, 032324 (2015)
Suzuki, J.: Entanglement detection and parameter estimation of quantum channels. Phys. Rev. A 94, 042306 (2016)
Acín, A.: Statistical distinguishability between unitary operations. Phys. Rev. Lett. 87, 177901 (2001)
Chiribella, G., D’Ariano, G.M., Sacchi, M.F.: Optimal estimation of group transformations using entanglement. Phys. Rev. A 72, 042338 (2005)
Chiribella, G., D’Ariano, G.M., Perinotti, P.: Memory effects in quantum channel discrimination. Phys. Rev. Lett. 101, 180501 (2008)
Li, L., Qiu, D.: Optimal discrimination between quantum operations. J. Phys. A Math. Theor. 41(33), 335302 (2008)
Matthews, W., Piani, M., Watrous, J.: Entanglement in channel discrimination with restricted measurements. Phys. Rev. A 82, 032302 (2010)
Harrow, A.W., Hassidim, A., Leung, D.W., Watrous, J.: Adaptive versus nonadaptive strategies for quantum channel discrimination. Phys. Rev. A 81, 032339 (2010)
Wang, Y.M., Li, J.G., Zou, J., Xu, B.M.: Quantum process discrimination with information from environment. Chin. Phys. B 25(12), 120302 (2016)
Takeoka, M., Wilde, M.M.: Optimal estimation and discrimination of excess noise in thermal and amplifier channels. arxiv:1611.09165 (2016)
Chattopadhyay, I., Sarkar, D.: Distinguishing quantum operations: LOCC versus separable operators. Int. J. Quantum Inf. 14(06), 1640028 (2016)
Puzzuoli, D., Watrous, J.: Ancilla dimension in quantum channel discrimination. Ann. Henri Poincaré 18(4), 1153–1184 (2017)
Pirandola, S., Lupo, C.: Ultimate precision of adaptive noise estimation. Phys. Rev. Lett. 118, 100502 (2017)
Wang, G., Ying, M.: Unambiguous discrimination among quantum operations. Phys. Rev. A 73, 042301 (2006)
Duan, R., Feng, Y., Ying, M.: Perfect distinguishability of quantum operations. Phys. Rev. Lett. 103, 210501 (2009)
Wu, X., Duan, R.: Exact quantum search by parallel unitary discrimination schemes. Phys. Rev. A 78, 012303 (2008)
Lu, C., Chen, J., Duan, R.: Some bounds on the minimum number of queries required for quantum channel perfect discrimination. Quantum Inf. Comput. 12(1–2), 138–148 (2012)
Duan, R., Guo, C., Li, C.K., Li, Y.: Parallel distinguishability of quantum operations. In: 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, pp. 2259–2263 (2016)
Aharonov, D., Kitaev, A., Nisan, N.: Quantum circuits with mixed states. In: Proceedings of the 30th Annual ACM Symposium on Theory of Computing (STOC ’98), Dallas, TX, USA, pp. 23–30 (1998)
Yuan, H., Fung, C.H.F.: Fidelity and Fisher information on quantum channels. New J. Phys. 19(11), 113039 (2017)
Lü-Jun, L.: Ambiguous discrimination of general quantum operations. Commun. Theor. Phys. 62(6), 813 (2014)
Chiribella, G., D’Ariano, G.M., Perinotti, P.: Quantum circuit architecture. Phys. Rev. Lett. 101, 060401 (2008)
Audenaert, K.M.R., Calsamiglia, J., noz Tapia, R.M., Bagan, E., Masanes, L., Acín, A., Verstraete, F.: Discriminating states: the quantum Chernoff bound. Phys. Rev. Lett. 98, 160501 (2007)
Calsamiglia, J., noz Tapia, R.M., Masanes, L., Acín, A., Bagan, E.: Quantum Chernoff bound as a measure of distinguishability between density matrices: application to qubit and Gaussian states. Phys. Rev. A 77, 032311 (2008)
Brandão, F.G.S.L., Plenio, M.B.: A generalization of quantum Stein’s lemma. Commun. Math. Phys. 295(3), 791–828 (2010)
Cooney, T., Mosonyi, M., Wilde, M.M.: Strong converse exponents for a quantum channel discrimination problem and quantum-feedback-assisted communication. Commun. Math. Phys. 344(3), 797–829 (2016)
Berta, M., Brandão, F.G.S.L., Hirche, C.: On composite quantum hypothesis testing. arxiv:1709.07268 (2017)
Bae, J., Kwek, L.C.: Quantum state discrimination and its applications. J. Phys. A Math. Theor. 48(8), 083001 (2015)
Cohen, S.M.: Class of unambiguous state discrimination problems achievable by separable measurements but impossible by local operations and classical communication. Phys. Rev. A 91, 012321 (2015)
Yuan, H., Fung, C.H.F.: Quantum metrology matrix. Phys. Rev. A 96, 012310 (2017)
Yuan, H., Fung, C.H.F.: Quantum parameter estimation with general dynamics. NPJ Quantum Inform. 3(1), 14 (2017)
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No. 2016R1A2B2014462) and ICT R&D program of MSIP/IITP [R0190-15-2030, Reliable crypto-system standards and core technology development for secure quantum key distribution network].
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
About this article
Cite this article
ur Rehman, J., Farooq, A., Jeong, Y. et al. Quantum channel discrimination without entanglement. Quantum Inf Process 17, 271 (2018). https://doi.org/10.1007/s11128-018-2037-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-018-2037-0



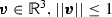 defines the location of a (possibly mixed) qubit in the Bloch sphere (ball). The density matrix corresponding to a Bloch vector is given by
defines the location of a (possibly mixed) qubit in the Bloch sphere (ball). The density matrix corresponding to a Bloch vector is given by  .
.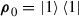 as well. The decisive event, then, will be observing the state
as well. The decisive event, then, will be observing the state