Skip to main content

Advertisement

Springer Nature Link
Log in

Exploring uncertainty relation and its connection with coherence under the Heisenberg spin model with the Dzyaloshinskii–Moriya interaction

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

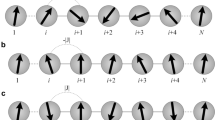
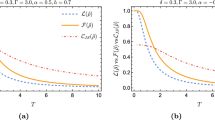
Uncertainty principle is at the heart of quantum physics, taking a fundamental and crucial role in the area of quantum information science, and it provides a remarkable lower bound to quantify our prediction for the measured outcome of two incompatible observables. Herein, the relationship between the lower bound of the measured uncertainty and quantum coherence is investigated under a one-dimensional Heisenberg XXZ spin model with Dzyaloshinskii–Moriya (DM) interactions, and the effect of DM interaction on the entropic uncertainty is also examined in details. We reveal the systematic temperature can give rise to the increase in the measurement uncertainty of interest at thermal equilibrium. By contrast, the stronger coupling strength \( \left| J \right| \) or the stronger DM interaction would induce the decrease in the amount with respect to the uncertainty. Moreover, we analyze the dynamical behaviors of quantum coherence and find that the bound of the uncertainty is oppositely correlated with the quantum coherence dramatically. Further, the effects of DM interaction along x-direction (characterized by the parameter Dx) and z-direction (characterized by Dz) on the uncertainty of interest are discussed, respectively. For the antiferromagnetic frame J > 0, it is interesting to obtain that x-direction DM interaction Dx exhibits a more powerful influence on reducing the uncertainty and enhancing the systematic coherence, when comparing with that of Dz. With these in mind, we wish our investigations would better understand the dynamical features of the measured uncertainty in the spin-based solid systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Heisenberg, W.: Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 43, 172 (1927)

    Article  ADS  Google Scholar 

  2. Kennard, E.H.: Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 44, 326 (1927)

    Article  ADS  Google Scholar 

  3. Robertson, H.P.: Violation of Heisenberg’s uncertainty principle. Phys. Rev. 34, 163 (1929)

    Article  ADS  Google Scholar 

  4. Deutsch, D.: Uncertainty in quantum measurements. Phys. Rev. Lett. 50, 631–633 (1983)

    Article  ADS  MathSciNet  Google Scholar 

  5. Kraus, K.: Complementary observables and uncertainty relations. Phys. Rev. D 35, 3070 (1987)

    Article  ADS  MathSciNet  Google Scholar 

  6. Maassen, H., Uffink, J.B.M.: Generalized entropic uncertainty relations. Phys. Rev. Lett. 60, 1103 (1988)

    Article  ADS  MathSciNet  Google Scholar 

  7. Berta, M., Christandl, M., Colbeck, R., Renes, J.M., Renner, R.: The uncertainty principle in the presence of quantum memory. Nat. Phys. 6, 659–662 (2010)

    Article  Google Scholar 

  8. Nielson, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2002)

    Google Scholar 

  9. Li, C.F., Xu, X.Y., Li, K., Guo, G.C.: Experimental investigation of the entanglement-assisted entropic uncertainty principle. Nat. Phys. 7, 752 (2011)

    Article  Google Scholar 

  10. Tomamichel, M., Renner, R.: The uncertainty relation for smooth entropies. Phys. Rev. Lett. 106, 110506 (2011)

    Article  ADS  Google Scholar 

  11. Zhang, J., Zhang, Y., Yu, C.S.: Rényi entropy uncertainty relation for successive projective measurements. Quantum Inf. Process. 14, 2239 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  12. Coles, P.J., Colbeck, R., Yu, L., Zwolak, M.: Uncertainty relations from simple entropic properties. Phys. Rev. Lett. 108, 210405 (2012)

    Article  ADS  Google Scholar 

  13. Baek, K., Son, W.: Unsharpness of generalized measurement and its effects in entropic uncertainty relations. Sci. Rep. 6, 30228 (2016)

    Article  ADS  Google Scholar 

  14. Pati, A.K., Wilde, M.M., Usha Devi, A.R., Rajagopal, A.K.: Quantum discord and classical correlation can tighten the uncertainty principle in the presence of quantum memory. Phys. Rev. A 86, 042105 (2012)

    Article  ADS  Google Scholar 

  15. Coles, P.J., Piani, M.: Improved entropic uncertainty relations and information exclusion relations. Phys. Rev. A 89, 022112 (2014)

    Article  ADS  Google Scholar 

  16. Pramanik, T., Mal, S., Majumdar, A.S.: Lower bound of quantum uncertainty from extractable classical information. Quantum Inf. Process. 15, 981–999 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  17. Adabi, F., Salimi, S., Haseli, S.: Tightening the entropic uncertainty bound in the presence of quantum memory. Phys. Rev. A 93, 062123 (2016)

    Article  ADS  Google Scholar 

  18. Hu, M.L., Fan, H.: Quantum-memory-assisted entropic uncertainty principle, teleportation and entanglement witness in structured reservoirs. Phys. Rev. A 86, 032338 (2012)

    Article  ADS  Google Scholar 

  19. Hu, M.L., Fan, H.: Competition between quantum correlations in the quantum-memory-assisted entropic uncertainty relation. Phys. Rev. A 87, 022314 (2013)

    Article  ADS  Google Scholar 

  20. Hu, M.L., Fan, H.: Upper bound and shareability of quantum discord based on entropic uncertainty relations. Phys. Rev. A 88, 014105 (2013)

    Article  ADS  Google Scholar 

  21. Vallone, G., Marangon, D.G., Tomasin, M., Villoresi, P.: Quantum randomness certified by the uncertainty principle. Phys. Rev. A 90, 052327 (2014)

    Article  ADS  Google Scholar 

  22. Miller, C.A., Shi, Y.: Proceedings of the Forty-Sixth Annual ACM Symposium on Theory of Computing, pp. 417–426. American Mathematical Society, New York (2014)

    Google Scholar 

  23. Koenig, R., Wehner, S., Wullschleger, J.: Unconditional security from noisy quantum storage. IEEE Trans. Inf. Theory 58, 1962–1984 (2012)

    Article  MathSciNet  Google Scholar 

  24. Dupuis, F., Fawzi, O., Wehner, S.: Entanglement sampling and applications. IEEE Trans. Inf. Theory 61, 1093 (2015)

    Article  MathSciNet  Google Scholar 

  25. Jarzyna, M., Demkowicz-Dobrzański, R.: True precision limits in quantum metrology. New J. Phys. 17, 013010 (2015)

    Article  ADS  Google Scholar 

  26. Grosshans, F., Cerf, N.J.: Continuous-variable quantum cryptography is secure against non-Gaussian attacks. Phys. Rev. Lett. 92, 047905 (2004)

    Article  ADS  Google Scholar 

  27. Cerf, N.J., Bourennane, M., Karlsson, A., Gisin, N.: Security of Quantum key distribution using d-level systems. Phys. Rev. Lett. 88, 127902 (2002)

    Article  ADS  Google Scholar 

  28. Shi, J.D., Ding, Z.Y., Wu, T., He, J., Yu, L.Z., Sun, W.Y., Wang, D., Ye, L.: Entanglement witness via quantum-memory-assisted entropic uncertainty relation. Laser Phys. Lett. 14, 125208 (2017)

    Article  ADS  Google Scholar 

  29. Bennett, C.H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 70, 1895 (1993)

    Article  ADS  MathSciNet  Google Scholar 

  30. Zou, H.M., Fang, M.F., Yang, B.Y., Guo, Y.N., He, W., Zhang, S.Y.: The quantum entropic uncertainty relation and entanglement witness in the two-atom system coupling with the non-Markovian environments. Phys. Scr. 89, 115101 (2014)

    Article  ADS  Google Scholar 

  31. Zhang, Y.L., Fang, M.F., Kang, G.D., Zhou, Q.P.: Reducing quantum-memory-assisted entropic uncertainty by weak measurement and weak measurement reversal. Int. J. Quantum Inf. 13, 1550037 (2015)

    Article  Google Scholar 

  32. Jia, L.J., Tian, Z.H., Jing, J.L.: Entropic uncertainty relation in de Sitter space. Ann. Phys. 353, 37–47 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  33. Xu, Z.Y., Yang, W.L., Feng, M.: Quantum-memory-assisted entropic uncertainty relation under noise. Phys. Rev. A 86, 012113 (2012)

    Article  ADS  Google Scholar 

  34. Yao, C.M., Chen, Z.H., Ma, Z.H., Severini, S., Serafini, A.: Entanglement and discord assisted entropic uncertainty relations under decoherence. Sci. China Phys. Mech. Astron. 57, 1703–1711 (2014)

    Article  ADS  Google Scholar 

  35. Wang, D., Ming, F., Huang, A.J., Sun, W.Y., Shi, J.D., Ye, L.: Exploration of quantum-memory-assisted entropic uncertainty relations in a noninertial frame. Laser Phys. Lett. 14, 055205 (2017)

    Article  ADS  Google Scholar 

  36. Feng, J., Zhang, Y.Z., Gould, M.D., Fan, H.: Entropic uncertainty relations under the relativistic motion. Phys. Lett. B 726, 527–532 (2013)

    Article  ADS  Google Scholar 

  37. Ming, F., Wang, D., Huang, A.J., Sun, W.Y., Shi, J.D., Ye, L.: Decoherence effect on quantum-memory-assisted entropic uncertainty relations. Quantum Inf. Process. 17, 9 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  38. Huang, A.J., Shi, J.D., Wang, D., Ye, L.: Steering quantum-memory-assisted entropic uncertainty under unital and nonunital noises via filtering operations. Quantum Inf. Process. 16, 46 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  39. Zhang, G.F., Li, S.S.: Thermal entanglement in a two-qubit Heisenberg XXZ spin chain under an inhomogeneous magnetic field. Phys. Rev. A 72, 034302 (2005)

    Article  ADS  Google Scholar 

  40. Shi, J.D., Wang, D., Ye, L.: Genuine multipartite entanglement as the indicator of quantum phase transition in spin system. Quantum Inf. Process. 15, 4629–4640 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  41. Liang, Q.: Quantum correlations in a two-qubit Heisenberg XX model under intrinsic decoherence. Commun. Theor. Phys. 60, 391 (2013)

    Article  Google Scholar 

  42. Asoudeh, M., Karimipour, V.: Thermal entanglement of spins in an inhomogeneous magnetic field. Phys. Rev. A 71, 022308 (2005)

    Article  ADS  Google Scholar 

  43. Mahdavifar, S., Mahdavifar, S., Jafari, R.: Magnetic quantum correlations in the one-dimensional transverse-field XXZ model. Phys. Rev. A 96, 052303 (2017)

    Article  ADS  Google Scholar 

  44. Wang, D., Ming, F., Huang, A.J., Sun, W.Y., Ye, L.: Entropic uncertainty for spin-1/2 XXX chains in the presence of inhomogeneous magnetic fields and its steering via weak measurement reversals. Laser Phys. Lett. 14, 095204 (2017)

    Article  ADS  Google Scholar 

  45. Huang, A.J., Wang, D., Wang, J.M., Shi, J.D., Sun, W.Y., Ye, L.: Exploring entropic uncertainty relation in the Heisenberg XX model with inhomogeneous magnetic field. Quantum Inf. Process. 16, 204 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  46. Wang, D., Huang, A.J., Ming, F., Sun, W.Y., Lu, H.P., Liu, C.C., Ye, L.: Quantum-memory-assisted entropic uncertainty relation in a Heisenberg XYZ chain with an inhomogeneous magnetic field. Laser Phys. Lett. 14, 065203 (2017)

    Article  ADS  Google Scholar 

  47. Wootters, W.K.: Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248 (1998)

    Article  ADS  Google Scholar 

  48. Huang, Z.M., Tian, Z.H.: Dynamics of quantum entanglement in de Sitter spacetime and thermal Minkowski spacetime. Nucl. Phys. B 923, 458–474 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  49. Chen, J.L., Deng, D.L., Su, H.Y., Wu, C.F., Oh, C.H.: Detecting full N-particle entanglement in arbitrarily-high-dimensional systems with Bell-type inequalities. Phys. Rev. A 83, 022316 (2011)

    Article  ADS  Google Scholar 

  50. Chen, J.L., Ren, C.L., Chen, C.B., Ye, X.J., Pati, A.K.: Bell’s nonlocality can be detected by the violation of Einstein–Podolsky–Rosen steering inequality. Sci. Rep. 6, 39063 (2016)

    Article  ADS  Google Scholar 

  51. Jiang, S.H., Xu, Z.P., Su, H.Y., Pati, A.K., Chen, J.L.: Generalized Hardy’s paradox. Phys. Rev. Lett. 120, 050403 (2018)

    Article  ADS  Google Scholar 

  52. Sun, K., Ye, X.J., Xu, J.S., Xu, X.Y., Tang, J.S., Wu, Y.C., Chen, J.L., Li, C.F., Guo, G.C.: Experimental quantification of asymmetric Einstein–Podolsky–Rosen steering. Phys. Rev. Lett. 116, 160404 (2016)

    Article  ADS  Google Scholar 

  53. Wang, J.C., Cao, H.X., Jing, J.L., Fan, H.: Gaussian quantum steering and its asymmetry in curved spacetime. Phys. Rev. D 93, 125011 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  54. Baumgratz, T., Cramer, M., Plenio, M.B.: Quantifying coherence. Phys. Rev. Lett. 113, 140401 (2014)

    Article  ADS  Google Scholar 

  55. Zurek, W.K.: Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 75, 715 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  56. Yu, C.S.: Quantum coherence via skew information and its polygamy. Phys. Rev. A 95, 042337 (2017)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Science Foundation of China under Grant Nos. 61601002 and 11575001, Anhui Provincial Natural Science Foundation (Grant No. 1508085QF139), the Key Research Foundation of Education Ministry of Anhui Province of China (Grant No. KJ2015A041) and the fund from CAS Key Laboratory of Quantum Information (Grant No. KQI201701).

Author information

Authors and Affiliations

  1. School of Physics and Material Science, Anhui University, Hefei, 230601, China

    Fei Ming, Dong Wang, Wei-Nan Shi, Ai-Jun Huang, Ming-Ming Du, Wen-Yang Sun & Liu Ye

  2. CAS Key Laboratory of Quantum Information, University of Science and Technology of China, Hefei, 230026, China

    Dong Wang

Authors
  1. Fei Ming
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Dong Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Wei-Nan Shi
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Ai-Jun Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Ming-Ming Du
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Wen-Yang Sun
    View author publications

    You can also search for this author inPubMed Google Scholar

  7. Liu Ye
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Dong Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ming, F., Wang, D., Shi, WN. et al. Exploring uncertainty relation and its connection with coherence under the Heisenberg spin model with the Dzyaloshinskii–Moriya interaction. Quantum Inf Process 17, 267 (2018). https://doi.org/10.1007/s11128-018-2038-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-018-2038-z

Keywords