Skip to main content

Advertisement

Springer Nature Link
Log in

The randomness in 2\(\rightarrow \)1 quantum random access code without a shared reference frame

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

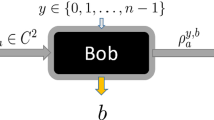
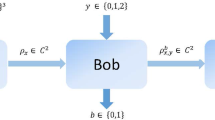
The non-classical correlations presented in quantum random access code experiment are a powerful diagnostic tool for semi-device-independent random number generator protocols. The idea behind it is that if the user observes the optimal non-classical correlations, he has the guarantee that the unknown quantum states and measurements in the devices have carefully calibrated (we say have global reference frame), in a relationship which can bring to random outcomes. This means, for observing the non-classical correlations, the devices must have that calibration in previous. However, that calibration can’t always be guaranteed in reality due to unintentional flaws or failures of the quantum apparatuses, thus the devices do not always occur the wanted non-classical correlations. In this paper, we show there will always have non-classical correlations by the proper operations, when the devices have local reference. The quantity of true randomness in the observed non-classical correlations is then quantified by the violation values of some inequality. Besides we also consider the devices without local reference and show the probability of non-classical correlations occurring in 100 trials.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Notes

  1. Alice has three vectors \(l_{1},l_{2},l_{3}\) and Bob has three vectors \(a_{1},a_{2},a_{3}\). Alice and Bob each choose two vectors can form an inequality like Eq. (7). A total of nine CHSH-like inequalities are formed.

References

  1. Brunner, N., Pironio, S., Acín, A.: Testing the dimension of Hilbert spaces. Phys. Rev. Lett. 100, 210503 (2008)

    Article  ADS  MathSciNet  Google Scholar 

  2. Wehner, S., Christandl, M., Doherty, A.C.: Lower bound on the dimension of a quantum system given measured data. Phys. Rev. A 78, 062112 (2008)

    Article  ADS  Google Scholar 

  3. Ambainis, A., Nayak, A., Ta-Shma, A.: Dense quantum coding and quantum finite automata. J. ACM 49, 496–511 (2002)

    Article  MathSciNet  Google Scholar 

  4. Ambainis, A., Leung, D., Mancinska, L., et al.: Quantum random access codes with shared randomness. arXiv: 0810.2937 (2008)

  5. Hayashi, M., Iwama, K., Nishimura, H.: (4, 1) Quantum random access coding does not exist-one qubit is not enough to recover one of four bits. N. J. Phys. 8, 129 (2006)

    Article  Google Scholar 

  6. Chaturvedi, A., Pawłowski, M., Horodecki, K.: Random access codes and nonlocal resources. Phys. Rev. A 96(2), 022125 (2017)

    Article  ADS  Google Scholar 

  7. Pawłowski, M., Źukowski, M.: Entanglement-assisted random access codes. Phys. Rev. A 81, 042326 (2010)

    Article  ADS  Google Scholar 

  8. Dall’Arno, M., Passaro, E., Gallego, R., Acín, A.: Robustness of device-independent dimension witnesses. Phys. Rev. A 86(4), 042312 (2012)

    Article  ADS  Google Scholar 

  9. Gallego, R., Brunner, N., Hadley, C., Acín, A.: Device-independent tests of classical and quantum dimensions. Phys. Rev. Lett. 105(23), 230501 (2010)

    Article  ADS  Google Scholar 

  10. Li, H.W., Yin, Z.Q., Wu, Y.C., et al.: Semi-device-independent random-number expansion without entanglement. Phys. Rev. A 84, 034301 (2011)

    Article  ADS  Google Scholar 

  11. Mironowicz, P., Li, H.W., Pawłowski, M.: Properties of dimension witnesses and their semidefinite programming relaxations. Phys. Rev. A 90, 022322 (2014)

    Article  ADS  Google Scholar 

  12. Li, H.W., Pawłowski, M., Yin, Z.Q., et al.: Semi-device-independent randomness certification using n\(\rightarrow \)1 quantum random access codes. Phys. Rev. A 85, 052308 (2012)

    Article  ADS  Google Scholar 

  13. Wang, Y.K., Qin, S.J., Song, T.T., et al.: Effects of relaxed assumptions on semi-device-independent randomness expansion. Phys. Rev. A 89, 032312 (2014)

    Article  ADS  Google Scholar 

  14. Wang, Y.K., Qin, S.J., Wu, X., Gao, F., Wen, Q.Y.: Reduced gap between observed and certified randomness for semi-device-independent protocols. Phys. Rev. A 92, 052321 (2015)

    Article  ADS  Google Scholar 

  15. Li, H.W., Mironowicz, P., Pawłowski, M., et al.: Relationship between semi-and fully-device-independent protocols. Phys. Rev. A 87, 020302 (2013)

    Article  ADS  Google Scholar 

  16. Bartlett, S.D., Rudolph, T., Spekkens, R.W.: Reference frames, superselection rules, and quantum information. Rev. Mod. Phys. 79, 555 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  17. Costa, F., Harrigan, N., Rudolph, T., Brukner, C.: Entanglement detection with bounded reference frames. N. J. Phys. 11(12), 123007 (2009)

    Article  MathSciNet  Google Scholar 

  18. Shadbolt, P., et al.: Guaranteed violation of a Bell inequality without aligned reference frames or calibrated devices. Sci. Rep. 2, 470 (2012)

    Article  Google Scholar 

  19. Mayers, D., Yao, A.C.C.: Proceedings of the 39th Annual Symposium on Foundations of Computer Science, pp. 503–509 (1998)

  20. Clauser, J.F., Horne, M.A., Shimony, A., et al.: Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880884 (1969)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work is supported by National Natural Science Foundation of China (Grant Nos. 61672110 and 61671082).

Author information

Authors and Affiliations

  1. State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    S.-J. Qin, Y.-K. Wang, R.-Z. Li, F. Gao & Q.-Y. Wen

  2. State Key Laboratory of Cryptology, P.O. Box 5159, Beijing, 100878, China

    S.-J. Qin

Authors
  1. S.-J. Qin
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Y.-K. Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. R.-Z. Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. F. Gao
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Q.-Y. Wen
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to S.-J. Qin.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qin, SJ., Wang, YK., Li, RZ. et al. The randomness in 2\(\rightarrow \)1 quantum random access code without a shared reference frame. Quantum Inf Process 17, 276 (2018). https://doi.org/10.1007/s11128-018-2040-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-018-2040-5

Keywords