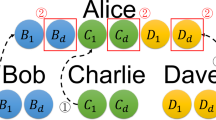Skip to main content
Springer Nature Link
Log in

Limited resource semiquantum secret sharing

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

A Comment to this article was published on 24 June 2020

Abstract

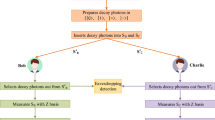
The idea of semiquantum secret sharing (SQSS) is that quantum Alice wants to share secret information with clients such as Bob and Charlie who have limited quantum capability. Neither Bob nor Charlie can reconstruct the secret information unless they collaborate together. In existing semiquantum secret sharing protocols, clients generally need the ability of quantum measurement in classical basis and quantum parties usually need to access quantum memory. In this paper, we propose a relatively efficient SQSS protocol where limited Bob and Charlie can realize secret sharing without making any measurements and quantum Alice does not have to access quantum memory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Shamir, A.: How to share a secret. Commun. ACM 22(11), 612–613 (1979)

    Article  MathSciNet  Google Scholar 

  2. Blakley, G.R.: Safeguarding cryptographic keys. Proc. National Comput. Conf. 48, 313–317 (1979)

    Google Scholar 

  3. Gruska, J., Gruska, J.: Foundations of Computing. International Thomson Computer Press Boston, MA (1997)

    MATH  Google Scholar 

  4. Greenberger, D.M., Horne, M.A., Shimony, A., Zeilinger, A.: Bell’s theorem without inequalities. Am. J. Phys. 58(12), 1131–1143 (1990)

    Article  ADS  MathSciNet  Google Scholar 

  5. Hillery, M., Bužek, V., Berthiaume, A.: Quantum secret sharing. Phys. Rev. A 59(3), 1829 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  6. Guo, G.P., Guo, G.C.: Quantum secret sharing without entanglement. Phys. Lett. A 310(4), 247–251 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  7. Xiao, L., Long, G.L., Deng, F.G., Pan, J.W.: Efficient multiparty quantum-secret-sharing schemes. Phys. Rev. A 69(5), 052307 (2004)

    Article  ADS  Google Scholar 

  8. Yan, F.L., Gao, T.: Quantum secret sharing between multiparty and multiparty without entanglement. Phys. Rev. A 72(1), 012304 (2005)

    Article  ADS  Google Scholar 

  9. Markham, D., Sanders, B.C.: Graph states for quantum secret sharing. Phys. Rev. A 78(4), 042309 (2008)

    Article  ADS  MathSciNet  Google Scholar 

  10. Bell, B., Markham, D., Herrera-Martí, D., Marin, A., Wadsworth, W., Rarity, J., Tame, M.: Experimental demonstration of graph-state quantum secret sharing (2014) arXiv preprint arXiv:1411.5827

  11. Wang, M., Wang, W., Chen, J., Farouk, A.: Secret sharing of a known arbitrary quantum state with noisy environment. Quantum Inf. Process. 14(11), 4211–4224 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  12. Zhu, Z., Hu, A., Fu, A.: Cryptanalysis of a new circular quantum secret sharing protocol for remote agents. Quantum Inf. Process. 12(2), 1173–1183 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  13. Qin, S., Gao, F., Wen, Q., Zhu, F.: Cryptanalysis of the Hillery–Buzek–Berthiaume quantum secret-sharing protocol. Phys. Rev. A 76(6), 062324 (2007)

    Article  ADS  Google Scholar 

  14. Long, Y., Qiu, D., Long, D.: Quantum secret sharing of multi-bits by an entangled six-qubit state. J. Phys. A 45(19), 195303 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  15. Jia, H., Wen, Q., Gao, F., Qin, S., Guo, F.: Dynamic quantum secret sharing. Phys. Lett. A 376(10), 1035–1041 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  16. Liu, Z., Chen, H., Xu, J., Liu, W., Li, Z.: High-dimensional deterministic multiparty quantum secret sharing without unitary operations. Quantum Inf. Process. 11(6), 1785–1795 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  17. Wu, Y., Cai, R., He, G., Zhang, J.: Quantum secret sharing with continuous variable graph state. Quantum Inf. Process. 13(5), 1085–1102 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  18. Qin, H., Dai, Y.: Efficient quantum secret sharing. Quantum Inf. Process. 15(5), 2091–2100 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  19. Wu, Y., Zhou, J., Gong, X., Guo, Y., Zhang, Z., He, G.: Continuous-variable measurement-device-independent multipartite quantum communication. Phys. Rev. A 93(2), 022325 (2016)

    Article  ADS  Google Scholar 

  20. Qin, H., Zhu, X., Dai, Y.: (t, n) Threshold quantum secret sharing using the phase shift operation. Quantum Inf. Process. 14(8), 2997–3004 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  21. Song, X., Liu, Y.: Cryptanalysis and improvement of verifiable quantum (k, n) secret sharing. Quantum Inf. Process. 15(2), 851–868 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  22. Huang, W., Wen, Q.Y., Liu, B., Gao, F., Sun, Y.: Robust and efficient quantum private comparison of equality with collective detection over collective-noise channels. Sci. China Phys. Mech. Astron. 56(9), 1670–1678 (2013)

    Article  ADS  Google Scholar 

  23. Gao, F., Liu, B., Huang, W., Wen, Q.Y.: Postprocessing of the oblivious key in quantum private query. IEEE J. Sel. Topics Quantum Electron. 21(3), 98–108 (2015)

    Article  ADS  Google Scholar 

  24. Jia, H.Y., Wen, Q.Y., Song, T.T., Gao, F.: Quantum protocol for millionaire problem. Opt. Commun. 284(1), 545–549 (2011)

    Article  ADS  Google Scholar 

  25. Li, Q., Li, Z., Chan, W.H., Zhang, S., Liu, C.: Blind quantum computation with identity authentication. Phys. Lett. A 382(14), 938–941 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  26. Huang, W., Wen, Q.Y., Liu, B., Su, Q., Qin, S.J., Gao, F.: Quantum anonymous ranking. Phys. Rev. A 89(3), 032325 (2014)

    Article  ADS  Google Scholar 

  27. Wang, Q., Yu, C., Gao, F., Qi, H., Wen, Q.Y.: Self-tallying quantum anonymous voting. Phys. Rev. A 94(2), 022333 (2016)

    Article  ADS  Google Scholar 

  28. Boyer, M., Kenigsberg, D., Mor, T.: Quantum key distribution with classical Bob. Phys. Rev. A 99(14), 140501 (2007)

    MathSciNet  MATH  Google Scholar 

  29. Li, Q., Chan, W.H., Zhang, S.: Quantum key distribution with classical Bob. Sci. Rep. 6(1), 19898 (2016)

    Article  ADS  Google Scholar 

  30. Li, Q., Chan, W.H., Long, D.Y.: Semiquantum secret sharing using entangled states. Phys. Rev. A 82(2), 022303 (2010)

    Article  ADS  Google Scholar 

  31. Wang, J., Zhang, S., Zhang, Q., Tang, C.J.: Semiquantum secret sharing using two-particle entangled state. Int. J. Quantum Inf. 10(05), 1250050 (2012)

    Article  MathSciNet  Google Scholar 

  32. Li, L., Qiu, D., Mateus, P.: Quantum secret sharing with classical Bobs. J. Phys. A: Math. Theor. 46(4), 045304 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  33. Xie, C., Li, L., Qiu, D.: A novel semi-quantum secret sharing scheme of specific bits. Int. J. Theor. Phys. 54(10), 3819–3824 (2015)

    Article  MathSciNet  Google Scholar 

  34. Yin, A., Wang, Z., Fu, F.: A novel semi-quantum secret sharing scheme based on Bell states. Mod. Phys. Lett. B 31, 1750150 (2017)

    Article  ADS  Google Scholar 

  35. Gao, X., Zhang, S., Chang, Y.: Cryptanalysis and improvement of the semi-quantum secret sharing protocol. Int. J. Theor. Phys. 56, 1–9 (2017)

    Article  Google Scholar 

  36. Sun, Z.W., Du, R.G., Long, D.Y.: Quantum key distribution with limited classical bob. Int. J. Quantum Inf. 11(01), 1350005 (2013)

    Article  MathSciNet  Google Scholar 

  37. He, J., Li, Q., Wu, C., Chan, W.H., Zhang, S.: Measurement-device-independent semiquantum key distribution. Int. J. Quantum Inf. 16(2), 1850012 (2018)

    Article  Google Scholar 

  38. Yang, C.W., Hwang, T.: Efficient key construction on semi-quantum secret sharing protocols. Int. J. Quantum Inf. 11(5), 1350052 (2013)

    Article  MathSciNet  Google Scholar 

  39. Hwang, W.Y.: Quantum key distribution with high loss: toward global secure communication. Phys. Rev. Lett. 91(5), 057901 (2003)

    Article  ADS  Google Scholar 

  40. Lo, H.K., Ma, X., Chen, K.: Decoy state quantum key distribution. Phys. Rev. Lett. 94(23), 230504 (2005)

    Article  ADS  Google Scholar 

  41. Wang, X.B.: Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94(23), 230503 (2005)

    Article  ADS  Google Scholar 

  42. Ma, X., Qi, B., Zhao, Y., Lo, H.K.: Practical decoy state for quantum key distribution. Phys. Rev. A 72(1), 012326 (2005)

    Article  ADS  Google Scholar 

  43. Brassard, G., Lütkenhaus, N., Mor, T., Sanders, B.C.: Limitations on practical quantum cryptography. Phys. Rev. Lett. 85(6), 1330 (2000)

    Article  ADS  Google Scholar 

  44. Deutsch, D., Ekert, A., Jozsa, R., Macchiavello, C., Popescu, S., Sanpera, A.: Quantum privacy amplification and the security of quantum cryptography over noisy channels. Phys. Rev. Lett. 77(13), 2818 (1996)

    Article  ADS  Google Scholar 

  45. Bennett, C.H., Brassard, G., Crépeau, C., Maurer, U.M.: Generalized privacy amplification. IEEE Trans. Inf. Theory 41(6), 1915–1923 (1995)

    Article  MathSciNet  Google Scholar 

  46. Krawec, W.O., Geiss, E.P.: Limited resource semi-quantum key distribution (2017) arXiv preprint arXiv:1710.05076

  47. Rosenberg, D., Harrington, J.W., Rice, P.R., Hiskett, P.A., Peterson, C.G., Hughes, R.J., Lita, A.E., Nam, S.W., Nordholt, J.E.: Long-distance decoy-state quantum key distribution in optical fiber. Phys. Rev. Lett. 98(1), 010503 (2007)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the Joint Funds of the National Natural Science Foundation of China and China General Technology Research Institute (Grant No. U1736113), the National Natural Science Foundation of China (Grant No. 61772565), and the Hunan Provincial Natural Science Foundation of China (Grant No. 2018JJ2403).

Author information

Authors and Affiliations

  1. College of Information Engineering, Xiangtan University, Xiangtan, 411105, China

    Zhulin Li

  2. Key Laboratory of Hunan Province for Internet of Things and Information Security, College of Information Engineering, Xiangtan University, Xiangtan, 411105, China

    Qin Li

  3. China General Technology Research Institute, Beijing, 100091, China

    Chengdong Liu & Yu Peng

  4. Department of Mathematics and Information Technology, The Education University of Hong Kong, Ting Kok, Hong Kong

    Wai Hong Chan

  5. Department of Computer Science, Sun Yat-sen University, Guangzhou, 510006, China

    Lvzhou Li

Authors
  1. Zhulin Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Qin Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Chengdong Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yu Peng
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Wai Hong Chan
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Lvzhou Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Qin Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Z., Li, Q., Liu, C. et al. Limited resource semiquantum secret sharing. Quantum Inf Process 17, 285 (2018). https://doi.org/10.1007/s11128-018-2058-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-018-2058-8

Keywords